Основные виды выборки, способы отбора
В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения.
Основным условием проведения выборочного обследования является предупреждение возникновения систематических (тенденциозных) ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности.
Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности.
Практика применения выборочного метода в экономико-статистических исследованиях использует следующие способы отбора единиц из генеральной совокупности:
1) индивидуальный отбор - в выборку отбираются отдельные единицы;
2) групповой отбор - в выборку попадают качественно однородные группы или серии изучаемых единиц;
3) комбинированный отбор как комбинация индивидуального и группового отбора.
Способы отбора определяются правилами формирования выборочной совокупности.
Способы отбора определяются правилами формирования выборочной совокупности.
Выборка может быть:
— собственно-случайная;
— механическая;
— типическая;
— серийная;
— комбинированная.
Собственно-случайная выборка состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки.
Доля выборки есть отношение числа единиц выборочной совокупности n к численности единиц генеральной совокупности N, т.е.
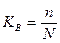 .
.
Так, при 5%-ной выборке из партии товара в 2 000 ед. численность выборки n составляет 100 ед. (5*2000:100), а при 20%-ной выборке она составит 400 ед. (20*2000:100) и т.д.
Механическая выборка состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки.
Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке — каждая 20-я единица (1:0,05) и т.д.
Таким образом, в соответствии с принятой долей отбора, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица.
Важной особенностью механической выборки является то, что формирование выборочной совокупности можно осуществить, не прибегая к составлению списков. На практике часто используют тот порядок, в котором фактически размещаются единицы генеральной совокупности. Например, последовательность выхода готовых изделий с конвейера или поточной линии, порядок размещения единиц партии товара при хранении, транспортировке, реализации и т.д.
Типическая выборка.При типической выборке генеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.
Типическая выборка обычно применяется при изучении сложных статистических совокупностей. Например, при выборочном обследовании производительности труда работников торговли, состоящих из отдельных групп по квалификации.
Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность.
Для определения средней ошибки типической выборки используются формулы:
повторный отбор
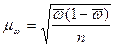 ,
, 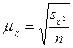
бесповторный отбор
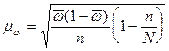 ,
, 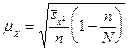
Дисперсия определяется по следующим формулам:
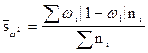 ,
, 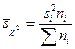
Пример.
Для выявления доли простоев из-за несвоевременного поступления полуфабрикатов была проведена фотография рабочего дня 10% рабочих четырех различных цехов. Отбор рабочих внутри цехов производится методом механического отбора. В результате выборки были получены следующие данные:
| Цех | Число рабочих в выборке | Удельный вес простоев из-за несвоевременного поступления полуфабрикатов, % |
| №1 | ||
| №2 | ||
| №3 | ||
| №4 |
С вероятностью 0,954 требуется определить пределы, в которых находится доля простоев на заводе из-за несвоевременного поступления полуфабрикатов.
Рассчитаем долю простоев из-за несвоевременного поступления полуфабрикатов в выборке:
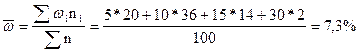
Рассчитаем дисперсии типических групп:
для группы 
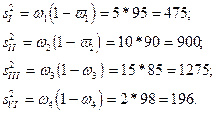
Средняя из внутригрупповых дисперсий определяется по формуле:
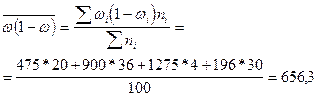
Определяем среднюю ошибку в выборочной доле:
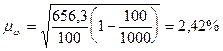
Рассчитаем предельную ошибку выборки для доли с вероятностью 0,954:
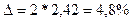
С вероятностью 0,954 можно утверждать, что доля простоев рабочих из-за несвоевременного поступления полуфабрикатов находится в пределах 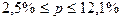 .
.
Серийная выборка. При серийной выборке генеральную совокупность делят на одинаковые по объему группы — серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию.
При бесповторном отборе серий средняя ошибка выборочной серии определяется по формуле:
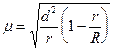 ,
,
где 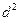 — межсерийная дисперсия средних;
— межсерийная дисперсия средних;
R — число серий в генеральной совокупности;
r — число отобранных серий.
Пример.
В механическом цехе завода в десяти бригадах работает 100 рабочих. В целях изучения квалификации рабочих была произведена 20%-ная серийная бесповторная выборка, в которую вошли 2 бригады. Получено следующее распределение обследованных рабочих по разрядам:
| Рабочие | Разряды рабочих в бригаде 1 | Разряды рабочих в бригаде 2 |
Необходимо определить с вероятностью 0,997 пределы, в которых находится средний разряд рабочих механического цеха.
Определим выборочные средние по бригадам и общую среднюю:
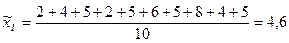
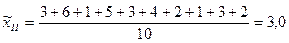
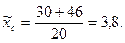
Определим межсерийную дисперсию:
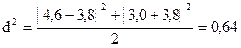
Рассчитаем среднюю ошибку выборки:
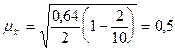
Вычислим предельную ошибку выборки с вероятностью 0,997.
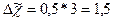
С вероятностью 0,997 можно утверждать, что средний разряд рабочих механического цеха находится в пределах 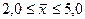 .
.
При бесповторном серийном отборе средняя ошибка выборки для доли определятся по формуле:
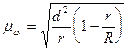 ,
,
где 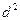 — межсерийная дисперсия доли.
— межсерийная дисперсия доли.
Пример.
200 ящиков деталей упакованы по 40 шт. в каждом. Для проверки качества деталей был проведён сплошной контроль деталей в 20 ящиках (выборка бесповторная). В результате контроля установлено, что доля бракованных деталей составляет 15%. Межсерийная дисперсия равна 49. С вероятностью 0,997 определим пределы, в которых находится доля бракованной продукции в партии ящиков.
Определим среднюю ошибку выборки для доли:
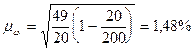 .
.
Предельная ошибка выборки для доли с вероятностью 0,997 равна: 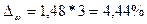 .
.
С вероятностью 0,997 можно утверждать, что доля бракованных деталей в партии будет находиться в пределах от 10,59% до 19,41%.
В статистике различают одноступенчатые и многоступенчатые способы отбора единиц в выборочную совокупность.
При одноступенчатой выборке каждая отобранная единица сразу же подвергается изучению по заданному признаку. Так обстоит дело при собственно-случайной и серийной выборке.
При многоступенчатой выборке производят подбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы. Так производится типическая выборка с механическим способом отбора единиц в выборочную совокупность.
Комбинированная выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц.
Малая выборка
При контроле качества товаров в экономических исследованиях эксперимент может проводиться на основе малой выборки.
Под малой выборкой понимается несплошное статистическое обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Объем малой выборки обычно не превышает 30 единиц и может доходить до 4 — 5 единиц.
Средняя ошибка малой выборки 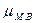 вычисляется по формуле:
вычисляется по формуле:
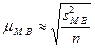 ,
,
где 
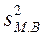 — дисперсия малой выборки.
— дисперсия малой выборки.
При определении дисперсии 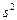 число степеней свободы равно n-1:
число степеней свободы равно n-1:
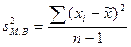 .
.
Предельная ошибка малой выборки 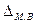 определяется по формуле
определяется по формуле 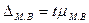
При этом значение коэффициента доверия t зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n. Для отдельных значений t и n доверительная вероятность малой выборки определяется по специальным таблицам Стьюдента, в которых даны распределения стандартизированных отклонений:
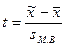 .
.
| n | t | ||||
| 0,5 | 1,0 | 1,5 | 2,0 | 3,0 | |
| 0,347 | 0,609 | 0,769 | 0,861 | 0,942 | |
| 0,362 | 0,637 | 0,806 | 0,898 | 0,970 | |
| 0,368 | 0,649 | 0,823 | 0,914 | 0,980 | |
| 0,371 | 0,657 | 0,832 | 0,923 | 0,985 | |
| 0,376 | 0,666 | 0,846 | 0,936 | 0,992 | |
| 0,377 | 0,670 | 0,850 | 0,940 | 0,993 |
Поскольку при проведении малой выборки в качестве доверительной вероятности практически принимается значение 0,59 или 0,99, то для определения предельной ошибки малой выборки 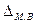 используются следующие показания распределения Стьюдента
используются следующие показания распределения Стьюдента
| n | 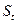
| |
| 0,95 | 0,99 | |
| 3,183 | 5,841 | |
| 2,777 | 4,604 | |
| 2,571 | 4,032 | |
| 2,447 | 3,707 | |
| 2,364 | 3,500 | |
| 2,307 | 3,356 | |
| 2,263 | 3,250 | |
| 2,119 | 2,921 | |
| 2,078 | 2,832 |
Пример.
При контрольной проверке качества поставленной в торговлю колбасы получены данные о содержании поваренной соли в пробах. По данным выборочного обследования нужно установить с вероятностью 0,95 предел, в котором находится средний процент содержания поваренной соли в данной партии товара.
Составляем расчётную таблицу и по её итогам определяем среднюю пробу малой выборки.
Пробы 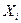
| 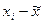
| 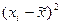
|
| 4,3 | 0,2 | 0,04 |
| 4,2 | 0,1 | 0,01 |
| 3,8 | 0,3 | 0,09 |
| 4,3 | 0,2 | 0,04 |
| 3,7 | - 0,4 | 0,16 |
| 3,9 | - 0,2 | 0,04 |
| 4,5 | 0,4 | 0,16 |
| 4,4 | 0,3 | 0,09 |
| 4,0 | - 0,1 | 0,01 |
| 3,9 | - 0,2 | 0,04 |
 41,0 41,0
| — | 0,68 |
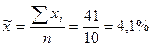
Определяем дисперсию малой выборки:
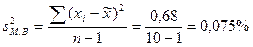
Определяем среднюю ошибку малой выборки:
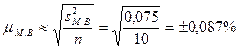
Исходя из численности выборки (n=10) и заданной вероятности 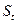 =0,95, устанавливается по распределению Стьюдента значение коэффициента доверия t=2,263.
=0,95, устанавливается по распределению Стьюдента значение коэффициента доверия t=2,263.
Предельная ошибка малой выборки составит:
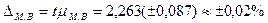
Следовательно, с вероятностью 0,95 можно утверждать, что во всей партии колбасы содержание поваренной соли находится в пределах:
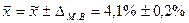 , т.е. от 4,1% - 0,2%=3,9%
, т.е. от 4,1% - 0,2%=3,9%
до 4,1%+0,2%=4,3%.
Вопросы для самоконтроля
1. В чем заключаются особенности и каково значение выборочного наблюдения?
2. Что такое генеральная и выборочная совокупности?
3. Что такое ошибка выборочного наблюдения, по какой формуле она исчисляется и от каких факторов зависит ее величина?
4. Что такое повторная и бесповторная выборка? Какая из них точнее?
5. Чем отличается предельная ошибка выборки от средней?
6. Как определяется необходимая численность выборки при заданной ее точности?
7. Чем отличается случайный отбор от механического?
8. Как организуется типический отбор и в чем его преимущества?
9. Как организуется серийный (гнездовой) отбор и в каких случаях он применяется?
10. Какие имеются способы распространения выборочных данных?
11. Как оцениваются ошибки малой выборки?
Дата добавления: 2017-04-20; просмотров: 2790;
