Экспериментальное определение электропроводности.

Значение электропроводности нельзя определять аналогично тому, как она определяется в проводниках первого рода (металлах). Связано это с тем, что необходимо создавать условия, при которых gradm_i = 0. Это обусловлено наличием градиента химического потенциала, который обязательно вызовет дополнительную диффузию ионов, не связанную с электропроводностью. Поэтому для экспериментального измерения электропроводности используется переменный ток при частоте от 1 кГц и выше. Диффузией при измерениях электропроводимости можно пренебречь, если использовать мостовую схему, приведённую на рисунке 6.1.

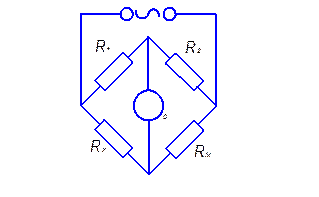
Рис. 6.1 Схема моста переменного тока.

В состоянии баланса (при отсутствии напряжения на нуль – индикаторе) выполняется соотношение .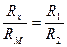

Состояние баланса достигается варьированием сопротивлением R_M при постоянных значениях R₁ и R₂ (R_x –это сопротивление исследуемого электролита). Как и для обычных металлических проводников, сопротивление растворов можно рассчитать по формуле:

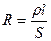, (6.9)

r - удельное сопротивление материала; l – длина проводника; S – площадь поперечного сечения. В случае измерения электропроводности растворов S – площадь электродов, а l расстояние между ними (рис. 6.2).

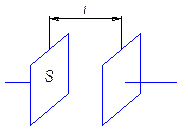
Рис. 6.2 Схема ячейки для измерения электропроводности

Таким образом, определив значение R_xпо данной схеме и используя уравнение (6.9), можно рассчитать величину удельного сопротивления электролита. Обычно в справочниках приводится обратная величина k - удельная электропроводимость электролита.

.

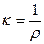(6.10)

Из (6.9) и (6.10) получаем:

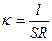(6.11)

Размерность удельной электропроводности Ом^-1×см^-1 или См×м^-1 (См – сименс).

Удельная электропроводность – это электропроводимость раствора, заключённого между двумя параллельными электродами, имеющими площадь 1м² и расположенными на расстоянии 1м друг от друга.

Если с использованием схемы, приведённой на рис. 6.1, определить удельные электропро­­водности различных растворов в зависимости от их концентрации, то можно наблюдать следующую зависимость (рис. 6.3).

При максимальном разбавлении растворавеличина его удельной электропроводности стремится к удельной электропроводности чистой воды (~ 10^-5 См/м).

Как видно из рисунка 6.3 зависимость электропроводности от концентрации, как правило, имеет максимум. Вследствие ион – ионного взаимодействия ее величина снижается при высоких концентрациях. Наличие такой аномальной зависимости делает неудобным использование величин удельной электропроводности, поэтому целесообразно ввести понятие эквивалентной электропроводности, которое обозначается буквой l и определяется соотношением:

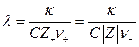(6.12)

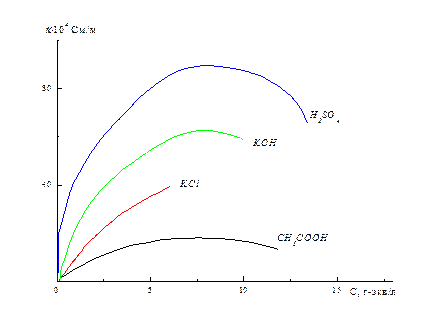
Рис. 6.3 Зависимость удельной электропроводности от концентрации растворов.

Согласно (6.12) эквивалентная электропроводность является удельной электропроводностью отнесенной к единице концентрации раствора. Она представляет собой электропроводность объёма электролита, содержащего 1г - эквивалент растворённого вещества, находящегося между двумя параллельными электродами, расположенными на расстоянии 1м друг от друга (размерность м ²/Ом×г - экв.).

Если бы потоки миграции не зависели от ион – ионного взаимодействия, то l сохраняло бы постоянство при всех концентрациях. Однако при высоких концентрациях эквивалентная электропроводность не постоянна (рис. 6.4). При бесконечном разбавлении раствора,она стремится к своему постоянному значению.

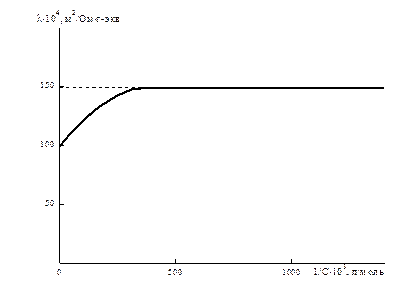
Рис. 6.4 Зависимость эквивалентной электропроводности от разбавления.

Существует связь между эквивалентной электропроводностью l и абсолютной скоростью движения ионов U_i.

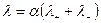, (6.13)

где a - степень диссоциации и 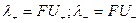, а U₊, U_- - абсолютные подвижности катиона и аниона.

Величины l₊ и l_- носят названия подвижностей ионов. Для сильных электролитов (a = 1):

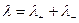(6.14)

При бесконечном разбавлении:

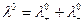, (6.15)

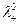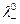где и - предельные подвижности ионов.

Таблица 6.1

Предельные подвижности ионов в воде при различных температурах.

Ион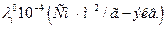
0°С	18°С	25°С	45°С	100°С
Li+ Na+ K+ [(CH3)4N]+ [(C2H5)4N]+	19,4 26,5 40,7 24,4 16,4	32,8 42,8 63,9 28,2	38,7 50,1 73,5 44,9 32,7	73,7 103,5 - -	- -
F– Cl– Br– I- CH3COO-	- 42,6 41,4 20,1	47,3 66,5	65,4 76,4 76,8 40,9	- 108,9 110,7 108,6 -	- - - -

Из приведенных в таблице 6.1 значений подвижностей ионов следует, что наблюдается:

1. увеличение подвижности ионов с увеличением температуры (в отличие от металлов);

2. увеличение подвижности ионов с ростом кристаллографических радиусов ионов, однако, разветвленное строение иона приводит к ее снижению.

Противоречие между увеличением подвижности иона и величиной его кристаллографического радиуса чисто кажущееся. Если рассматривать поведение гидратированного иона по аналогии с шаром в жидкости, то согласно закону Стокса скорость его движения обратно пропорциональна радиусу

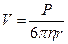, (6.16)

где P – давление;h - динамическая вязкость и r – радиус шара.

Кроме того, чем меньше радиус иона, тем большее поле он создаёт, а, следовательно, больше гидратирован. Таким образом, совместное влияние уравнения (6.16) и гидратации иона имеет в качестве своего следствия наличие максимальной электропроводности у ионов большего кристаллографического радиуса. Для многих растворов характерно эмпирическое правило Вальдена – Писаржевского.

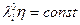(6.17)