Вариация количественного и качественного признаков.
Если один из взаимосвязанных признаков количественный, а второй - качественный, то тесноту связи в данном случае можно определить на основе дисерийного коэффициента (ri):
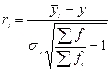 (18),
(18),
где y – среднее значение признака;
σy – среднее квадратическое отклонение;
f – частота.
Для подтверждения связи между признаками достаточно, чтобы дисерийный коэффициент был больше 0,3 (по модулю). Исходные данные для соответствующего расчета тесноты связи между признаками приведены в таблице 2.5.
Таблица 2.5 - Оценка потребителями взаимосвязи качества продукции с ростом цен
| Изменение качества продукции по мнению потребителей | Темпы роста цен за месяц | Всего | ||||
| 100-102 (101) | 102-104 (103) | 104-106 (105) | 106-108 (107) | 108-110 (109) | ||
| Качество улучшается (f1) | ||||||
| Качество не улучшается (f2) | ||||||
| Всего (f) |
Рассчитаем средние темпы роста цен для двух групп и совокупности в целом.
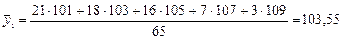
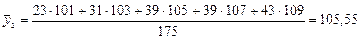
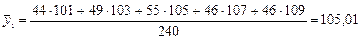
Среднее квадратическое отклонение для сгруппированного ряда определяется по формуле 19:
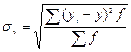 (19)
(19)
σy =  = 2,75
= 2,75
Таким образом,
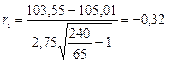

Сумма дисерийных коэффициентов должна быть равна нулю. Отрицательное значение r1 означает, что с ростом цен качество продукции не улучшается. Этот вывод подтверждается положительным расчётным значением r2 .
Дата добавления: 2017-01-29; просмотров: 652;
