Вариация количественных признаков
А) Взаимосвязь между двумя ранжированными рядами переменных.
Задача оценки взаимосвязи между проранжированными переменными возникает всякий раз, когда проводится маркетинговое исследование на основе субъективных оценок специалистов в данной области. Например, необходимо установить, существует ли взаимосвязь между рангами компании, присвоенными по качеству производимой ею продукции, и по положению компании на рынке (ранг может присваиваться по рыночной доле, принадлежащей компании). Для анализа были собраны необходимые данные по 12 компаниям (таблица 2.6).
Таблица 2.6 - Имидж качества продукции компании и её место на рынке
(по доле, занимаемой компанией)
| Компания | Ранг качества продукции (Х) | Ранг рыночной доли (Y) | Разность рангов (Δi) | Квадрат разности рангов (Δi2) |
| A | ||||
| B | -1 | |||
| C | ||||
| D | ||||
| E | -1 | |||
| F | -1 | |||
| G | -1 | |||
| H | -4 | |||
| I | ||||
| J | ||||
| K | -1 | |||
| L | ||||
| Сумма |
Для определения тесноты связи между проранжированными признаками рассчитаем коэффициент корреляции рангов Спирмэна (R):
 (20),
(20),
где Δi - разница рангов по двум переменным;
n - число ранжированных позиций.
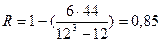
Границы коэффициента корреляции от –1 до +1. Чем ближе модуль значения коэффициента к 1, тем теснее связь между признаками. Однако в статистической практике широко применяется проверка коэффициента корреляции рангов на значимость. При этом используется t-распределение Стьюдента:
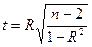 (21)
(21)
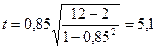
Расчётное значение t-критерия сравнивается с табличным значением tтабл. (для уровня значимости р = 0,05 и числа степеней свободы n - 1 = 10) = 2,228. Если t расчётное больше, чем табличное, то коэффициент корреляции рангов считается значимым. Следовательно, существует взаимосвязь между качеством выпускаемой фирмой продукции и её местом на рынке.
Б) Взаимосвязь между двумя количественными переменными
Теснота связи и ее направление между двумя количественными переменными определяются путем расчета коэффициента корреляции, который изменяется от -1 до + 1. Абсолютная величина корреляции характеризует тесноту связи, а знак указывает на её направление. Коэффициент корреляции определяется по формуле (22):
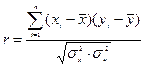 (22),
(22),
где среднее квадратическое отклонение 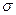 рассчитывается по формулам (23 и 24):
рассчитывается по формулам (23 и 24):
 (23);
(23);
 (24).
(24).
Список использованных источников:
- Завойская И.В., Лимарева Ю.А. Маркетинг [Электронный ресурс]: практикум. ФГБОУ ВПО «МГТУ», 2013.
- Лимарев П.В., Кучмий Т.И. Маркетинговые исследования: конспект лекций: учебное пособие. Магнитогорск: ЗАО «Магнитогорский Дом Печати», 2012. – 76 с.
3. Анализ временных рядов и прогнозирование: уч. пособие/ М.В. Бушманова, Т.А. Иванова, Г.Г. Мельникова и др. – Магнитогорск: МГТУ, 2006.
4. Березин И. С. Маркетинговые исследования. Как это делают в России. – М.: Вершина, 2005.
5. Голубков Е.П. Маркетинговые исследования: теория, методология и практика.– 3-е изд. М.: Финпресс, 2003
6. Соловьёва Д. Экспертные методы в маркетинге [Электронный ресурс] Режим доступа: http://www.iteam.ru/publications/marketing/.
7. Электронные учебные материалы по курсу «Маркетинговые исследования»: курс лекций / составитель Бушуева Л.И. – Сыктывкар: СГУ, 2002
8. Хаг П. Маркетинговые исследования : руководство по планированию, методологии и оценке [Комплект] : пер. с англ. – К.: Знання-Прес, 2005. – 418 с. : ил., табл. + 1 электрон. опт. диск (CD-ROM). - (Европейский маркетинг).
[1] Уровень значимости (р-уровень) – это показатель, находящийся в убывающей зависимости от надёжности результата. Более высокий p-уровень соответствует более низкому уровню доверия к найденной в выборке зависимости между переменными. Именно p-уровень представляет собой вероятность ошибки, связанной с распространением наблюдаемого результата на всю популяцию. Например, p-уровень = 0,05 (т.е. 1/20) показывает, что имеется 5% вероятность, что найденная в выборке связь между переменными является лишь случайной особенностью данной выборки. Иными словами, если данная зависимость в популяции отсутствует, а вы многократно проводили бы подобные эксперименты, то примерно в одном из двадцати повторений эксперимента можно было бы ожидать такой же или более сильной зависимости между переменными. Во многих исследованиях p-уровень 0,05 рассматривается как «приемлемая граница» уровня ошибки.
Дата добавления: 2017-01-29; просмотров: 781;
