Выводной анализ (использование описательной статистики)
Статистический вывод является видом логического анализа, направленного на получение общих заключений обо всей совокупности на основе наблюдений за малой группой единиц данной совокупности
Выводы делаются на основе анализа небольшого количества фактов. Например, если двое знакомых имеют технически сложный продукт одной марки и оба отзываются о нём негативно, то можно сделать вывод о том, что продукт некачественный.
Однако статистический вывод делается по результатам статистического анализа выборочного исследования и направлен на оценку совокупности в целом. В данном случае результаты выборочных исследований являются отправной точкой для получения общих выводов.
При проведении маркетинговых исследований чаще всего используются следующие статистические выводы: оценка параметров и проверка гипотез.
Оценка параметров генеральной совокупности представляет собой процесс определения, исходя из данных о выборке, интервала, в котором находится один из параметров генеральной совокупности, например, среднее значение. Для этого используют следующие статистические показатели: средние величины, среднюю квадратическую ошибку и желаемый уровень доверительности (обычно 95 или 99%).
Средняя квадратическая ошибкаявляется мерой вариации выборочного распределения при теоретическом предположении, что исследовалось множество независимых выборок одной и той же генеральной совокупности. Она определяется по формуле (5):
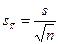 (5),
(5),
где  – средняя квадратическая ошибка выборочной средней,
– средняя квадратическая ошибка выборочной средней,
s – среднее квадратическое отклонение,
n – объём выборки.
Если используются процентные меры, выражающие альтернативную изменчивость качественных признаков, то следует пользоваться формулой (6)
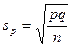 (6),
(6),
где sp – средняя квадратическая ошибка выборочной средней при использовании процентных мер,
p – процент респондентов в выборке, поддержавших первую альтернативу
q = (100 – p) процент респондентов в выборке, поддержавших вторую альтернативу
n – объём выборки.
Из формулы видно, что чем больше вариация, тем больше средняя ошибка, и чем больше объём выборки, тем она меньше.
Поскольку всегда существует выборочная ошибка, необходимо оценить разброс значений изучаемого параметра генеральной совокупности.
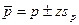 (7).
(7).
Иными словами, чтобы диапазон оценок включал истинную для совокупности оценку, необходимо умножить среднюю квадратичную ошибку на значение нормированного отклонения оценки и добавить полученный результат к значению р (верхний предел) или вычесть его из значения р (нижний предел).
Поскольку производится оценка параметра генеральной совокупности, здесь указывается диапазон, в который попадает истинное значение параметра генеральной совокупности. С этой целью берутся статистическая мера центральной тенденции, величина дисперсии и объём выборки.
Например, 40% жителей Магнитогорска по утрам пьют кофе, доверительный интервал 95%, объём выборки 100 человек:
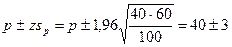
Диапазон оценок, в котором лежит истинная для всей совокупности оценка – 37% - 43%
В ряде случаев делаются суждения относительно какого-либо параметра генеральной совокупности (величине средней, дисперсии, характере распределения, форме и тесноте связи между переменными), исходя из некоторых предположений, размышлений, интуиции, неполных знаний. Такие суждения называются гипотезами.
Статистической гипотезой называется предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки.
Под проверкой гипотезы понимается статистическая процедура, применяемая для подтверждения или отклонения гипотезы, основанная на результатах выборочных исследований. Проверка гипотезы осуществляется на основе выявления согласованности эмпирических данных с гипотетическими. Если расхождение между ними находится в пределах случайных ошибок, гипотезу принимают. При этом не идёт речи о подтверждении правильности гипотезы, а лишь о согласованности данных. Проверка гипотезы проходит в 5 этапов:
1. Делается предположение относительно какой-то характеристики генеральной совокупности, например, о средней величине определённого параметра.
2. Формируется случайная выборка, проводится выборочное исследование и определяются статистические показатели выборки.
3. Сравниваются гипотетическое и статистическое значения исследуемой характеристики.
4. Определяется, соответствуют ли результаты выборочного исследования принятой гипотезе.
5. Если результаты исследования не подтверждают гипотезу, гипотеза пересматривается, поскольку она должна соответствовать данным исследования.
Статистическая проверка гипотезы включает в себя использование выборочного значения характеристики, среднего квадратического отклонения, желательного уровня доверительности и гипотетического значения характеристики для генеральной совокупности в целом. Для проверки гипотез о средних величинах применяется формула:
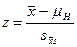 (8),
(8),
где  – средняя для выборки,
– средняя для выборки,
 – гипотетическое значение средней,
– гипотетическое значение средней,
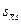 – средняя квадратическая ошибка средней.
– средняя квадратическая ошибка средней.
Пример: предприятие собирается взять на работу грузчика. Предполагаемая его заработная плата составляет 7800 рублей (гипотеза). По результатам исследования, проведенного с целью установления адекватной зарплаты, выяснилось, что среднее квадратическое отклонение составляет 800 рублей, среднее значение в выборке 7950 рублей. Можно ли перенести результаты исследования на всю генеральную совокупность при 95% уровне доверительности и сказать, что гипотеза верна (объем выборки составил 144 человек)?
Подставив значения в формулы 4.8 и 4.5, получим:
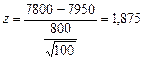
Значение z не превышает табличного для уровня доверительности 95%, следовательно, гипотеза верна.
Расчёты в случае использования процентной меры выглядят следующим образом:
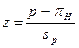 (9),
(9),
где р – процент из выборочного исследования
πН – процент из гипотезы
sp – средняя квадратическая ошибка при расчётах в процентах.
Пример: исходя из собственного опыта один автолюбитель предположил, что ремнями безопасности пользуются 10% автомобилистов (гипотеза). Результаты исследования (1000 респондентов) показали, что ремнями пользуется 80% автомобилистов.
Подставив значения в формулы, получим:
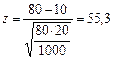
Это значение z значительно превышает табличное, т.е. гипотеза не может быть принята.
Проверка гипотез применяется в тех случаях, когда сложно организовать полномасштабное выборочное исследование и когда требуется сравнить результаты нескольких исследований.
Для проверки гипотез о зависимости между двумя категорийными переменными используется критерий Пирсона (критерий χ2), позволяющий определить насколько значимой является зависимость между двумя переменными. Формулируется нулевая гипотеза, отрицающая наличие между двумя категорийными переменными статистической зависимости. Затем данные исследования (наблюдаемые частоты, hi) табулируются, т.е. строится матрица следующего вида:
Таблица 2.2 – Матрица наблюдаемых частот
| Переменные | ... | i | ∑i | ||
| ... | |||||
| j | |||||
| ∑j | n |
По имеющимся данным определяются ожидаемые частоты fi:
 (10)
(10)
Определив ожидаемые частоты, можем определить величину критерия χ2 и сравнить её с табличной (приложение А):
 (11)
(11)
Пример: зависит ли количество посещений кинотеатра от возраста студентов?
Формируется матрица наблюдаемых частот:
Таблица 5 – Матрица наблюдаемых частот посещений кинотеатра
| Вы ходите в кино? | 1-2 курс | 3-4 курс | 5 курс | Итого |
| Да | ||||
| Нет | ||||
| Итого |
По формуле 14 определяются ожидаемые частоты:
Таблица 6 - Матрица ожидаемых частот посещений кинотеатра
| Вы ходите в кино? | 1-2 курс | 3-4 курс | 5 курс | Итого |
| Да | ||||
| Нет | ||||
| Итого |
По формуле 15 вычисляется критерий χ2
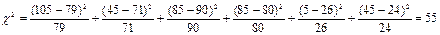
Полученное значение сравниваем с табличным в соответствии с количеством степеней свободы (df) и уровнем значимости[1]. Количество степеней свободы определяется по формуле 12 следующим образом:
df = (кол-во строк – 1) . (кол-во столбцов – 1) (12)
Анализ различий
Проверка существенности различий заключается в сопоставлении ответов на один и тот же вопрос, полученных для двух или более независимых групп респондентов.
В ряде случаев представляет интерес сравнение ответов на два или более независимых вопроса для одной и той же выборки.
При проведении сравнения различных выборок необходимо принять два критических фактора: степень существенности различий между величинами параметра для двух выборок и средние квадратические ошибки двух выборок, определяемые их объёмами.
Для проверки существенности разницы применяется нулевая гипотеза: предполагается, что две совокупности, сравниваемые по одному или нескольким признакам, не отличаются друг от друга, и различие между сравниваемыми величинами равно нулю, а выявленное по данным отличие от нуля носит случайный характер.
Для проверки существенной разницы между двумя измеренными средними (процентами) вначале проводится их сравнение, затем полученная разница переводится в значение среднеквадратических ошибок и определяется, насколько далеко они отклоняются от гипотетического нулевого значения.
Как только определены среднеквадратические ошибки, становится известной площадь под нормальной кривой распределения и появляется возможность сделать заключение о вероятности выполнения нулевой гипотезы.
Пример: есть ли разница в потреблении прохладительных напитков между юношами и девушками? Юноши потребляют 9 банок в неделю, девушки – 7,5 банок (результат описательной статистики). Средние квадратические отклонения составили 2 (юноши) и 1,2 (девушки). Объём выборки в обоих случаях – 100 человек. Проверка статистической разницы определяется по формуле 13:
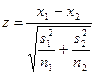 (13),
(13),
где х1 и х2 – средние для двух выборок
s1 и s2 – средние квадратические отклонения для двух выборок
n1 и n2 – объём первой и второй выборок
Имеем:
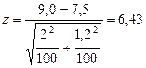
Величина z = 6,43 значительно превышает значение z для 99% уровня доверительности. Следовательно, нулевая гипотеза не является истинной.
Дата добавления: 2017-01-29; просмотров: 2513;
