Анализ связи атрибутивных признаков.
Взаимосвязь между атрибутивными признаками анализируется посредством таблиц взаимной сопряженности.
При наличии статистической связи оценка тесноты связи базируется на отклонениях фактических частот 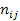 от
от 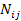 пропорциональным итоговым частотам:
пропорциональным итоговым частотам:
 , (5.38)
, (5.38)
где 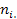 - суммарные частоты по
- суммарные частоты по 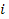 - той строке;
- той строке;
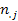 - суммарные частоты по j
- суммарные частоты по j  - тому столбцу;
- тому столбцу;
 - объем совокупности.
- объем совокупности.
Абсолютную величину отклонений фактических частот 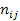 от
от 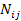 характеризуют критерием
характеризуют критерием 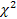 («хи»-квадрат):
(«хи»-квадрат):
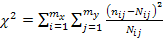 , (5.39)
, (5.39)
где  – соответственно количество групп по признакам
– соответственно количество групп по признакам 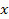 и
и 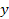 .
.
При отсутствии статистической связи 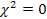 .
.
Для вывода о тесноте связи рассчитанное значение 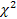 сравнивается с табличным значением
сравнивается с табличным значением 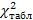 , которое выбирается из таблиц распределения «хи»-квадрат в зависимости от принятого уровня значимости α и степеней свободы
, которое выбирается из таблиц распределения «хи»-квадрат в зависимости от принятого уровня значимости α и степеней свободы 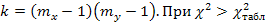 делают вывод о наличии тесной связи между признаками
делают вывод о наличии тесной связи между признаками 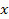 и
и 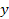 .
.
Относительной мерой тесноты статистической связи между признаками служат:
· коэффициент взаимной сопряженности Чупрова
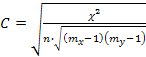 ; (5.40)
; (5.40)
· коэффициент взаимной сопряженности Крамера
V 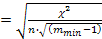 , (5.41)
, (5.41)
где 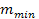 – минимальное количество групп (
– минимальное количество групп ( 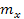 или
или 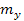 ).
).
Значение коэффициентов изменяется от 0 до 1, и теснота связи тем сильнее, чем ближе к 1.
Пример 5.7.По результатам опроса 48 абитуриентов получены следующие данные о выборе специальности
Необходимо определить: влияет ли пол на выбор специальности?
Для этого воспользуемся критерием «хи»-квадрат. Построим таблицу распределения частот:
Теоретически, мы ожидаем, что частоты распределятся равномерно, т.е. частота распределится пропорционально между юношами и девушками. Построим таблицу теоретических частот. Для этого умножим сумму по строке на сумму по столбцу и разделим получившееся число на общую сумму (n).
Итоговая таблица для вычислений будет выглядеть так:
Из таблицы распределения Т.к. Коэффициент взаимной сопряженности Чупрова (5.40): коэффициент взаимной сопряженности Крамера (5.41): V |
Если необходимо оценить тесноту связи между альтернативными признаками, которые могут принимать любое число вариантов значений, применяется коэффициент взаимной сопряженности Пирсона (КП ).
Коэффициент взаимной сопряженности Пирсона определяется по формуле:
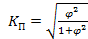 , (5.42)
, (5.42)
где 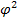 - показатель средней квадратической сопряженности:
- показатель средней квадратической сопряженности:
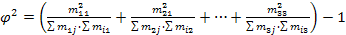 .
.
Коэффициент взаимной сопряженности изменяется от 0 до 1.
Пример 5.8.Оценить тесноту связи между атрибутивными признаками (возрастом и оценкой деятельности политика) при социологическом опросе по данным таблицы:
Коэффициент взаимной сопряженности Пирсона (5.42): Величина |
Наконец, следует упомянуть коэффициент корреляции знаков Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации. Данный коэффициент определяется по формуле:
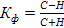 , (5.43)
, (5.43)
где С - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической;
Н - соответственно количество несовпадений.
Коэффициент Фехнера может изменяться в пределах -1,0 ≤ Кф ≤ +1,0.
Дата добавления: 2016-06-02; просмотров: 871;

 48
48
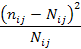
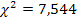 ; число степеней свободы
; число степеней свободы 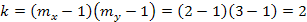 .
.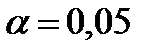 и
и 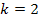 найдем
найдем 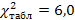 .
.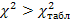 делаем вывод, что пол определяет выбор специальности.
делаем вывод, что пол определяет выбор специальности. ;
; .
.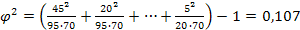
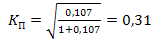 .
.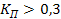 , что свидетельствует о тесноте связи между атрибутивными признаками.
, что свидетельствует о тесноте связи между атрибутивными признаками.