Вычисление доходности на основе сложных процентов (фактической доходности).

В дополнение к купонным платежам и приросту капитала потенциально существует третий источник дохода, который широко не осознан большинством инвесторов. Это доход, который появляется, когда вместо расходования ежегодных процентных платежей владелец облигации реинвестирует эти купонные выплаты по мере того, как они поступают. Действительно, как ни удивительно это может показаться, держатели облигации никогда не получат обещанной доходности на свои инвестиции в ценные бумаги с фиксированным доходом, если они не реинвестируют купонные выплаты под ставку процента, равную первоначальной доходности к погашению. Такое вычисление доходности облигаций подобно начислению сложных процентов, показанное в главе 9 и проиллюстрированное на рис.9.1. Приведенный там пример начисления сложных процентов показывает, что совокупный денежный доход, который извлек бы инвестор в результате покупки облигации, зависит в большей части от процентов, которые могут быть получены в результате реинвестирования купонов.

Оценка фактической доходности к погашению облигации может быть выполнена при помощи калькулятора, аналогично вычислению по методу сложных процентов. К тому же такая оценка может быть осуществлена на основе таблицы доходности по облигациям (фрагмент таблиц доходности см. табл.12.1).

Таблица12.1.

Фрагмент таблицы доходности облигации

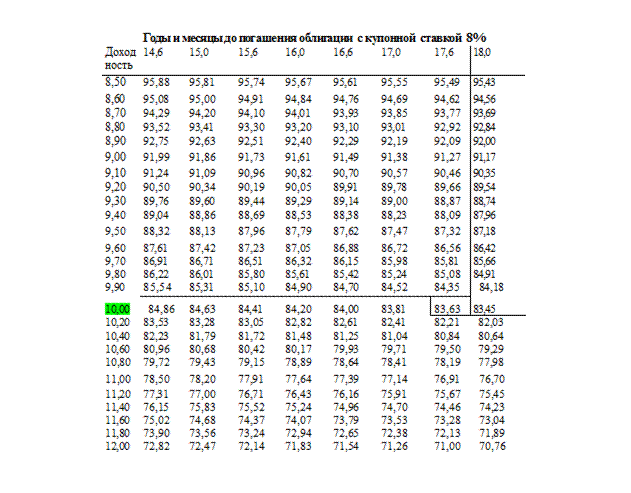
Пользоваться таблицей довольно просто. Допустим, что Вы хотите найти доходность облигации с 8%-м купоном, которая в настоящее время продается с дисконтом по курсу 83,63 (это означает цену 836,3 долл.) и до ее срока погашения остается 17 лет и 6 месяцев. Для нахождения доходности нужно посмотреть ту страницу книги доходности облигаций, где отражены данные 8%-х купонных облигаций (см. табл.12.1). Далее найти число лет и месяцев до момента погашения в верхней части страницы (17,6). Затем пробежать по колонке до значения курса облигации (83,63) и в крайней левой колонке прочесть значение доходности к погашению (10%).

Основное допущение стандартных вычислений доходности к погашению в том, что предполагается постоянное реинвестирование всех купонов по ставке, равной доходности к погашению этой облигации. Когда такое допущение неправомерно из-за текущих потребительских расходов либо из-за изменений в рыночных процентных ставках, вычисление доходности к погашению не дает полной рассчитанной на основе сложных процентов доходности инвестиций в облигации. Вычисление доходности на основе сложных процентов обходит допущение о ставке реинвестирования, равной доходности к погашению. Это достигается путем внедрения в расчеты, любой ставки реинвестирования, которая может, конечно, отличаться от первоначальной доходности к погашению облигации возникшей на момент ее приобретения.

Таким образом, опытный инвестор, осуществляющий операции с облигациями, учитывает изменяющиеся рыночные ставки реинвестирования, предполагает ставку доходности, на которую можно рассчитывать, реинвестируя полученные купоны. Такая ставка процента известна как ставка реинвестирования, а вычисление доходности облигации, в которой специально учитываются эти изменения в рыночных процентных ставках, приводит к результату, известному как полная доходность к погашению, вычисленная на основе сложных процентом, или эффективная ставка доходности.

Полная доходность к погашению данной облигации с применением сложного процента может быть подсчитана по следующей формуле:

Фактор дисконтирования потоков денежных средств по облигации =

= Курс покупки облигации / (Купон * Фактор наращения аннуитета +

+ Номинальная стоимость облигации),

где курс покупки облигации – это цена, которую инвестор должен заплатить за облигацию;

купон – стоимость ежегодных купонных выплат;

фактор наращения аннуитета – фактор будущей стоимости аннуитета из приложения Б1,Б2 для числа периодов, равного сроку до погашения, и предлагаемой ставки реинвестирования купона;

номинальная стоимость облигации – стоимость, которая должна быть получена при ее погашении (обычно 1000 долл.).

Фактор дисконтирования, вычисленный здесь, используется затем в работе с таблицей приведенной стоимости вместе с параметром числа лет до погашения облигации, чтобы получить эффективную, т. е. вычисленную на основе сложных процентов, доходность к погашению (полную доходность к погашению, фактическую доходность).

Хотя ставка реинвестирования – решающая переменная в вычислении полной доходности к погашению на базе сложных процентов в случае облигаций с длительным сроком погашения, ее воздействие на краткосрочные облигации незначительно.