Разнообразие инвестиционных стратегий

Профессиональные финансовые менеджеры, а также индивидуальные инвесторы используют различные методы для размещения имеющихся в их распоряжении портфелей облигаций. В число стратегий профессионалов входят пассивные, полуактивные, а также активные, полностью управляемые стратегии, использующие прогнозирование процентных ставок и анализ спрэда доходности облигаций. В большинстве своем эти стратегии являются довольно сложными, требующими значительного компьютерного обеспечения, и, кроме того, они требуют достаточно больших инвестиционных ресурсов.

Частный инвестор имеет совсем иные потребности и ресурсы по сравнению с крупными институциональными инвесторами. Как правило, среди частных инвесторов популярны следующие инвестиционные стратегии формирования портфелей облигаций (разумеется, они также используются институциональными инвесторами, но на более сложной, аналитической основе): стратегия длительного владения облигациями, стратегия систематической торговли облигациями, основанная на прогнозируемом изменении процентных ставок, и стратегия свопов с облигациями.

Пассивная инвестиционная стратегия априори полагает, что рыночные курсы ценных бумаг установлены справедливо, поэтому нет нужды анализировать и выявлять «недооцененные» или «переоцененные» ценные бумаги, а также и нет необходимости в прогнозировании изменения процентных ставок, влияющих на изменение курса облигаций.

Особый случай пассивной стратегии – иммунизация портфеля, которая пытается оградить портфель от риска колебания процентных ставок. Существует разновидность иммунизации, так называемая стратегия ограниченной иммунизации, которую можно назвать полуактивной.

Активная инвестиционная стратегия пытается обеспечить доходность, не просто соизмеримую с риском, но и обеспечивающую сверхдоходность. Этот стиль управления облигациями может принимать две формы:

1) прогнозирование процентных ставок, с целью предвидения изменения всего рынка ценных бумаг с фиксированных доходом;

2) внутрирыночный анализ различных секторов рынка облигаций, с целью выявления ценных бумаг «неправильно» оцененных рынком.

Дюрация

Прежде, чем приступить к характеристике конкретных стратегий, необходимо раскрыть сущность понятия «дюрация». Это важно, поскольку, как известно, процентные ставки являются решающим фактором, воздействующим на цену облигации, а дюрация измеряет чувствительность цен облигаций к изменениям процентных ставок.

Финансовые аналитики выявили следующие соотношения между ценой облигации и колебаниями процентных ставок:

1. Цены и доходность облигаций связаны между собой обратно пропорциональной зависимостью: когда доходность повышается, цены облигаций снижаются; когда доходность падает, цены облигаций повышаются.

2. Повышение доходности облигации приводит к меньшему снижению цены, чем приращение цены, связанное с таким же (по абсолютной величине) уменьшением доходности.

3. Цены долгосрочных облигаций, как правило, более чувствительны к изменениям процентных ставок, чем цены краткосрочных облигаций.

4. Чувствительность цен облигаций к изменениям доходности повышается снижающимися темпами при увеличении сроков погашения облигаций. Иными словами, процентный риск облигаций не прямо пропорционален увеличению сроков погашения облигаций – он изменяется в несколько меньшей степени.

5. Процентный риск связан с купонной ставкой облигации обратно пропорциональной зависимостью. Цены облигаций с высокими купонными ставками менее чувствительны к изменениям процентных ставок, чем цены облигаций с низкими купонными ставками.

6. Цены облигаций более чувствительны к изменениям доходности, когда облигация продается с пониженной начальной доходностью при погашении.

Устойчивость, дюрация или длительность облигации (duration) – мера действительного, в противоположность номинальному, эффективного срока погашения ценной бумаги с фиксированным доходом. Только облигации, обещающие единственную выплату, которая происходит в момент погашения (т. е. купоны не оплачиваются ежегодно), обладают длительностью, равной их номинальному числу лет до срока погашения. Облигации с нулевым купоном — именно такие облигации. Для всех других срок действия всегда короче, чем их номинальный срок до погашения.

В то время как срок до погашения облигации (номинальный) – несомненно, полезное понятие, ему не удается быть хорошим измерителем действительной жизни облигации, поскольку он не принимает в расчет все потоки денежных средств по облигации или стоимость денег во времени. Скорее срок до погашения облигации имеет отношение только к определению времени ее конечного платежа при погашении.

Устойчивость облигации — гораздо более удачная характеристика действительного графика движения денежного потока по облигации во времени, поскольку она учитывает, с одной стороны, стоимость денег во времени и ее купонные платежи, и основную сумму погашения – с другой. Макоули предложил термин «дюрация» и способ ее вычисления. Устойчивость, дюрацию или длительность облигации можно определить как средневзвешенный срок до погашения облигации, где весовой фактор для каждого потока денежных средств по облигации – это удельный вес приведенной стоимости потоков денежных средств относительно рыночного курса облигации. Математически это выглядит следующим образом:

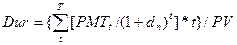, (12.10)

где Dur – дюрация, устойчивость;

РМТ_t - выплата процентов и (или) суммы погашения в момент t ;

d_n – доходность к погашению облигации;

T – нормативный срок погашения облигации.

При прочих равных условиях, чем больше купонные платежи облигации, тем короче ее средневзвешенный срок. Это так, поскольку фактор дисконтирования облигации для более ранних потоков денежных средств намного выше, чем в последние годы. Аналогично, чем выше доходность облигации к погашению, тем короче ее средневзвешенный срок. Это верно, поскольку более высокие ставки доходности (используемые как ставки дисконтирования в расчете) уменьшают приведенную стоимость денежных потоков, которые должны быть получены в отдаленном будущем.

На рисунок 12.3 графически изображен подход Макоули к вычислению дюрации.

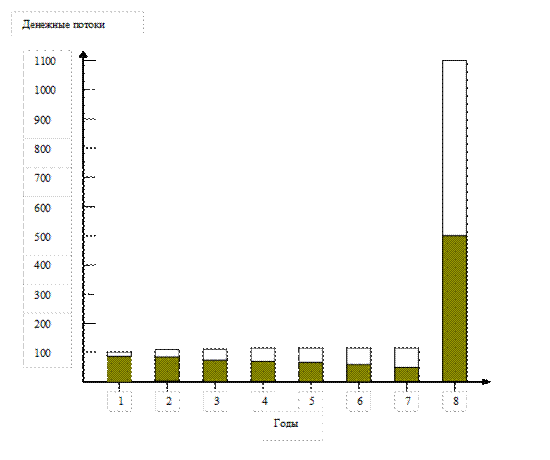
Рис.12.3. Денежные поступления от облигации с 10%-м купоном и 8-летним сроком погашения.

«Светлые» столбики представляют собой номинальные ежегодные выплаты купонных платежей в течение восьми лет срока жизни облигации и суммы основного долга, выплаченного через восемь лет. «Темные» – показывают приведенную стоимость платежа при ставке дисконтирования 10% (ставка дисконтирования равна доходности к погашению данной облигации).

Если представить, что временная шкала некое подобие детских качелей в виде доски с упором посередине, то дюрация облигации это точка упора, при которой суммы приведенных стоимостей по обе стороны от упора равны, и «качели» находятся в равновесии.

В таблице 12.2 показан расчет дюрации для проиллюстрированной на графике облигации.

Таблица 12.2

Пример расчета дюрации облигации с 10%-м купоном, 8-летним сроком погашения и 10%-ой доходностью к погашению

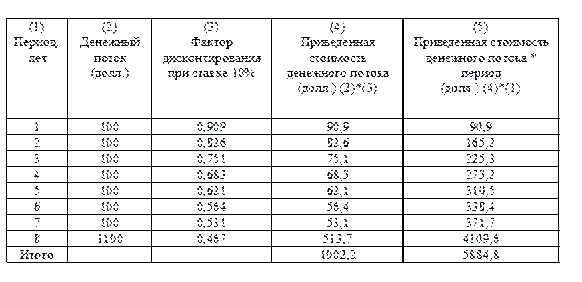
Из таблицы можно вычислить дюрацию: Dur = 5884,8 / 1002,2 = 5,87.

Устойчивость, или длительность, – понятие, относящееся не только к отдельной ценной бумаге. Устойчивость целого портфеля также просто вычисляется. Все, что требуется, – это средневзвешенные сроки отдельных ценных бумаг портфеля и пропорции, в которых каждая ценная бумага делает вклад в общую стоимость портфеля. В итоге устойчивость портфеля равна средневзвешенной величине устойчивости каждой ценной бумаги в портфеле, где вес – доля каждой отдельной ценной бумаги в рыночной стоимости всего портфеля.

Изменчивость курса облигаций является отчасти функцией от срока их погашения, а отчасти от купонной ставки. К сожалению, не существует строгого соотношения между сроками погашения облигаций и изменчивостью их курса относительно сдвигов в уровнях процентных ставок. Существует, однако, почти точное соотношение между показателем устойчивости облигаций и изменчивостью их курсов. Если умножить значение устойчивости облигации на -1, то получим ее ценовую эластичность по рыночной процентной ставке. Таким образом, вычисляя устойчивость облигации, можно получить точный измеритель того, насколько ее курс будет изменяться по отношению к данному изменению рыночной ставки процента. Математическая зависимость между курсом облигации и изменением процентных ставок выражается понятием модифицированной устойчивости (модифицированная дюрация) (modified duration). Соответствующая формула выглядит следующим образом (для компаундирования – вычисление сложного процента –один раз в год):

Модифицированная устойчивость(MDur) = Дюрация / (1 + Доходность к погашению),

или:

MDu r= Dur / (1+d/m);

если компаундирование осуществляется m раз в год.

Таким образом, величину модифицированной устойчивости для облигации со сроком погашения через 8 лет, рассмотренной выше, можно определить следующим образом:

Модифицированная устойчивость = 5,87 / (1+0,10) = 5,34.

Для определения относительных отклонений курса этой облигации в процентах в результате изменения рыночных ставок процента с 12 до 12,5 значение модифицированной устойчивости, подсчитанной выше, сначала умножается на -1 (из-за обратной зависимости между курсами облигаций и рыночными ставками процента) и затем на изменение уровня рыночной процентной ставки:

Относительное изменение курса облигации (в %) = (-1) * Модифицированная устойчивость * Изменение процентной ставки = (-1) * 5,34 * 0,5% = -2,67%.

Таким образом, изменение рыночной процентной ставки на 0,5 приведет почти к 2,67%-му падению курса облигации с купонной ставкой 10% и сроком до погашения 8 лет. Такая информация полезна инвесторам, вкладывающим средства в облигации, которые ищут (или стремятся избежать) высокий ценовой риск.