Теориялық механиканың негізгі ұғымдары 4 страница
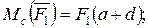
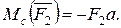
Осы теңдіктердің оң және сол жазықтығы мүшелерін өзара қосайық
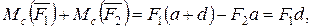
немесе
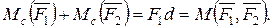
Қос күштің бұл қасиетінен мынаны тұжырымдауға болады: кез келген момент центрлеріне қатысты құрылған момент теңдеулеріне қос күш бірдей таңбамен және бірдей шамамен кіреді, яғни қос күш моментінің таңбасы мен шамасы момент центрінен тәуелсіз.
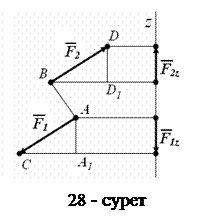 Үшінші қасиеті. Қос күштің құраушы күштерінің өске проекцияларының алгебралық қосындысы әрқашан нөлге тең.
Үшінші қасиеті. Қос күштің құраушы күштерінің өске проекцияларының алгебралық қосындысы әрқашан нөлге тең.
 қос күші және қос күштің әсер жазықтығында жататын
қос күші және қос күштің әсер жазықтығында жататын  өсі берілсін делік (28 - сурет).
өсі берілсін делік (28 - сурет).
Суретте көрсетілген  және
және 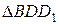 үшбұрыштарының теңдігінен
үшбұрыштарының теңдігінен 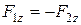 екені аңғарылады.
екені аңғарылады.
Бұл проекциялардың алгебралық қосындысы әрқашан нөлге тең, өйткені 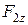 проекциясы оң таңбалы да
проекциясы оң таңбалы да 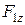 проекциясы теріс таңбалы.
проекциясы теріс таңбалы.
Атап өтсек, қос күш не күш теңдеулеріне, не күштің проекциялық теңдеулеріне кірмейді.
3-лекция (2-ші лекция жалғасы)
Қос күштер эквиваленттілігі. Еркін қатты дененің механикалық күйін өзгертпей бір қос күшті екінші бір қос күшпен алмастыруға мүмкін болса, онда бұл қос күштер пара-пар немесе эквивалентті деп аталады.
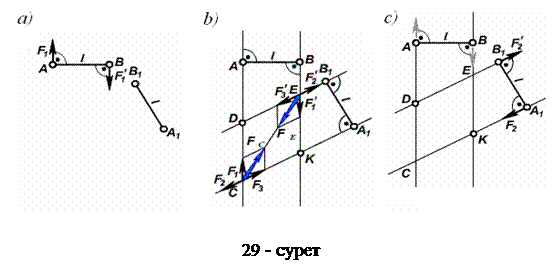
1 теорема. Қос күштің денеге әсер, оны әсер ету жазықтығында басқа орынға ауыстырғаннан өзгермейді.
Иіні 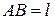
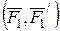 қос күші беріліп, қос күшті иіні
қос күші беріліп, қос күшті иіні 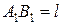 болатын кездейсоқ алынған орынға ауыстыру қажет болсын делік (29, а – сурет).
болатын кездейсоқ алынған орынға ауыстыру қажет болсын делік (29, а – сурет).
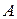 мен
мен 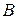 және
және 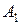 мен
мен 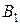 нүктелерінен, сәйкесінше
нүктелерінен, сәйкесінше 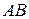 және
және 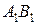 кесінділеріне перпендикуляр, параллель түзулер жүргізейік (29, b – сурет). Екі параллель түзудің екінші параллель түзумен қиылысады және қиылысында
кесінділеріне перпендикуляр, параллель түзулер жүргізейік (29, b – сурет). Екі параллель түзудің екінші параллель түзумен қиылысады және қиылысында 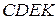 ромб пайда болады (өйткені берілгені бойынша
ромб пайда болады (өйткені берілгені бойынша 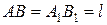 , ал параллелограмның бір төбесінен түсірілген биіктіктер тең болса, онда ол ромб).
, ал параллелограмның бір төбесінен түсірілген биіктіктер тең болса, онда ол ромб). 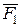 күшін әсер ету сызығының бойымен
күшін әсер ету сызығының бойымен 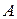 нүктесінен
нүктесінен 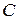 нүктесіне, ал
нүктесіне, ал 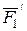 күшін
күшін 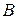 нүктесінен
нүктесінен 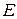 нүктесіне түсірейік.
нүктесіне түсірейік. 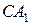 түзуінің бойымен
түзуінің бойымен 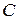 нүктесіне, модульдері
нүктесіне, модульдері 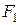 -ге тең теңестірілген
-ге тең теңестірілген 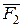 және
және 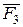 күштер жиынын түсірейік;
күштер жиынын түсірейік; 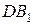 түзуінің бойымен
түзуінің бойымен 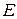 нүктесіне де модульдері
нүктесіне де модульдері 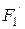 -ке тең, теңестірілген
-ке тең, теңестірілген 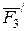 және
және 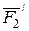 күштер жүйесін түсірейік, сонымен
күштер жүйесін түсірейік, сонымен 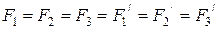 .
.
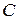 нүктесіне түсірілген
нүктесіне түсірілген 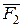 және
және  күштерінің тең әсерлі
күштерінің тең әсерлі 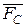 күшін және
күшін және 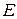 нүктесіне түсірілген
нүктесіне түсірілген 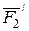 және
және 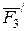 күштерінің тең әсерлі
күштерінің тең әсерлі 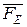 күшін анықтайық.
күшін анықтайық. 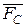 пен
пен 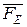 күштері бірін-бірі теңестіретінін аңғару қиын емес, өйткені олардың шамалары өзара тең және олар
күштері бірін-бірі теңестіретінін аңғару қиын емес, өйткені олардың шамалары өзара тең және олар 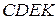 ромбасының диагоналының бойымен қарама-қарсы бағытта әсер етеді. Сонымен,
ромбасының диагоналының бойымен қарама-қарсы бағытта әсер етеді. Сонымен, 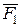 ,
, 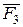 ,
, 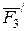 және
және 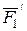 күштері теңестірілген күштер жиынын құрайды, яғни
күштері теңестірілген күштер жиынын құрайды, яғни 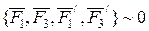 . Олай болса оларды қарастырмай-ақ қойуға болады, сонда қарастырылған күштер жиынынан тек екі күш қалады,
. Олай болса оларды қарастырмай-ақ қойуға болады, сонда қарастырылған күштер жиынынан тек екі күш қалады, 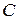 нүктесіндегі
нүктесіндегі 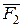 күші мен
күші мен 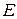 нүктесіндегі
нүктесіндегі 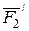 күші. Бұл күштерді әсер сызықтарының бойымен жылжыта отырып, сәйкесінше
күші. Бұл күштерді әсер сызықтарының бойымен жылжыта отырып, сәйкесінше 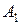 және
және 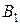 нүктелеріне түсірсек, онда иіні
нүктелеріне түсірсек, онда иіні 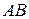 болатын
болатын 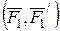 қос күшіне пара-пар келетін иіні
қос күшіне пара-пар келетін иіні 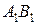 -ге тең
-ге тең 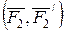 қос күшін аламыз (29, c – сурет), өйткені күштердің
қос күшін аламыз (29, c – сурет), өйткені күштердің 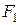 ,
, 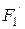 ,
, 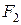 және
және 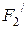 модульдері және
модульдері және 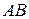 мен
мен  иіндері тең. Сонымен, берілген қос күшті басқа орынға ауыстырдық (29, c – сурет). Бұл теореманың дәлелденгенін көрсетеді.
иіндері тең. Сонымен, берілген қос күшті басқа орынға ауыстырдық (29, c – сурет). Бұл теореманың дәлелденгенін көрсетеді.
2 теорема. Бір жазықтықта жатқан, моменттері тең екі қос күштің денеге әсерлері өзгермейді.
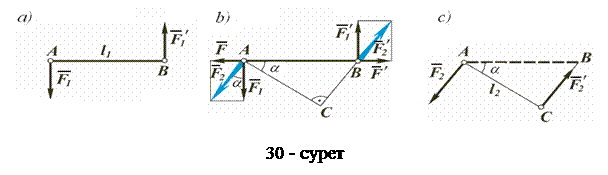 Иіні
Иіні 
 қос күші берілсін делік. Онда, қос моменті
қос күші берілсін делік. Онда, қос моменті 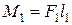 болады (30, а – сурет). Қос күшке
болады (30, а – сурет). Қос күшке 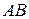 иіні бойымен әсер ететін теңестірілген
иіні бойымен әсер ететін теңестірілген 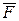 пен
пен 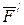 күштерін біріктірейік (30, b – сурет) және
күштерін біріктірейік (30, b – сурет) және 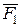 мен
мен 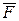 , сонымен қатар
, сонымен қатар 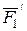 пен
пен 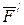 күштерін қос-қостап қосайық. Олардың тең әсерлі күштері
күштерін қос-қостап қосайық. Олардың тең әсерлі күштері 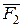 мен
мен 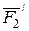 , иіні
, иіні 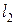 тең жаңа қос күшті құрайды (30, c – сурет). Жоғарыда жүргізілген түрлендірулер статиканың аксиомаларына негізделіп жүргізілді және дененің алғашқы күйін еш өзгертпейді, яғни
тең жаңа қос күшті құрайды (30, c – сурет). Жоғарыда жүргізілген түрлендірулер статиканың аксиомаларына негізделіп жүргізілді және дененің алғашқы күйін еш өзгертпейді, яғни 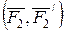 қос күші денеге
қос күші денеге 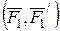 қос күшіндей әсер етеді. Енді қос күштердің моменттерінің теңдігін дәлелдеу керек:
қос күшіндей әсер етеді. Енді қос күштердің моменттерінің теңдігін дәлелдеу керек:
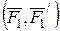 қос күшін,ің моменті
қос күшін,ің моменті 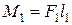 ,
,
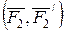 қос күшін,ің моменті
қос күшін,ің моменті 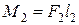 .
.
30, c – суреттегі сызбадан 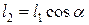 ,
, 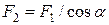 екені көрінеді, олай болса,
екені көрінеді, олай болса, 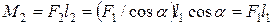 , яғни
, яғни 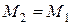 .
.
Теорема дәлелденді.
Бір жазықтықта жататын, әсер ететін моменттері тең қос күштер статикалық тепе-тең деп аталады.
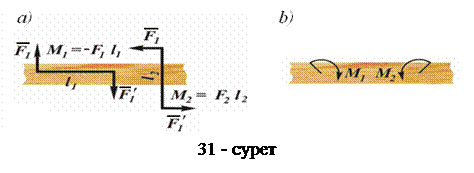 Дәлелденген теорема бойынша берілген жазықтықта жатқан қос күштің айналдыру әсері оның моментіне тәуелді, сондықтан қос күштің берілуін оның моментінің шамасын көрсетсе жеткілікті, онан кейін берілген немесе таңдап алынған иін бойынша қосақтағы күштің мәнін немесе күш бойынша қажетті иінді анықтауға болады. Осыған байланысты суреттер мен сызбаларда қос күшті оның айналдыру әсерінің бағытын көрсететін дөңгелек жебемен кескіндейді. Мысалы, білеуге түсірілген қос күшті (31, а – сурет), оларды
Дәлелденген теорема бойынша берілген жазықтықта жатқан қос күштің айналдыру әсері оның моментіне тәуелді, сондықтан қос күштің берілуін оның моментінің шамасын көрсетсе жеткілікті, онан кейін берілген немесе таңдап алынған иін бойынша қосақтағы күштің мәнін немесе күш бойынша қажетті иінді анықтауға болады. Осыған байланысты суреттер мен сызбаларда қос күшті оның айналдыру әсерінің бағытын көрсететін дөңгелек жебемен кескіндейді. Мысалы, білеуге түсірілген қос күшті (31, а – сурет), оларды  және
және  деп белгіленген дөңгелек жебемен шартты түрде кескіндеуге болады (31, b – сурет).
деп белгіленген дөңгелек жебемен шартты түрде кескіндеуге болады (31, b – сурет).
Қос күштерді қосу. Қос күштердің тепе-теңдік шарты. Теорема. Денеге бір жазықтықта әсер ететін қос күштер жиыны, моменті қос күштердің моменттерінің алгебралық қосындысына тең болатын қос күшпен тепе-тең.
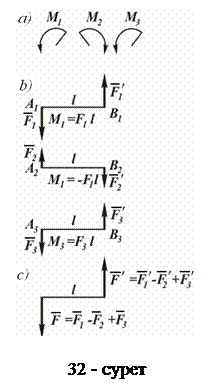 Бір жазықтықта жататын моменттері
Бір жазықтықта жататын моменттері  ,
,  және
және  болатын үш қос күш берілсін делік (32, а – сурет). Берілген қос күштерді оларға тепе-тең иіндері бірдей
болатын үш қос күш берілсін делік (32, а – сурет). Берілген қос күштерді оларға тепе-тең иіндері бірдей 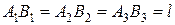
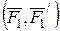 ,
, 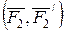 және
және 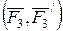 қос күштерімен алмастырайық, яғни
қос күштерімен алмастырайық, яғни 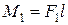 ,
, 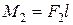 және
және 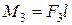 және осы қос күштерді, олардың күштері екі параллель түзудің бойымен әсер ететіндей етіп орналастырайық (32, b – сурет).
және осы қос күштерді, олардың күштері екі параллель түзудің бойымен әсер ететіндей етіп орналастырайық (32, b – сурет).
Бір түзудің бойында әсер ететін күштердің тең әсерлі күші, осы түздің бойымен бағытталатыны және модулі құраушы күштердің шамаларының алгебралық қосындысына тең екені бізге белгілі. Олай болса, 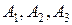 нүктелері мен
нүктелері мен 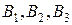 нүктелеріне түсірілген күштерді қосып, берілген үш қос күштеріне тепе-тең
нүктелеріне түсірілген күштерді қосып, берілген үш қос күштеріне тепе-тең 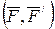 қос күшін, аламыз (32, c – сурет). Сонымен қатар
қос күшін, аламыз (32, c – сурет). Сонымен қатар 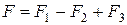 .
.
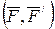 тең әсерлі қос күшінің моменті
тең әсерлі қос күшінің моменті 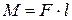 , ал
, ал 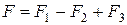 болғандықтан
болғандықтан
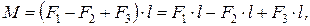
немесе
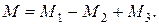 (27)
(27)
Теорема дәлелденді.
(27) теңдігінің жалпылама түрі былайша жазылады
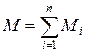 . (28)
. (28)
Сонымен, денеге бір жазықта әсер ететін бірнеше қос күштерді қосу үшін, осы қос күштерінің моменттерінің алгебралық қосындысын анықтаса жеткілікті. Қосу нәтижесінде алынған момент тең әсерлі қос күшті анықтайды.
Егер қосу нәтижесінде 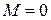 болса, онда денеге әсер ететін қос күштер теңестірілген қос күштерді құрайды. Сонымен, қос күштер жиынының тепе-теңдігінің қажетті және жеткілікті шарты бір теңдеумен өрнектеледі
болса, онда денеге әсер ететін қос күштер теңестірілген қос күштерді құрайды. Сонымен, қос күштер жиынының тепе-теңдігінің қажетті және жеткілікті шарты бір теңдеумен өрнектеледі
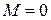 , (29)
, (29)
яғни денеге бір жазықта әсер етуші қос күштер жиыныі тепе-теңдікте болу үшін жиындағы қос күштер моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті.
Сонымен, қос күштер жиынын немесе бір қос күшті тек қос күшпен теңестіруге болады.
Еркін орналасқан жазық күштердің жиыны. Күшті берілген нүктеге келтіру. Екі ғасырдай бұрын Л. Пуансо күшті кез келген берілген немесе таңдап алынған нүктеге көшіруге болатыны жөніндегі теореманы дәлелдеді.
Денеге әсер ететін кез келген 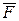 күшін дененің қандай да бір
күшін дененің қандай да бір 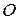 нүктесіне өзіне-өзі параллель көшіруге қажет делік (33, а – сурет). Ол үшін,
нүктесіне өзіне-өзі параллель көшіруге қажет делік (33, а – сурет). Ол үшін, 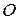 келтіру нүктесіне
келтіру нүктесіне 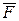 күшіне параллель теңестірілген
күшіне параллель теңестірілген 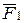 ,
, 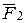 күш жүйесін түсірейік (33, b – сурет), яғни
күш жүйесін түсірейік (33, b – сурет), яғни 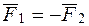 ,
, 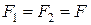 ,
, 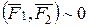 ,
, 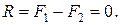 Енді
Енді 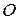 нүктесінде түсірілген
нүктесінде түсірілген 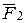 күшімен қатар, моменті
күшімен қатар, моменті 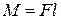 қос күш
қос күш 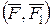 пайда болды (33, c – сурет). Бір жағынан берілген
пайда болды (33, c – сурет). Бір жағынан берілген 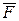 күштің
күштің 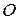 келтіру нүктесіне қарағандағы моменті де
келтіру нүктесіне қарағандағы моменті де 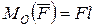 , яғни
, яғни 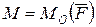 .
.
Сонымен, денеге әсер ететін кез келген күшті дененің қандай да бір нүктесіне өзіне-өзі параллель көшіруге болады, бұл жағдайда келтіру нүктесіне күшпен қатар моменті берілген күштің жаңа түсіру нүктесіне  қатысты моментіне тең қос күшті қосу қажет.
қатысты моментіне тең қос күшті қосу қажет.
Осы сияқты күштің орнын ауыстыруды күшті берілген нүктеге келтіру деп атайды, ал туындаған моменті 
 қос күшін тіркеме қос күш дейді.
қос күшін тіркеме қос күш дейді.
Еркін орналасқан жазық күштер жиынын берілген нүктеге келтіру. 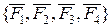 жазық күштер жиыны берілген делік және оның құраушы күштері бір-біріне параллель емес және олардың әсер ету сызықтары бір нүктеде қиылыспайды (34 – сурет).
жазық күштер жиыны берілген делік және оның құраушы күштері бір-біріне параллель емес және олардың әсер ету сызықтары бір нүктеде қиылыспайды (34 – сурет).
 Кез келген
Кез келген  нүктесін келтіру нүктесі деп алып, оған алдымен
нүктесін келтіру нүктесі деп алып, оған алдымен  күшін келтірейік, яғни
күшін келтірейік, яғни 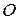 нүктесіне
нүктесіне 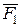 күшін ауыстырып,
күшін ауыстырып, 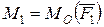 мо-ментін тіркейік. Одан кейін
мо-ментін тіркейік. Одан кейін 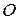 нүктесіне
нүктесіне 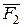 күшін ауыстырып, оның
күшін ауыстырып, оның 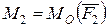 моментін тіркейік. Басқа
моментін тіркейік. Басқа 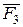 ,
, 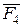 күштерімен де осындай әрекет жасап, келтіру
күштерімен де осындай әрекет жасап, келтіру 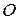 нүктесін
нүктесін 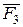 ,
, 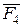 күштерімен қатар олардың сәйкес
күштерімен қатар олардың сәйкес 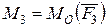 және
және 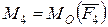 моменттерін түсірейік. 34 – суретінен көрінетіндей, келтіру нүктесінде жинақталған күштер жиыны мен моменті берілген күштердің моментіне тең тіркеме қос күштер жиыны пайда болды.
моменттерін түсірейік. 34 – суретінен көрінетіндей, келтіру нүктесінде жинақталған күштер жиыны мен моменті берілген күштердің моментіне тең тіркеме қос күштер жиыны пайда болды.
Жинақталған күштер жиынының векторлық қосындысын анықтап, келтірілген күштердің тепе-теңдік күшін аламыз
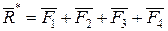 .
.
Сонымен, берілген күштер жиынының векторлық қосындысына тең 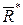 күшін күштер жиынының бас векторы деп атайды және ол келтіру нүктесіне түсіріледі. Тіркеме қос күштердің моменттерінің алгебралық қосындысын есептеп, олардың тепе-теңдік қос күшінің моментін анықтаймыз
күшін күштер жиынының бас векторы деп атайды және ол келтіру нүктесіне түсіріледі. Тіркеме қос күштердің моменттерінің алгебралық қосындысын есептеп, олардың тепе-теңдік қос күшінің моментін анықтаймыз
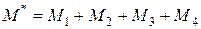
немесе
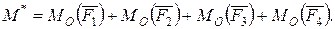
Берілген күштердің келтіру нүктесіне қарағандағы моменттерінің алгебралық қосындысы бас момент деп аталады.
Бас вектор мен бас моменттің, жалпы жағдайда жазылу түрі
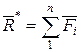 , (30)
, (30)
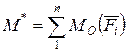 . (31)
. (31)
Бас күш графикалық жағынан берілген күштерден тұрғызылған көпбұрыштың тұйықтаушы қабырғасы болып табылады. Бас вектордың модулін аналитикалық жолмен мына формуланы пайдаланып есептеуге болады
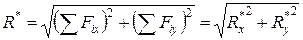 , (32)
, (32)
мұнда 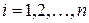 .
.
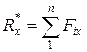 ,
, 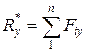 . (33)
. (33)
Бас күштің бағыттаушы косинустары
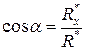 ,
, 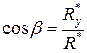 . (34)
. (34)
Бас вектор берілген жазық күштер жиынының теңестіруші күші емес, өйткені ол берілген жүйені тек тіркеме бас моментпен бірге алмастыра алады.
Қасиеттері. 1 Берілген күштер жиынының бас векторының модулі мен бағыты келтіру нүктесінің орнына тәуелсіз.
2 Жалпы жағдайда бас моменттің шамасы мен таңбасы келтіру нүктесінің орнына тәуелді.
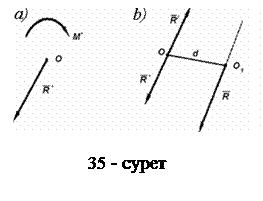
Жазық күштер жиынының тең әсерлі күші. Вариньон теоремасы. Қандай да бір еркін бағытталған 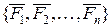 жазық күштер жиынының бас векторы
жазық күштер жиынының бас векторы 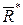 мен бас моменті
мен бас моменті 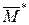 берілген делік (35, а – сурет). Осы жиынның
берілген делік (35, а – сурет). Осы жиынның  тең әсерлі күшін анықтайық.
тең әсерлі күшін анықтайық.
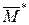 бас моментті
бас моментті 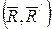 қос күшімен алмастырайық, мұнда
қос күшімен алмастырайық, мұнда 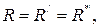
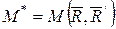 . Қос күштің иіні
. Қос күштің иіні 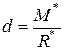 (35, b – сурет).
(35, b – сурет).
Ал 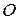 нүктесіндегі
нүктесіндегі 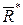 пен
пен 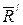 күштері теңестірілген күштер, яғни
күштері теңестірілген күштер, яғни 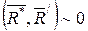 , олай болса, келтіру нүктесінен
, олай болса, келтіру нүктесінен 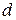 аралықтағы нүктеге түсірілген
аралықтағы нүктеге түсірілген 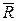 - тең әсерлі күші ғана қалады.
- тең әсерлі күші ғана қалады. 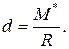
Дата добавления: 2017-01-13; просмотров: 2877;
