Материалдар кедергісінің негізгі ұғымдары
Материалдар кедергісінің міндеттері. Тұрмыстағы кез келген машиналар мен инженерлік құрылыстарды көбірек немесе кемірек күрделі материалдық құрылым ретінде қарастыруымызға болады. Олар жеке элементтерінің алғашқы пішіні мен өлшемдерін сақтай отырып, берілген кейбір жағдайларда әлдеқайда үлкен әсер ететін жүктерге қарсылық көрсетуі тиіс. Мысалы: көпірдің тіректеріне оның салмағы мен үстінен өтіп бара жатқан көліктің салмағы беріледі; автомобильдің иін тірегіне газдың қысымы түседі, ұшақтың қанаттарына аэродинамикалық күштер әсер етеді, т.т. Теориялық механикада тірек реакцияларын анықтағанда, есепте қарастырылатын конструкция элементтерінің пішіні мен өлшемдерінің сақталуы туралы мәселелер туындаған жоқ, өйткені олар абсолют қатты - өзгермейтін дене деп қарастырылды. Іс жүзінде, барлық қатты материалды денелер сыртқы күш әсерінен деформацияланады, яғни олардың пішіні мен өлшемдері өзгереді.
Сонымен, қандай да болмасын механизмдер мен машиналарды жасағанда, құрылыс конструкцияларын тұрғызғанда және т.б. дайындағанда, олардың бөлшектері, бүтін машина, тұрғызылған ғимараттар жеткілікті берік, қатаң, орнықты болуы тиіс, яғни оларға әсер ететін сыртқы күштерге қирамай, алғашқы пішіндері мен өлшемдерін өзгертпей төтеп беруі тиіс.
Бір қарағанда, осы талаптарға оп-оңай жетуге болатын секілді, яғни жасалатын машина бөлшектері мен конструкция элементтерінің өлшемдерін үлкейтсек, қажетті беріктік пен қатаңдық қамтамасыз етілетіндей. Бұл жағдайда машина мен конструкциялардың өлшемдері де үлкейеді, салмағы да ауырлайды, дайындауға көп материал жұмсалады, нәтижесінде құрылымның бағасы қымбаттайды. Сонымен сенімділік пен үнемділіктің бір-біріне қайшылығы туындайды.
«Материалдар кедергісі» ғылымының негізгі мақсаты осы қайшылықтарды шешу болып табылады. «Материалдар кедергісі» курсында әр түрлі материалдардың сыртқы күш әсер еткендегі күйі сипатталады және осы зерттеулерге байланысты әсер етуші күштер мен материалда туындайтын құбылыстар арасындағы тәуелділікті анықтаудың ғылыми әдісі орнатылады. Ал теориялық механикада сыртқы күш әсерінен материалда туындайтын өзгерістер мүлдем қарастырылмайды.
«Материалдар кедергісі» машина мен ғимараттардың әрбір элементтеріне үнемді және сенімді жұмыс істеуіне кепілдік бере отырып, лайықты материалды таңдауға және олардың көлденең өлшемдерін анықтауға көмектеседі, ал сонымен қатар кері есепті де шешеді – тұрғызылған немесе жобаланған конструкция өлшемдерінің жеткіліктігін тексеру, яғни бұл пәннің міндеті салмағы жағынан жеңіл, қатаңдығы мен беріктігі жоғары, өзі арзан конструкциялардың жобасын есептеу болып табылады.
Сонымен, «Материалдар кедергісі» деп машина мен конструкциялардың бөліктерінің беріктігі, қатаңдығы және орнықтылығы туралы ғылымды айтамыз.
Беріктікдеп конструкцияның немесе оның жеке элементтерінің сыртқы күш әсеріне қирамай қарсыласу қабілетін айтады.
Қатаңдықдеп конструкция мен оның элементтерінің деформацияға қарсыласу қабілетін атайды.
Орнықтылықдеп конструкцияның немесе оның элементтерінің белгілі алғашқы серпімді тепе-теңдік күйін сақтау қабілетін айтады.
Есептеу денелерінің түрлері. Инженерлік практикада кездесетін сан алуан конструкция элементтері пішіндері мен өлшемдеріне байланысты жинақталып, төмендегідей қарапайым түрлерге жіктелген:
1 Білеу (брус) - екі өлшемі үшін,шісінен әлдеқайда кіші дене (2.1, а, b - сурет). Дербес жағдайда білеудің көлденең қимасының ауданы тұрақты, ал өсі түзу сызықты болуы мүмкін (2.1, b - сурет).

Өсі түзу сызықты білеуді стержень деп атайды.
Білеудің өсі дегеніміз көлденең қималардың ауырлық центрлерінің геометриялық орны (2.1, c - сурет).
2 Пластина – ара қашықтығы басқа өлшемдеріне қарағанда өте кіші, екі жазық бетпен шектелген дене (2.2, а - сурет).
3 Қабықша - ара қашықтығы басқа өлшемдеріне қарағанда әлдеқайда кіші болатын екі қисық сызықты беттермен шектелген дене (2.2, b - сурет).
 4 Массив - үш өлшемдері өзара шамалас дене (2.2, с - сурет).
4 Массив - үш өлшемдері өзара шамалас дене (2.2, с - сурет).
«Материалдар кедергісі» пәнінде қатаңдығы жеткілікті, аз деформацияланатын, көбінесе көлденең қималары тұрақты, білеу тәріздес жұмыр денелер немесе олардан құрылған қарапайым жүйелер қарастырылады.
Сыртқы күштер. Материалдар кедергісі есептерін шешкенде, ең алдымен конструкция элементтеріне әсер ететін сыртқы күштің шамасы мен түсу сипатын анықтап алу қажет. Белгілідей, сыртқы күш деп денелердің бір- бірімен әсерін, демек, сол конструкция элементтерінің өзара әсерін де айтады. Сол сияқты берілген конструкция элементінің басқа денемен әсері қарастырылған элемент үшін, сыртқы күш болып табылады. Мысалы, шамға құйылған жермайдың салмағы шан орнатылған тұғырға түседі, одан тұғырдың аяқтары арқылы іргетасқа түседі. Элементтің өз салмағы да сыртқы күшке жатады.
Сыртқы күштер көлемдік және беттік болып бөлінеді. Беті арқылы берілетін сыртқы күшбеттік, ал көлемі арқылы берілетін сыртқы күш көлемдік күш деп аталады.
Беттік күштер қадалғаннемесе таралған күш болуы мүмкін.
Қадалған күш деп, конструкция элементтеріне өз өлшемдерімен салыстырғанда өте шағын аудан арқылы берілетін күшті айтады. Қадалған күштің өлшем бірлігі ньютон (Н), килоньютон (кН), меганьютон (МН). Мысалы, тісті берілістегі тістердің бір-біріне әсері. Ауданның өте шағындығына байланысты қадалған күш әдетте денеге нүкте арқылы беріледі деп есептелінеді.
Таралған күш деп не элементтің барлық көлеміне (көлемдік күш), не белгілі бір ауданына (жазықтық күш), не белгілі бір ұзындыққа (сызықтық немесе бойлық жүк) үздіксіз түсірілген күшті айтады. Ол қарқындылығымен сипатталады. Қарқындылық деп күштің бірлік көлемге немесе бірлік ауданға немесе бірлік ұзындыққа түсірілген шамасын айтады. Қарқындылық латынша q әрпімен белгіленеді, сәйкесінше таралған күштердің өлшем бірлігі: көлемдік күш - 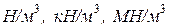 ; жазықтық күш -
; жазықтық күш - 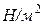 ;
; 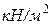 ,
, 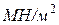 ;сызықтық немесе бойлық күш -
;сызықтық немесе бойлық күш - 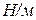 ;
; 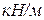 ,
, 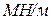 .
.
Бұл күштер таралу заңдылықтарына байланысты біркелкі таралған тұрақты және бірқалыпсыз таралған айнымалы күштер деп жіктеледі. Біркелкі таралған тұрақты күштің кез келген нүктедегі қарқындылығы өзара тең, ал бірқалыпсыз таралған айнымалы күштің қарқындылығы әр түрлі.
Денеге тұтас көлемі арқылы берілетін күштер қатаң түрде үздіксіз біркелкі тараған деп қарастырылады.
Көлемдік күшке мысал ретінде дененің салмағын, жазықтық күшке – будың қазан қабырғасына қысымын, сызықтық күшке – ені ұзындығынан өте аз арқалыққа ұзына бойлы түсірілген күшті келтіруге болады.
Сыртқы күш әсер ететін уақытына байланысты да екі топқа бөлінеді: тұрақты күшжәне уақытша күш.
Тұрақты күш деп мөлшері мен бағыты өзгермейтін күшті айтады. Егер денеге түскен күштердің шамасы немесе бағыты уақытқа байланысты өзгеріп отырса, ондай күштерді айнымалы күштер деп атайды.
Сыртқы күштерді статикалық және динамикалықкүштер деп те топтастыруға болады.
Статикалық күш деп өзінің шамасын немесе түсу нүктесін баяу жылдамдықпен өзгертетін, осы жағдайда туындауы мүмкін үдеуді ескермеуге болатын күшті атайды. Мұндай күш әсерінен конструкцияның және оның элементтерінің тербелісі мардымсыз аз болады.
Динамикалық күш деп уақытқа байланысты үлкен жылдамдықпен өзгеретін күшті айтады. Мұндай күштің әсерінен конструкция немесе оның элементтері елеулі тербелістерге ұшырайды. Тербеліс жылдамдығының өзгеруіне байланысты конструкцияда пайда болатын, оның массасы мен үдеуінің көбейтіндісіне тура пропорционал екпін күші шамасы жағынан конструкцияда тербеліс тудырушы сыртқы күштің шамасынан бірнеше есе үлкен болуы мүмкін.
Динамикалық күштер соққы, айнымалы–қайталанбалы және т. б. түрлерге жіктеледі.
Соққы күш деп кинетикалық энергиясы бар қозғалыстағы дененің екінші бір денеге соқтығысуы арқылы берілетін күшті айтады.
Айнымалы–қайталанбалыкүштер деп машина бөлшектеріне уақытқа тәуелді, периодты түрде қайталанып түсетін күштерді атайды. Мысалы, қозғалыстағы машинаның шатун, білік сияқты бөліктеріне немесе темір жол вагонының өсіне түсетін күштер айнымалы – қайталанбалы күштерге жатады.
Жалпы жағдайда күш уақытқа тәуелді күрделі заңдылықпен өзгеруі мүмкін.
Деформациялар. Қандай дене болмасын сыртқы күш әсерінен өздерінің өлшемдері мен пішіндерін өзгертеді, яғни деформацияланады, ақырында күштің бір жеткілікті үлкен шамасында қирайды, бірнеше бөлшектерге бөлінеді. Денелердің өлшемдері мен пішіндерінің өзгеруіндеформация деп атайды. Ол материалдың атомдарының ара қашықтықтарының өзгеруі мен атом блоктарының орын ауыстыруы салдарынан туындайды.
Сыртқы күш әсері жойылғанда, денедегі деформация да жойылса, ондай деформацияны серпімді деформациядеп атайды, ал дененің күш әсері жойылғаннан кейін өзінің алғашқы қалпына келу қасиеті серпімділік деп аталады.
Қалдық немесе пластикалық деформациядеп денеде сыртқы күш әсері жойылғаннан кейін де сақталып қалатын деформацияны айтады, ал материалдың қалдық деформация беретін қасиетін пластикалық деп атайды.
Дененің сызықты өлшемдерінің өзгеруін сызықтық деформация,ал бұрыштық өлшемдерінің өзгеруін бұрыштық деформация деп айтады.

Ішкі күштер. Қию әдісі. Жоғарыда айтылғандай, сыртқы күш әсерінен денелер деформацияланады. Денелердің атомнан тұратыны, ал атомдар өзара атомдық күшпен байланысып тепе – теңдік күйде болатыны физика курсынан мәлім. Дене деформацияланған кезде атомдардың ара қашықтығы өзгереді. Осының салдарынан атомдық күш қандай да бір қосымша әсерлесу күшіне – серпімді күшке өзгереді. Қосымша күш атомдарды алғашқы күйіне келтіруге тырысады. Бұл атомдардың қосымша өзара әсерлесу күші материалдар кедергісі ғылымындаішкі күш деп аталады. Ол конструкция элементтерінің сыртқы күш әсеріне қарсыласу қабілеттігін көрсетеді. Сонымен, ішкі күштің өзгеру мөлшері, сыртқы күштің өзгеру мөлшерімен тең болғанда ғана, конструкция элементтері жұмыс істеу қабілеті мен тепе–теңдік күйін сақтай алады.
Сыртқы күштердің ұлғайуымен ішкі күштердің де өсетіні, әрине, айқын. Бірақ ішкі күштердің шексіз ұлғайуы мүмкін емес, қандай да бір мезетте белгісіз бір нүктенің төңірегінде сыртқы күштерді теңестіре алмауы мүмкін. Бұл күштердің өзара теңсіздігі конструкцияның қирап сынуына немесе орнықтылығын жоғалтуына әкеліп соқтыратыны мәлім. Сондықтан да, ішкі күштің шамасын білмей, машиналар мен конструкциялардың беріктігін бағалау мүмкін емес.
Ішкі күштерді табу үшін, қию әдісі қолданылады. Бұл әдіс «Дене тепе–теңдік күйде тұрса, онда оның кез келген бөлігі де тепе–теңдік күйде болады» деген механика заңдылығына негізделген. Қию әдісінің маңызы мынада. Білеу пішінді, қандай да бір денені қарастырайық. Оған теңестірілген жүйені құратын сыртқы 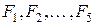 күштері әсер етсін делік (2.3, а - сурет). Бізді қызықтыратын брустың А–А қимасын қарастырайық. Ол үшін дене осы қимада
күштері әсер етсін делік (2.3, а - сурет). Бізді қызықтыратын брустың А–А қимасын қарастырайық. Ол үшін дене осы қимада 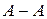 жазықтығымен қиылып, сол бөлігі
жазықтығымен қиылып, сол бөлігі 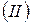 алынып тасталған деп елестетейік (2.3, b - сурет). Егер бүтін дене сыртқы күш әсерінен тепе-теңдікте болса, онда оның әрбір бөлігі де тепе-теңдікте болады. Бұл жағдайда әрбір бөлікке өздеріне түсірілген сыртқы күштермен қатар
алынып тасталған деп елестетейік (2.3, b - сурет). Егер бүтін дене сыртқы күш әсерінен тепе-теңдікте болса, онда оның әрбір бөлігі де тепе-теңдікте болады. Бұл жағдайда әрбір бөлікке өздеріне түсірілген сыртқы күштермен қатар 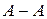 қимасындағы материал бөлшектерінің өзара әсерінің ішкі күштері де әсер етеді деп қарастыру қажет (2.3, b - сурет). Осы ішкі күштер қарастырылып отырылған
қимасындағы материал бөлшектерінің өзара әсерінің ішкі күштері де әсер етеді деп қарастыру қажет (2.3, b - сурет). Осы ішкі күштер қарастырылып отырылған 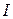 бөлікке алып тасталған
бөлікке алып тасталған 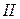 бөліктің әсерін көрсетеді. Қимадағы ішкі күштер үздіксіз жайылып таралып беріледі. Жалпы жағдайда олардың әсер ету бағыттары мен шамалары белгісіз, бірақ кез келген сыртқы күштер жүйесі сияқты ішкі күштер жүйесін де бір нүктеге келтіруге болады, атап айтқанда, қиманың ауырлық центріне. Нәтижесінде
бөліктің әсерін көрсетеді. Қимадағы ішкі күштер үздіксіз жайылып таралып беріледі. Жалпы жағдайда олардың әсер ету бағыттары мен шамалары белгісіз, бірақ кез келген сыртқы күштер жүйесі сияқты ішкі күштер жүйесін де бір нүктеге келтіруге болады, атап айтқанда, қиманың ауырлық центріне. Нәтижесінде 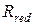 бас вектор мен
бас вектор мен 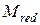 бас момент алынады (2.3, c - сурет).
бас момент алынады (2.3, c - сурет).
Бас нүктесі ауырлық центрде жататын координаттар жүйесін тұрғызып, бас вектор мен бас моментті өстерге жіктеп, үш күш пен үш моменттен тұратын құраушыларын аламыз. Бұл құраушы күштер мен моменттер брустың қимасындағы ішкі күш факторларынемесеішкі күш компоненттері деп аталады (2.3, d - сурет). Олардың әрқайсысының өз аттары бар: 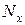 - көлденең қимаға перпендикуляр бойлық өс бойымен әсер етеді, сондықтан ол бойлық күш;
- көлденең қимаға перпендикуляр бойлық өс бойымен әсер етеді, сондықтан ол бойлық күш; 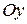 және
және 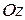 өстеріне параллель әсер ететін
өстеріне параллель әсер ететін 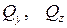 ішкі күштері - көлденеңнемесе жанама күштер;
ішкі күштері - көлденеңнемесе жанама күштер; 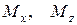 моменттері - ию моменттері;
моменттері - ию моменттері; 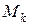 моменті - бұрау моменті.
моменті - бұрау моменті.
Дененің оң 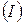 немесе сол
немесе сол 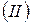 бөліктеріне түсірілген ішкі және сыртқы күштері өзара тепе–теңдік күйде болады. Сондықтан, ішкі күштерді дененің кез келген бөлігі үшін, құрылған тепе–теңдік теңдеулерінен анықтауға болады.
бөліктеріне түсірілген ішкі және сыртқы күштері өзара тепе–теңдік күйде болады. Сондықтан, ішкі күштерді дененің кез келген бөлігі үшін, құрылған тепе–теңдік теңдеулерінен анықтауға болады.
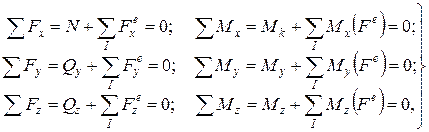 (2.1)
(2.1)
мұндағы
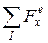 ,
, 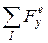 ,
, 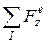 - білеудің қарастырылып отырған бөлігіне әсер ететін сыртқы күштердің, сәйкесінше
- білеудің қарастырылып отырған бөлігіне әсер ететін сыртқы күштердің, сәйкесінше 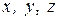 өстеріне проекцияларының алгебралық қосындылары;
өстеріне проекцияларының алгебралық қосындылары;
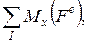
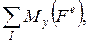
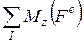 - білеудің қарастырылып отырған бөлігіне әсер ететін сыртқы күштердің, сәйкесінше
- білеудің қарастырылып отырған бөлігіне әсер ететін сыртқы күштердің, сәйкесінше 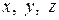 өстеріне қарағандағы моменттерінің алгебралық қосындылары.
өстеріне қарағандағы моменттерінің алгебралық қосындылары.
Бірінші бағанадағы үш теңдеуден 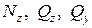 ішкі күштері, ал екінші бағанадағы үш теңдеуден
ішкі күштері, ал екінші бағанадағы үш теңдеуден 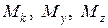 ішкі моменттері анықталады.
ішкі моменттері анықталады.
(2.1) теңдеулерінен тұжырымдалатын ішкі күштерді анықтаудың ережелері кейінірек қарастырылады.
Дененің оң және сол бөліктерінің көлденең қима ауданы арқылы бір–біріне тигізетін әсері, яғни ішкі күштері шамасы жағынан тең, бағыты жағынан қарама-қарсы (2.4 – сурет).
 Сонымен, ішкі күш әсерлерін анықтау үшін, мыналарды орындау қажет:
Сонымен, ішкі күш әсерлерін анықтау үшін, мыналарды орындау қажет:
1) ішкі күштер ізделініп отырған қима арқылы жүргізілген жазықтықпен дене кесіліп, екіге бөлінеді;
2) бөліктердің бірі алынып тасталады;
3) қимаға қалдырылған бөлікке әсер ететін сыртқы күштерді теңестіретін ішкі күштер түсіріледі, яғни алып тасталған бөліктің қалдырылған бөлікке әсері ішкі күштермен көрсетіледі;
4) қалдырылған бөлікке тұрғызылған тепе-теңдік теңдеулерінен ішкі күш факторлары анықталады.
Дербес жағдайда білеудің көлденең қимасы мынадай күйде болуы мүмкін:
1) тек қана бойлық күш 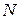 әсер етеді. Мұндай жағдайдағы болатын деформацияны, егер
әсер етеді. Мұндай жағдайдағы болатын деформацияны, егер 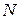 күші қимадан сыртқа қарай бағытталған болса,созылудеп, ал
күші қимадан сыртқа қарай бағытталған болса,созылудеп, ал 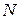 күші қимаға қарай бағытталған болса, онда сығылу деп атайды;
күші қимаға қарай бағытталған болса, онда сығылу деп атайды;
2) тек қана 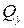 немесе
немесе 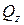 көлденең күштері әсер етеді. Бұл жағдайда ығысу немесе кесілу деформациялары туындайды;
көлденең күштері әсер етеді. Бұл жағдайда ығысу немесе кесілу деформациялары туындайды;
3) тек қана бұрау моменттері 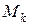 әсер етеді. Мұндағы деформациябұралу деп аталады;
әсер етеді. Мұндағы деформациябұралу деп аталады;
4) тек қана 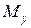 немесе
немесе 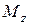 ию моменттері әсер етеді. Бұл жағдайдағы деформация таза иілу деп аталады. Егер тек қана
ию моменттері әсер етеді. Бұл жағдайдағы деформация таза иілу деп аталады. Егер тек қана 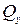 пен
пен 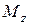 немесе
немесе 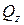 пен
пен 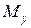 ішкі күштері әсер етсе, деформация көлденең иілуделінеді;
ішкі күштері әсер етсе, деформация көлденең иілуделінеді;
5) бірнеше ішкі күштер әсері, мысалы, бұралу және ию моменттері әсері. Мұндай жағдайлар күрделі деформация немесе күрделі қарсыласу деп аталады.
Кернеулер. Сыртқы теңестірілген күштер жүйесі түсірілген стерженьді қарастырайық. Жоғарыда айтылғандай, ойша қиып алынған оның әрбір бөлігі өздеріне түсірілген сыртқы күштер мен қимадағы ішкі күштері әсерінен тепе-теңдікте болады (2.3, b - сурет). Стерженьнің алынып тасталған бөлігінің әсерін көрсететін ішкі күштер қимада үздіксіз таралады.
Кернеулі күйі деп аталатын, жүктелген стержень материалы жағдайының ең маңызды сипаттамасы болып ішкі күштердің қарқындылығы есептеледі, яғни серпімді күштердің қима ауданының бірлігіне шаққандағы шамасы. Бұл шама кернеудеп аталады. Материалдың кернеулі күйін зерттеу, яғни жүктелген конструкция элементтерінің кез келген қимасындағы кернеуді анықтау материалдар кедергісінің ең маңызды есептерінің бірі болып табылады.
Серпімді күштердің таралу заңдылығын зерттеу үшін, қима бетіндегі кез келген нүкте төңірегіндегі, ауданы шексіз кіші 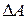 болатын элементар қиманы бөліп алайық. Осы элементар қимаға түсетін серпімді күштердің тең әсерлі күші
болатын элементар қиманы бөліп алайық. Осы элементар қимаға түсетін серпімді күштердің тең әсерлі күші 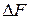 болсын делік (2.5, а - сурет). Ішкі күштердің тең әсерлі күші
болсын делік (2.5, а - сурет). Ішкі күштердің тең әсерлі күші 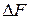 - тің шексіз кіші аудан
- тің шексіз кіші аудан 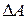 - ға қатынасы жүргізілген қиманың берілген нүктесіндегі орташа кернеу деп аталады.
- ға қатынасы жүргізілген қиманың берілген нүктесіндегі орташа кернеу деп аталады.
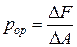 . (2.2)
. (2.2)
Берілген нүктедегі ішкі күштердің қарқындылығын неғұрлым дәлірек білгіміз келсе, соғұрлым элементар қиманы бөліп алуымыз қажет. Элементар қиманың шексіз кіші ауданы нөлге ұмтылғандағы көрсетілген қатынастың шегі берілген нүктедегі толық кернеуді немесе нақты кернеуді береді (2.5, b – сурет)

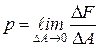 . (2.3)
. (2.3)
Кернеудің өлшем бірлігі: 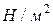 ,
, 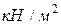 ,
, 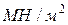 немесе
немесе 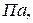
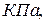
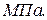
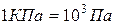 ,
, 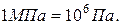
Қарастырылған қимадағы берілген нүктенің кернеуі векторлық шама, ол бағытымен және шамасымен анықталады. Жалпы алғанда, берілген нүктедегі кернеу элементар қиманың жазықтығына кез келген 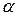 бұрышымен түсуі мүмкін (2.6, а – сурет).
бұрышымен түсуі мүмкін (2.6, а – сурет).
Толық кернеудің көлденең қима жазықтығына перпендикуляр 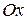 өсіне түсірілген проекциясы тік кернеудеп аталып,
өсіне түсірілген проекциясы тік кернеудеп аталып, 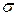 әрпімен белгіленеді, ал қима бетіне түсірілген проекциясы жанама кернеу деп аталып,
әрпімен белгіленеді, ал қима бетіне түсірілген проекциясы жанама кернеу деп аталып, 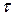 әрпімен белгіленеді (2.6, а - сурет).
әрпімен белгіленеді (2.6, а - сурет).
Әлбетте, тік және жанама кернеулердің шамалары
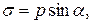
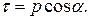 (2.4)
(2.4)
Демек, толық кернеудің шамасы
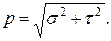 (2.5)
(2.5)
Сыртқы күштердің әсер ету ерекшеліктеріне байланысты жанама кернеудің бағыты әр түрлі болуы ықтимал. Сондықтан оны 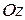 ,
, 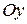 өстеріне параллель
өстеріне параллель 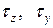 құраушыларына жіктеледі (2.6, b - сурет).
құраушыларына жіктеледі (2.6, b - сурет).
Материалдар денеге түсірілген жүктемеге кернеудің белгілі бір шамасына дейін төтеп бере алады, ал одан кейін бұзылып қирайды. Мұндай кернеулер беріктік шегі немесе уақытша қарсыласу деп аталады. Әр түрлі материалдардың беріктік шектері де әр түрлі және олардың шамалары әрбір жеке жағдайда тәжірибелік жолмен анықталады.
Материалдар кедергісінің негізгі жорамалдары. Материалдар кедергісінде конструкция элементтерін есептеу күрделі болғандықтан, оны іс жүзінде оңай және ыңғайлы түрде шешу үшін, материалдардың құрылымы, қасиеттері туралы, деформациялар мен күштер және т. б. деректер туралы бірнеше жорамалдар қолданылады.
Бұл жорамалдар ескеріліп алынған есептеу нәтижелерінің дұрыс екені, оларды инженерлік практикада кеңінен қолдануға болатыны тәжірибе жүзінде дәлелденген. Төменде материалдар кедергісі курсында кездесетін негізгі жорамалдар келтірілген:
1 Материалдың тұтастығы туралы жорамал. Материал дене пішімін толық толтырады, яғни дене үздіксіз тұтас орта деп қарастырылып, оның дискреттік (атомдық) құрылымы ескерілмейді.
2 Материалдың біртектілігі және изотроптылығы туралы жорамал. Материалдардың кез келген көлемдегі және кез келген бағыттағы механикалық қасиеттері бірдей.
Машина өндірісінде қолданылатын конструкциялық материалдардың көпшілігі біртекті. Ал, құрылыста қолданылатын ағаш, бетон және композитті пластмассалар сияқты т. б. материалдар біртекті емес.
Әр түрлі бағыттағы механикалық қасиеттері бірдей емес материалдарды анизотропты материалдар деп атайды.
Материалдарды изотропты деп болжау кейбір жағдайларда қолданылмайды. Мысалы, анизотропты материалдарға ағаш жатады, өйткені оның талшық бойы бағытындағы және талшыққа кесе көлденең бағыттағы қасиеттері әр түрлі, арматураланған материалдар және т.т.
3 Деформациялардың кішкентайлығы туралы жорамал.Деформацияланатын дененің өлшемдеріне қарағанда деформация өте кішкентай аз шама.
4 Материалдардың толық серпімділігі туралы жорамал.Барлық денелер абсолют серпімді деп болжанады. Шын мәнінде бар денелерді шартты түрде жүктеменің қандай да бір шамасына дейін серпімді деп айтуға болады және осы жәйтті материалдар кедергісінің есептеу формулаларын пайдаланғанда ескерген жөн.
5 Деформация мен жүктеменің сызықтық тәуелділігі туралы жорамал.Көптеген материалдардың деформациялануы кезінде деформация мен жүктеменің тура пропорционалдығы жөніндегі Гук заңының ақиқаттығы туралы болжам.
6 Күш әрекеттерінің тәуелсіздік принципі. Бұл принцип бойынша денедегі топ күштер әсерлерінің нәтижесі сол топтағы жеке күштердің әсерлерінің нәтижелерінің қосындысына тең. Яғни, күш тобының әсерінен жүйеде пайда болған деформация сол топтағы жеке күштердің әсерлерінен пайда болған деформациялардың қосындысына тең.
 7 Сен–Венан принципі. Бұл принцип бойынша, конструкция элементінің сыртқы күш түсірілген жерінен жеткілікті қашықтықта жатқан нүктеде пайда болған ішкі кернеу сыртқы күшті түсіру әдісіне байланысты емес.
7 Сен–Венан принципі. Бұл принцип бойынша, конструкция элементінің сыртқы күш түсірілген жерінен жеткілікті қашықтықта жатқан нүктеде пайда болған ішкі кернеу сыртқы күшті түсіру әдісіне байланысты емес.
Осы принципке арқа сүйеп, көптеген жағдайда бір күш жүйесін, оған статикалық эквивалентті, басқа күш жүйесімен алмастыруға болады, нәтижесінде есепті шешу жеңілдейді. Мысалы, көп тіректі темір жол рельсінің есептеу схемасын құрғанда, дөңгелектен рельске кішігірім аудан арқылы берілетін бірқалыпсыз таралған күшті нүкте арқылы берілетін қадалған күшпен ауыстыруға болады (I.2.7 - сурет).
Лекций
Дата добавления: 2017-01-13; просмотров: 7552;
