Бойлық созылу мен сығылу

Бойлық және ендік деформациялар, кернеу. Гук заңы. Көлденең қимасының ауданы тұрақты 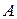шамалы ұзындығы 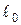призмалық білеуді алып, бетіне тік және көлденең бағытта түзулер жүргізіп, шамалары жағынан тең, бағыттары қарама–қарсы екі бойлық күшпен әсер етейік (2.8, а - сурет). Күш әсерінен білеу созылу не сығылу деформациясына ұшырайды. Бұл екі деформацияларды бірге қарастыруға болады, себебі білеу созғанда ұзарса, қысқанда (сығылғанда) қысқарады. Білеу ұзындығының қысқаруын теріс таңбалы ұзару деп те қарастыруға болады.

Созылу деформациясымен шынжырларды, арқандарды, болттарды, әр түрлі аспаларды есептеуде кездессек, сығылу деформациясы іргетастар мен тіректерді есептеуде қарастырылады.

Білеуге әсер етуші күштерді созушы күштер деп қарастырсақ, (2.8, b - сурет) онда білеудің ұзындығы

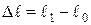(2.6)

шамасына ұзарады (созылады), ал ені

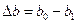(2.7)

шамасына қысқарады (сығылады).

Білеудің бастапқы ұзындығының ұзару шамасын 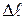- абсолют ұзару, ал енінің қысқару шамасын 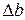- абсолют қысқару деп атаймыз.

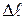немесе 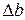шамалары бойынша білеудің деформациялану қабілетін сипаттауға болмайды, өйткені абсолют ұзару мен қысқару білеуге әсер етуші күшпен қатар білеудің бастапқы өлшем бірліктеріне байланысты. Сондықтан созылған немесе сығылған білеудің деформациялану шамасын сипаттау үшін, абсолют ұзарудың білеудің алғашқы ұзындығына, ал абсолют қысқарудың білеудің алғашқы еніне қатынастарын алған дұрыс, яғни

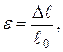(2.8)

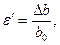(2.9)

мұндағы 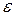- бойлық салыстырмалы деформациясы деп, ал 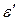- ендік салыстырмалы деформация деп аталады. (2.8) және (2.9) формулаларына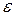н мен 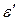өлшем бірліксіз шамалар екенін көреміз.

Көптеген тәжірибе нәтижелері әр түрлі материалдар үшін, ендік салыстырмалы деформацияның бойлық салыстырмалы деформацияға қатынасының тұрақты шама екенін көрсетеді. Бұл қатынастардың абсолют шамасы 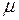деп белгіленеді

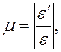(2.10)

мұндағы 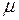- материалдың қасиетін сипаттайды да, ендік деформация коэффициенті немесе Пуассон коэффициенті деп аталады. Бұл коэффициенттің мәні әр түрлі материалдар үшін, тәжірибелік жолмен анықталады. Барлық изотропты материалдардың Пуассон коэффициентінің мәні 0 – 0,5 аралығында жатады, мысалы, тығын үшін, 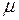нөлге жақын; көксағыз – 0,5 жақын; шойын – 0,25; болат – 0,33; мыс – 0,34; жез – 0,42-ге жақын.

(2.10) өрнегі білеудің сығылу деформациясына да жарамды (ақиқатты).

Қарастырылып отырған білеу бетіндегі өзара перпендикуляр түзулердің күш әсерінен кейін де өзара перпендикуляр күйінде қалатынын көреміз (2.8, b - сурет). Көлденең түзулердің өзара параллель қалпында орындарын ауыстыратыны да байқалады. Бұл жағдай білеудің деформацияға дейінгі жазық көлденең қималары деформациядан кейін де жазық көлденең күйінде қалады деген тұжырымды береді. Бұл тұжырым Бернулидің жазық қималар жорамалы деп аталады.

Білеудің көлденең қималарына әсер етуші күштің шамасын анықтау үшін, қима әдісін пайдаланып, 1–1 жазықтығымен білеуді ойша екі бөлікке бөліп (2.9, а - сурет), оң бөлігін алып тастап, сол бөлігінің тепе–теңдігін қарастырайық. Қарастырушы бөліктің тепе-теңдік жағдайы сақталуы үшін, 1–1 қима жазықтығына тік бағытталған бойлық серпімді күштермен әсер етейік (2.9, b - сурет).

Бұл күштер қарастырылушы бөлікке алынып тасталған бөліктің әсерін сипаттайды. Білеудің қимасындағы шексіз кішкене аудандарға әсер етуші 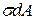ішкі серпімді күштердің тең әсерлі күшін, 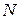бойлық күш деп атайды (2.9, c - сурет).

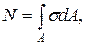(2.11)

мұндағы 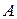– білеудің көлденең қимасының ауданы.

Бұл тең әсер етуші 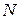күші білеу өсі бойымен әсер етеді және шама жағынан сыртқы әсер етуші 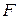күшін,е тең,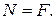

Бойлық созушы күш оң, ал сығушы күш теріс таңбалы деп саналады. Бойлық күштің білеу бойындағы өзгеру заңдылығын кескіндейтін график бойлық күш эпюрасы деп аталады.

Жоғарыда атап өтілген Бернулидің жазық қималар жорамалына сүйене отырып, көлденең қималардағы тік кернеулер қима ауданында біркелкі жайылып әсер етеді деп тұжырымдасақ, тік кернеудің шамасы

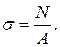(2.12)

Бойлық күш сияқты, созушы кернеудің таңбасы – оң, ал сығушы кернеудің таңбасы – теріс, өлшем бірлігі -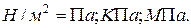

Роберт Гук 1660 жылы тәжірибе жүзінде білеудің абсолют ұзаруы (сығу жағдайында - қысқаруы) мен оған әсер етуші күштің арасында белгілі байланыс барын ашты. Ол білеудің серпімді абсолют ұзаруының білеуге әсер етуші күш пен білеу ұзындығына тура пропорционалдығын, ал қима ауданына кері пропорционалдығын және оның шамасы материалдың қасиетіне де байланыстылығын тапты. Бұл заңдылық Гук заңы деп аталады

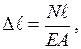(2.13)

мұндағы 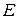- материалдың бірінші текті серпімділік модулі, ол тәжірибе жүзінде анықталады. Серпімділік модулі - материал қасиетін сипаттайтын коэффицент; өлшем бірлігі кернеудің өлшем бірлігіндей. 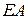– білеудің созылғандағы немесе сығылғандағы қатаңдығы деп аталады, ол материалдың созылуға немесе сығылуға қарсыласу қабілеттігін сипаттайды.

Кейбір материалдардың серпімділік модулі (МПа): ақ, сұр шойын - 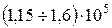; көміртекті болат - 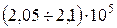; мыс – 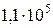; жез - 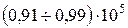, алюминий - .

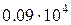Енді 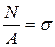және 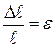екендігін ескере отырып (2.13) өрнегін түрлендірейік, сонда

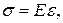(2.14)

яғни материалдың серпімділік деформация шегі аралығындағы бойлық салыстырмалы деформациялардың кернеулерге тура пропорционалдық заңдылығын (Гук заңын) аламыз.

Гук заңының бұл түрі конструкция элементтерінің деформациялануы мен беріктігін сынақ жүзінде зерттеулерде кеңінен қолданылады.

Бұл жерде кернеудің деформацияға тура пропорционал заңдылығының әр материалдар үшін, кернеу шамасының белгілі бір мөлшерден аспаған жағдайда ғана орындалатынын айта кеткен жөн. Кернеу мен салыстырмалы деформация аралығындағы тура пропорционал заңдылық орындалатын кернеудің ең үлкен шамасын пропорционал шегі деп атап, 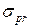деп белгілейміз. Әр түрлі материалдар үшін, 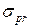тәжірибемен анықталады. Сонымен Гук заңы пропорционал шегі аралығанда ғана сақталады.

Мүмкіндік кернеу. Беріктік қоры коэффициенті. Инженерлік құрылыстар мен конструкцияларда пайдаланылатын материалдарды екі топқа бөлуге болады: өте аз деформациядан кейін қирайтын морт материалдар, мысалы: шойын, болат; пішіндері мен өлшемдерінің үлкен өзгеру шамаларынан кейін қирайтын пластикалық материалдар, мысалы, болат, мыс. Созушы және сығушы күш әсерлеріне морт материалдар өте төзімсіз, сонымен қатар жергілікті кернеулерге сезімтал келеді. Пластикалық материалдарда айтылғандай кемшіліктер жоқ. Олар созылуға және сығылуға бірдей қарсыласады.

Әр материал кернеулерінің шектік шамалары (аққыштық, беріктік және қажу шектері) механикалық сынақтармен анықталады. Кернеулердің шектік шамаға жетуі конструкция элементтерінің қирауына не оларда мөлшерден тыс қалдық деформациялардың пайда болуына себепкер болады, яғни материалдардың қауіпті күй деп аталатын жағдайын туғызады. Материалдардың осы күйге сәйкес кернеу шамасын қауіпті кернеу деп атаймыз.

Конструкцияның қауіпсіз жұмыс істеуі үшін, оның элементтеріндегі кернеулердің ең үлкен шамасы қауіпті кернеуден біршама кем болуы қажет. Ол материалдың қауіпті күйінің болмауын қамтамасыз етеді. Сондықтан да кернеудің қауіпсіз не мүмкіндік кернеу деп аталатын шамасын анықтау, жобалау есептерінде үлкен маңызды орын алады. Сонымен, жобаланылатын, есептелінетін конструкция элементінің сенімді және ұзақ жұмыс істеуін қамтамасыз ететін кернеудің ең үлкен шамасын мүмкіндік кернеу деп атаймыз. Бұл кернеу, әрине, қауіпті кернеудің қайсыбір бөлігіне тең болады. Мүмкіндік кернеудің қауіпті кернеуден неше есе кіші екендігін көрсететін 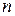- саны қауіпсіздік коэффициенті не беріктік қоры коэффициентідеп аталады.

Мүмкіндік кернеу әр материалдардың қауіпті күйін және соған сәйкес қауіпті кернеуін туғызатын күш әсерінің түріне және материалға байланысты.

Тұрақты не соғу күш әсерінде пластикалық материалдардың қауіпті күйі мөлшерден тыс қалдық дефомацияның (аққыштық) пайда болуымен сипатталады, морт материалдар үшін, – сызаттың пайда болуы, не материалдың қирауы. Айнымалы қайталанбалы күш әсерінде материалдардың қауіпті күйі қажудың микроскопиялық сызаттардың пайда болып және оның дамуымен сипатталады.

Осы әр түрлі жағдайларда қауіпті күйдің туындауына сәйкес келетін қауіпті кернеу:

а) пластикалық материал үшін, аққыштық шегіне ;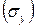

б) морт материал үшін, беріктік шегіне ;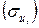

в) айнымалы – қайталанбалы күш әсерінде қажу шегіне 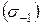тең болады.

Сонымен, мүмкіндік кернеу келесі формуламен анықталады.

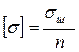, (2.26)

мұндағы: 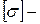мүмкіндік кернеу; 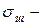қауіпті кернеу; 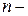беріктік қоры коэффициенті.

Пластикалық материалдардың беріктік қоры коэффициенті шамамен 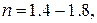ал морт материалдар үшін,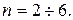

Созылған (сығылған) білеуді беріктікке есептеу. Машиналар мен құрылымдарды және олардың элементтерін жобалағанда, негізінен келесідей үш есептің түрлерімен кездесуге болады:

1) Жобалау есебі, яғни берілген күштердің шамасына сәйкес, таңдап алынған материалдан жасалынатын конструкция элементінің беріктігін, қатаңдығы мен жеткілікті төзімділігін қамтамасыз ететін қиманың ең аз өлшемдерін анықтау.

2) Беріктікті тексеру есебі, яғни белгілі күштердің шамасы мен конструкция элементтерінің көлденең қима өдшемдері бойынша элементтердегі нақтылы кернеулердің ең үлкен шамасын анықтап, мүмкіндік кернеумен салыстыру.

3) Жүк көтеру қабілетін анықтау есебі, яғни белгілі конструкция элементтерінің көлденең қима өлшемдері мен материалдарының мүмкіндік кернеуі бойынша конструкция элементтерінің жүк көтеру қабілетін анықтау.

Созылу мен сығылу деформацияның беріктік шарты келесі формуламен өрнектеледі.

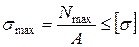, (2.27)

мұндағы: 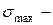нақтылы ең үлкен кернеу.

Беріктік шартына сүйеніп, созылу деформациясына сәйкес (пластикалық материалдар үшін,) жоғарыда қарастырылған үш есептің математикалық түрін өрнектесек, келесідей болады:

1) ;

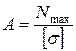2) ;

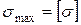3) .

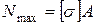Көлбеу жазықтықтардағы кернеулер. Кернеулі күйлер. Созылу мен сығылу деформациясын оқып үйренгенімізде, біз білеудің кез келген көлденең қимасындағы бірқалыпты таралған тік кернеуді қарастырдық. Енді білеудің көлбеу қимасындағы кернеулерін анықтайық.

Бойлық күш әсер еткен білеудің қандай да бір 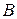нүктесін таңдап алайық (2.19, а - сурет) және оны білеуден тыс, жеке тіктөртбұрышты параллелепипед ретінде қарастырайық (2.19, b – сурет). Бернулли заңдылығына байланысты бұл параллелепипедтің білеудің көлденең қимасына параллель қабырғаларына тек тік кернеу, ал басқа қабырғаларына ешқандай кернеу әсер етпейтінін тұжырымдауға болады. Таңдап алынған элементті сыртқы нормаль білеудің бойлық өсімен 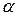бұрышын жасайтын жазықтықпен қиып, оң бөлігін алып тастап, сол бөлігінің тепе-теңдігін қарастырайық.

Егер 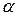бұрышы бойлық өстен сағат тіліне қарсы бағытта салынған болса, оң таңбалы деп, ал кері жағдайда теріс таңбалы деп саналады.

Қарастырылып отырылған бөлік өзінің тепе-теңдігін сақтайды, өйткені ауданы 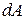бойлық өске перпендикуляр қабырғаға әсер ететін 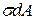күші, ауданы 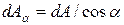көлбеу қимада әсер ететін бойлық өске параллель 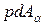күшімен теңестіріледі (2.19, c - сурет), яғни .

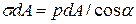Сондықтан, көлбеу қимаға әсер ететін, бірқалыпты жайыла таралған кернеу

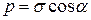(2.28)

тең болады, оны толық кернеу деп атайды.

Толық кернеуді көлбеу қиманың 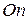нормалі мен 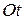жанамасы бағытындағы құраушыларына жіктейік (2.19, d -сурет):

.

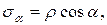
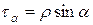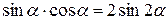екенін ескере отырып, бұл өрнекке (2.28)-ден 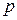-ның мәнін қойсақ

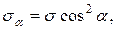(2.29)

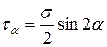. (2.30)

Сонымен, білеудің көлбеу қимасында тік және жанама кернеулер әсер етеді. Олардың шамалары белгілі күш әсерінде, қарастырылатын қимасының көлбеу бұрышына байланыстылығын көреміз.

Тік кернеу көлденең қимада ең үлкен мәнге ие болады, яғни (2.29) өрнегінен 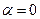болғанда, 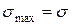, ал жанама кернеу ең үлкен мәніне көлденең қиманы 45⁰ бұрышпен көлбеу орналасқан қимада ие болады, яғни 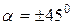болғанда, 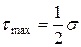екенін көреміз.

Енді қарастырылған көлбеу қимаға перпендикуляр, білеудің бойлық өсімен сыртқы нормалі 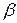бұрышын жасайтын көлбеу қиманы қарастырайық (2.20 - сурет). Бұл қимадағы кернеулерді анықтау үшін 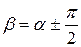екенін ескеріп, жоғарыда алынған (2.29) және (2.30) теңдіктерінен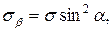 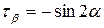деген өрнектерді аламыз.

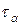және 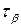өрнектерін салыстырсақ,

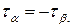(2.31)

екенін көреміз.

Яғни, өзара перпендикуляр аудандарда әсер етуші жанама кернеулер шамасы жағынан тең, бағыттары жағынан қарама-қарсы болады. Бұл тұжырым жанама кернеулердің қостық заңдылығы деп аталады.

Қарастырылушы қиманың сыртқы нормалімен бағыттас тік кернеулерді оң таңбалы деп есептейміз, егер жанама кернеудің бағыты сағат тілімен 90⁰ -қа бұрылған нормальмен бағыттас болса, оны да оң таңбалы деп есептейміз. Сонымен, созушы кернеулер оң таңбалы болса, сығушы кернеулер теріс таңбалы болады.

Алынған өрнектердің бойлық созылған (сығылған) білеуде жанама кернеуі нөлге тең алаңдардың болатындығын көреміз. Әрине, олар білеудің бойлық өсіне перпендикуляр және параллель қималар екені анық.

Лекция