Понятие средней величины. Виды средних величин

Наиболее распространенной формой статистических показателей является средняя величина.

Средняя величина характеризует тип явления. Она одна может охарактеризовать всю совокупность, отразив наиболее типичное для этой совокупности значение признака.

Или, средняя величина— типический уровень варьирующего признака. Как правило, средние характеризуют размер признака на единицу совокупности.

Средняя — одна из наиболее часто используемых в обыденной жизни статистических величин. Например, каждый рабочий зна­ет, что расчет отпускных производится исходя из средней зара­ботной платы за последние три месяца, поступающие в вузы — что такое пропускной балл и т.д.

В средних величинах погашаются индивидуальные различия еди­ниц совокупности, обусловленные влиянием различных условий развития отдельных единиц, значение средней отражает наиболее типичное значение. В отличие от средней, абсолютная величина, отражающая значение признака у отдельной единицы совокупно­сти, не позволяет сравнивать значение признака у единиц, относя­щихся к разным совокупностям.

Например, сравнивая возраст учащихся на дневном отделении университете с возрастом обучающихся в ИПК (Институт переподготовки квалификации), мы будем сравнивать не возраст отдельно взятого студента дневного отделения и студента ИПК, а средние значения возраста, рассчитанные по каждой совокупности.

Для того, чтобы средняя выполняла основное свое назначение — харак­теристика типа, при ее расчете должны выполняться следующие требо­вания:

— средняя должна быть рассчитана в пределах однородной сово­купности (качественно однородные совокупности позволяют получить метод группировок);

— расчет общих средних должен подкрепляться расчетом группо­вых средних;

— должна быть правильно выбрана единица совокупности, для ко­торой определяется средняя;

— должна быть обеспечена достаточная наполненность групп или совокупности, по которой рассчитывается средняя величина. Чем больше объем совокупности, тем более точной будет рассчитанная средняя (закон больших чисел).

Например, расчет средней прибыли по всем предприятиям торговли и общественного питания приводит к выводу об убыточности этих предприятий, однако, если рассчитать отдельно по каждой группе предприятий, то можно выделить типы предприятий, успешно работающих в этой области деятельности, например малые предприятия. На 01.07.97 г. доля прибыли, полученной этими пред­приятиями в общей прибыли данной отрасли, составила 377,78% (ресурсный центр малого предпри­нимательства).

Средние величины делятся на два больших класса:

— степенные средние;

— структурные средние.

К известным степенным среднимотносят среднюю арифметиче­скую, среднюю гармоническую, среднюю геометрическую, сред­нюю квадратическую.

Структурные средние —мода и медиана.

Общая формула средней степенной выглядит следующим образом:

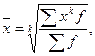
где 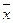— средняя;

х — индивидуальное значение варьирующего признака;

f — частота, которая показывает сколько раз встречается значе­ние осредняемого признака в данной совокупности. В зависимости от величины к определяется вид средней (табл. 2). Кроме то­го, вид средней определяется по сгруппированным или несгруп­пированным данным. Именно в том случае, если средняя величи­на определяется по несгруппированным данным, получают про­стую среднюю, если по сгруппированным — то взвешенную.

Смысл средней взвешенной можно проиллюстрировать на сле­дующем примере:

Пример. На продажу выставлен автомобиль. Ценовые оценки его стоимости потенциальными покупателями распределились следующим образом (в у.е.):

1000 у.е. 1 чел.

3500 у.е. 20 чел.

3600 у.е. 10 чел.

4000 у.е. 5 чел.

Если в расчетах использовать среднюю арифметическую простую, результат будет следующий:

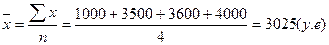
Если использовать среднюю арифметическую взвешенную, результат будет следующий:

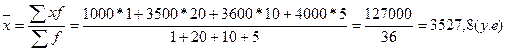
Результаты значительно отличаются друг от друга. Расчет при помощи средней арифметической взвешенной — более точный, так как учитывает вес. Наибольшая часть покупателей оценила стои­мость автомобиля в 3500 — 3600 у.е. — именно в этом интервале и оказалась средняя цена.