Средняя арифметическая, способы расчета
Если данные представлены в виде ряда распределения, то вопрос о выборе формы средней решается однозначно — средняя арифметическая. Этот вывод можно сделать, если вспомнить о том что ряд распределения есть не что иное как распределение значений варьирующего признака по частоте их появлений в совокупности.
Ряды распределения довольно часто встречаются в статистической практике. При этом варианта может быть задана в виде интервалов, если признак непрерывный, или в виде индивидуальных значений, если ряд дискретный. Для дискретных рядов расчет осуществляется по вышеприведенной формуле средней арифметической взвешенной. Для интервального ряда распределения задача расчета средней величины решается следующим образом. Предполагаем, что в пределах интервала значения признаков располагаются равномерно, поэтому середина интервала будет величиной, характеризующей весь интервал, то есть наиболее типичным для него значением. Данное предположение не всегда выполняется поэтому, чем меньше величина интервала, тем точнее его середина будет характеризовать весь интервал. Далее используется обычная формула средней, только значения варианты будут приравниваться к середине соответствующего интервала. Расчет средней по непрерывному признаку (представленному в виде интервалов) был рассмотрен в примере 2.
В том случае, если ряд распределения имеет равные интервалы, расчет средней может быть существенно упрощен. Упрощенные способы расчета средней арифметической базируются на знании ее свойств.
Свойства средней арифметической:
- если все веса (f) увеличить или уменьшить в одинаковое число раз (d), то величина средней не изменится:
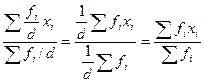
- если каждую варианту (х) увеличить или уменьшить на одну и ту же величину, то средняя увеличится или уменьшится на эту же величин:
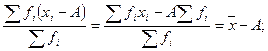
- если каждую варианту (х) увеличить или уменьшить в одно и то же число раз (h), то средняя увеличится или уменьшится в то же число раз.
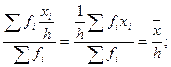
- сумма отклонений вариант от средней, взвешенных их частотами равна нулю:
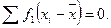
Перечисленные свойства средней арифметической используются при расчете средней способом моментов или способом отсчета от условного начала (0). При использовании этого способа последовательно осуществляются следующие операции:
— определяются срединные значения интервалов как полусумма начала и конца интервалов;
— варианта (серединное значение интервала) с наибольшей частотой принимается за условное начало отсчета (А);
— рассчитывается момент 1 -го порядка:
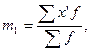
где 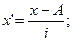
i — величина интервала.
Средняя рассчитывается по формуле:
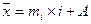
Пример расчета средней арифметической способом моментов.
Имеются следующие данные о продаже трехкомнатных квартир агентством недвижимости (табл. 6):
Таблица 6
| Стоимость квартир, тыс. руб. | Число квартир в группе, f | x | x’ | x’f |
| 250—300 | -2 | -300 | ||
| 300—350 | -1 | -200 | ||
| 350—400 | ||||
| 400—450 | ||||
| 450—500 | ||||
| 500—550 | 3 | |||
| 550—600 | 4 | |||
| 600—650 | ПО | |||
| Итого |
Определите среднюю стоимость квартиры.
При использовании способа моментов удобнее всего результаты расчетов заносить в таблицу, для этого заранее в таблице резервируется три расчетных графы.
На основании данных таблицы рассчитываем момент 1-го порядка: итог по 5 столбцу делим на итог по 2 столбцу.
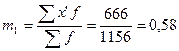
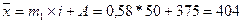 (тыс. руб.)
(тыс. руб.)
Средняя стоимость квартир выставленных на продажу составляет 404 тыс, руб.
Наряду со средней арифметической и средней гармонической, к другим степенным средним относится средняя геометрическая. В статистике она используется для осреднения темпов роста, коэффициентов динамики:
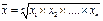
Средняя квадратическая используется при расчете показателей вариации, в частности — среднеквадратического отклонения, при исчислении средних ошибок выборки:
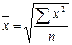 ,
, 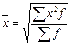
Дата добавления: 2016-12-16; просмотров: 1720;
