Структурные средние
Модаи медиана определяются структурой распределения. Они позволяют определить среднюю величину без производства вычислений, визуально. Их используют в том случае, когда расчет степенных средних невозможен или нецелесообразен.
В дискретном ряду распределения мода определяется визуально. Например, распределение семей по числу /детей:
1 ребенок 25
2 ребенка 30
3 ребенка 10
4 и более детей 2
В данном ряду распределения мода равна 2, то есть в данной совокупности наиболее часто встречаются семьи с двумя детьми. Очень удобно использовать этот показатель для характеристики наиболее часто встречаемого значения признака, определяемого по большой совокупности. Например, наиболее часто спрашиваемый размер обуви, размер одежды и т.д.
В интервальном ряду распределения, когда наиболее часто встречаемое значение признака задано в виде интервала, а мода должна отражать конкретное значение признака, используется следующая формула расчета:
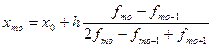
где xmo — мода;
х0 — верхняя граница модального интервала;
h — величина интервала:
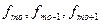 — частоты модального, предмодального и послемодальнего интервалов.
— частоты модального, предмодального и послемодальнего интервалов.
В качестве модального берется интервал с наибольшей частотой.
Пример расчета моды по интервальному ряду распределения. Имеются следующий ряд распределения по среднедушевому доходу населения (табл. 7):
Таблица 7
| Интервалы по среднедушевому доходу, руб. | Число семей, fi | Накопленные частоты, Si |
| До 100 | ||
| 100—150 | ||
| 150—200 | ||
| 200—250 | ||
| 250—300 | ||
| 300—350 | ||
| 350—400 | ||
| 450—500 | ||
| 550—600 | ||
| Итого | X |
По данным таблицы, наиболее часто встречаются семьи со среднедушевым доходом от 200 до 250, то есть наибольшей частоте (59) соответствует интервал 200—250. Данный интервал и будет модальным. Расчет по формуле позволяет получить более точное значение.
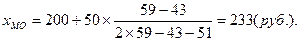
В данной совокупности наиболее часто встречаются семьи со среднедушевым доходом 233 рубля.
Медиана— варианта, которая делит ранжированный ряд распределения на две равные части. По обе стороны от медианы находится одинаковое число единиц совокупности.
В дискретном ряду распределения медиана определяется визуально. Ряд признаков ранжируется, то есть значения признака упорядочиваются по возрастанию или убыванию. Варианта, которая делит упорядоченный ряд пополам, будет медианой. Медиана в интервальном ряду распределения определяется по формуле:
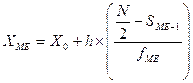
где XME — верхняя граница медианного интервала;
X0 — величина интервала;
h — общая численность;
Sме-1 — накопленные частоты предмедианного интервала:
fме — частота медианного интервала.
В качестве медианного берется интервал, в котором находится единица совокупности, которая делит упорядоченный по значению признака ряд пополам. Для того чтобы определить медианный интервал, рассчитывают накопленные частоты. Последняя накопленная частота показывает общее количество единиц совокупности.
Пример расчета медианы (по данным табл. 7). Последняя накопленная частота — 236. Медианный интервал должен содержать единицу совокупности, которая делит всю совокупность из 236 семей пополам (236/2 = 118). Значит, в качестве медианного в расчете будем брать интервал 200—250. так как среднедушевой доход до 200 руб. имеют 67 семей из данной совокупности, то есть менее половины совокупности. А интервалу 200—250 соответствует накопленная частота 126, значит, именно в этом интервале находится значение признака, которое разделит совокупность пополам, то есть 118 семей будут иметь среднедушевой доход ниже медианного и 118 семей — выше медианного. Произведем расчет медианы по формуле для интервального ряда:
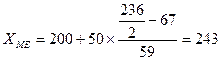
В изучаемой совокупности половина семей имеет доход ниже 243 руб. на человека.
Выводы:
1. Различают три вида статистических величин: абсолютные, относительные, средние величины.
2. Относительные величины позволяют приводить данные в сопоставимый вид и производить сравнения, в то время как абсолютные величины характеризуют только абсолютные размеры явления и в сравнительных характеристиках используются редко.
3. В статистической практике используют следующие виды относительных величин:
— планового задания;
— выполнения плана;
— динамики;
— координации;
— структуры;
— интенсивности;
— сравнения.
4. Наиболее распространены в статистических расчетах средние величины, которые могут одним числом охарактеризовать всю совокупность при соблюдении условий расчета средней величины.
5. Различают два класса средних величин: степенные и структурные.
6. При расчете степенных средних для правильного выбора формулы расчета необходимо исходить из логической формулы расчета осредняемого показателя.
Задание 1.4.1.Имеются следующие данные по магазинам ООО «Триумф»:
| Номер магазина | Процент выполнения плана | Товарооборот, тыс. руб. |
| № 1 №2 №3 |
Определите средний процент выполнения плана.
Задание 1.4.2.Имеются следующие данные по группе предприятий:
| № предприятия | Рентабельность, % | Реализованная продукция, тыс.руб. |
Определите среднюю рентабельность по группе предприятий.
Дата добавления: 2016-12-16; просмотров: 1030;
