Розрахунок плоских і просторових розмірних ланцюгів

Плоскі і просторові розмірні ланцюги розраховують тими ж методами, що і лінійні. Необхідно лише привести їх до виду лінійних розмірних ланцюгів. Це досягається шляхом проектування розмірів плоского ланцюга на один напрямок, що звичайно збігається з напрямком вихідного (чи замикаючого) розміру, а просторового ланцюга - на двох чи три взаємно перпендикулярні осі.

По формулах (2.12) і (2.18) визначимо допуск замикаючого розміру: методом розрахунку на максимум-мінімум

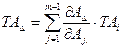; (2.22)

теорико-вірогідним методом

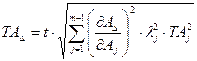. (2.23)

У відповідність з вираженням (2.10) одержимо рівняння замикаючого ланки 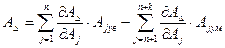. (2.24)

По аналоги з рівнянням (2.15) визначиться координата середини полючи допуску замикаючого ланки при зсуві її відносно середини полючи розсіювання при теоретико-вероятностном методі розрахунку: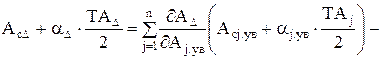

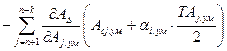. (2.25)

У рівняннях (2.22) – (2.25) дА_D!дА_j — приватна похідна функція замикаючого розміру по j-му складовому розміру; її називають також передатним відношенням .

Передатні відносини характеризують ступінь і характер впливу погрішностей розмірів складових ланок на замикаюче. Для ланцюгів з рівнобіжними ланками при розрахунку допусків усі передатні відносини дорівнюють одиниці (для розмірів, що збільшують,) чи мінус одиниці (для що зменшують).

Визначимо розмір А_D і допуск ТА_D замикаючого розміру плоского розмірного ланцюга, представленої на мал. 2.66.

дА_D!дА₁ = cosb; дА_D!дА₂ =1;

дА_D!дА₃ = cosg.

Номінальний розмір по формулі (2.24)

А_D = А₁ cosb +А₂ + А₃ cosg.

Допуск замикаючого розміру по формулі (2.22)

ТА_D = ТА₁ cosb + ТА₂ + ТА₃ cosg.

При розрахунку ланцюга теорико-вірогідний методом випливає скористатися залежностями (2.23) - (2.25).