Теоретико-вероятностный метод розрахунку розмірних ланцюгів

При розрахунку розмірних ланцюгів методом максимуму - мінімуму перед-покладалося, що в процесі чи обробки зборки можливо одночасне сполучення найбільших що збільшують і найменших уменьшающих розмірів чи зворотне їхнє сполучення. Обидва випадки найгірші в змісті одержання точності замикаючого ланки, але вони малоймовірні, тому що відхилення раз-меров в основному групуються біля середини полючи допуску. На цьому по-ложении і заснований теоретико-вероятностный метод розрахунку розмірних ланцюгів.

Застосування теорії імовірностей дозволяє розширити допуски со-ставляющих розмірів і тим самим полегшити виготовлення деталей при прак-тически незначному ризику недотримання граничних значень замикаючого розміру.

Зворотна задача. У результаті спільного впливу систематичних і випадкових погрішностей центр групування може не збігатися із серединою полючи допуску, а зона розсіювання - з величиною допуску. Величина такої розбіжності, виражена в часткахполовини допуску на розмір, називається коефіцієнтом асиметрії, ,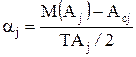

де М(А_i) – математичне чекання, середній арифметичний розмір i – го ланки;A_сi – розмір, що відповідає середині полючи допуску.

У цьому випадку рівняння розмірного ланцюга по середніх розмірах буде мати вид

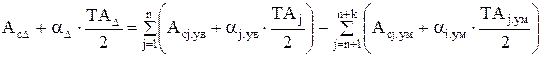. (2.15)

Використовуючи теорему про дисперсію [D(x_i) =s_i²] суммы независимых случайных величин, можно записать: 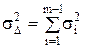. (2.16)

Для переходу від середніх квадратических відхилень s до чи допусків полям розсіювання використовують коефіцієнти відносного розсіювання l_i. Він є відносним середньої квадратическим відхиленням і дорівнює (при полі розсіювання w_j = T_j)

l_j = 2s_j/T_j . (2.17)

Для закону нормального розподілу (при T_j = 6s_j ) ;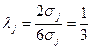

для закону рівної імовірності (при ) ;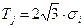

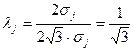для закону трикутника (Симпсона) (при ) .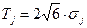

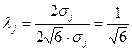Підставивши вираження (2.17) у рівняння (2.16), одержимо:

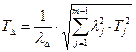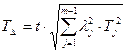чи , (2.18)

де t – коефіцієнт, що залежить від відсотка ризику і приймав за даними [10].

Визначивши ТА_D по формулі (2.18), обчислюють середнє відхилення замикаючого ланки як Е_с(А_D) = 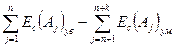(2.19)

і його граничні відхилення

Еs(А_D) = Е_с(А_D) + TA_D/2; Еi(А_D) = Е_с(А_D) - TA_D/2. (2.20)

Пряма задача. Допуски складових розмірів ланцюга при заданому допуску вихідного розміру можна розраховувати чотирма способами.

При способі рівних допусків приймають, що величини ТА_j, E_c(A_j) и l_j для всіх складових розмірів однакові. По заданому допуску TA_D по формулі (2.18) визначають середні допуски T_cA_j:

.

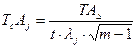Знайдені значення T_cA_j и E_c(A_j) коректують, з огляду на вимоги конструкції і можливість застосування процесів виготовлення деталей, економічна точність яких близька до необхідної точності розмірів. Правильність рішення задачі перевіряють по формулі (2.18).

При способі призначення допусків одного квалитета розрахунок у загальному аналогічний рішенню прямої задачі методом повної взаємозамінності. При цьому середня кількість одиниць допуску визначиться по формулі

.

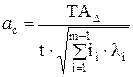Спосіб спробних розрахунків [50] полягає в тім, що допуски на складові розміри призначають економічно доцільними для умов майбутнього виду виробництва з урахуванням конструктивних вимог, досвіду експлуатації наявних подібних механізмів і перевірених для даного виробництва значень коефіцієнтів l. Правильність розрахунку перевіряють по формулі (2.18).

Спосіб рівного впливу [50]застосовують при рішенні плоских і просторових розмірних ланцюгів. Він заснований на тім, що відхилення кожного складового, що допускається, розміру повинне викликати однакова зміна вихідного розміру.
Приклад 2.Розрахувати допуски і граничні відхилення для розмірів А₁, А₃, А₄

І А₆ (см. мал. 2.64) при заданому А_D = 1…2,12 мм. ТА_D = 1,12 мм.

Скористаємося способом одного квалитета. Розрахунок ведеться в тієї ж последователь-ности, що й у прикладі 1.

Визначаємо коефіцієнт квалитета як

; ,

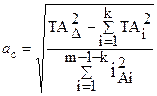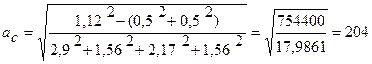де i_Ai прийняли по табл.3.3 [10]; k - кількість ланок із заданими допусками.

За ДСТ 25347 - 82* визначаємо, що значення а_С, рівне 204, знаходиться між по IT12 = 160 и IT13 = 250. По цьому ж стандарті визначаємо допуски на всі розміри по IT12: ТА₁ = 0,460; TA₃ = 0,250; TA₄ = 0,350; TA₆ = 0,250.

Визначаємо допуск замикаючого ланки по рівнянню(2.18): ,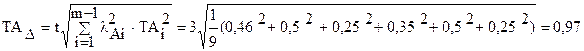

де l_Аi = 1/3 - коефіцієнт відносного розсіювання розмірів для нормального закону розподілу; t = 3 - коефіцієнт, що характеризує відсоток виходу розрахункових відхилень за межі допуску, задається в залежності від відсотка ризику (Р = 0,27%) [10].

Умова не виконана, тобто.. 1,12 ¹ 0,97.

Щоб одержати рівність допусків, допуск одного з ланок варто збільшити. Для цього вибираємо ланка А₁ (корпус) і визначаємо його допуск:

.

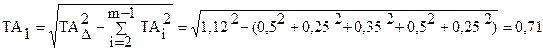Призначаємо відхилення складових ланок аналогічно попередньому прикладу:

A₁ = 240 ± 0,355; A₂ = 25_-0,5; A₃ = 50_-0,25; A₄ = 107_-0,35; A₅ = 21_-0,5; A₆ = 40 ± 0,125.

Визначаємо координати центрів групування розмірів, прийнявши коефіцієнт асиметрії a_i рівним нулю. Це означає, що розсіювання всіх складових ланок симетрично щодо середини полючи допуску, і координати центрів групування розмірів будуть відповідати координатам середин полів допусків

: Е_СА₁ = 0; E_CA₂ = -0,25; E_CA₃ = -0,125; E_CA₄ = -0,175; E_CA₅ = -0,25; E_CA₆ = 0.

Визначаємо відхилення і координати середини полючи допуску замикаючого ланки:

E_SA_D = A_Dmax - A_D = 2,12 – 3 = - 0,88; _iA_D = A_Dmin - A_D = 1,0 – 3 = -2,0;

E_CA_D =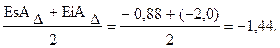

Перевіряємо координати середин полів допусків по рівнянню (2.19):

-1,44 ¹ [(-0,25) + (-0,125) + (-0,175) + (-0,25) + 0] – 0 = -0,8.

Для забезпечення рівності коректуємо координату середини полючи допуску ланки А₁: E_CA₁ = -0,8 – (-1,44) = +0,64.

Визначаємо відхилення ланки А₁:EsA₁ = E_CA₁ + ТА₁/2 = +0,64 + 0,71/2 = +0,995;

EiA₁ = E_CA₁ - ТА₁/2 = +0,64 - ,71/2 = +0,285. Звено А₁ = 240 .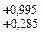

Перевірка. Тому що рівності в рівняннях (2.18) і (2.19) витримані, перевіряємо пре-дельные відхилення замикаючого ланкиА_D по формулах (2.20):

ЕsA_D = -1,44 + 1,12/2 = - 0,88; EiA_D = -1,44 - 1,12/2 = -2,0.

Вимоги по замикаючому ланці витримані.