Повну взаємозамінність

Щоб забезпечити повну взаємозамінність, розмірні ланцюги рас-зчитують методом максимуму-мінімуму, при який допуск замикаючого розміру визначають арифметичним додаванням допусків складових розмірів. Метод розрахунку на максимум-мінімум, що враховує тільки граничні відхилення ланок розмірного ланцюга і самі несприятливі їхні сполучення, забезпечує задану точність зборки без припасування (підбора) деталей.

Зворотна задача. Для висновку рівнянь розміру, граничних розмірів, граничних відхилень і допуску замикаючого ланки скористаємося прикладом лінійного розмірного ланцюга, приведеної на мал. 2.63.

Шукані значення для замикаючого ланки визначаться вираженнями: розмір А_D = А₁ – А₂; (2.6)

граничні розміри А_D^max = A₁^max – A₂^min , А_D^min = A₁^min – A₂^max; (2.7)

граничні відхилення Еs(A_D) = Es(A₁) – Ei(A₂), Еi(A_D) = Ei(A₁)–Es(A₂); (2.8)

допуск ТА_D = ТА₁ + ТА₂. (2.9)

За аналогією з рівняннями (2.6) - (2.9) за-висимости для замикаючого ланки при лінійному розмірному ланцюзі можна представити в загальному ви-ді:

розмір 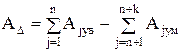; (2.10)

;

;

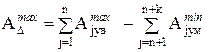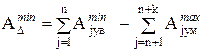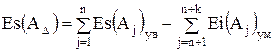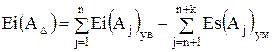Допуск 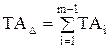, (2.12)

де n – кількість ланок, що збільшують; k – кількість ланок, що зменшують; m - загальна кількість звеньв, включаючи замикаюче ланку; Es - верхнє відхилення ланки; Eі - нижнє відхилення ланки.

Пряма задача. Така задача зустрічається на практиці частіше. Після визначення розмірів складових ланок у результаті конструювання механізму необхідно розрахувати допуски на ці розміри при заданій точності зборки (заданому допуску вихідного розміру). Точність складових розмірів повинна бути такий, щоб гарантувалася задана точність вихідного (функціонального) розміру. Цю задачу можна вирішувати одним з розглянутих далі способів.

Спосіб рівних допусків застосовують, якщо складові розміри мають один порядок (наприклад, входять в один інтервал діаметрів) і можуть бути виконані з приблизно однаковою економічною точністю. У цьому випадку з формули (2.12) одержимо середній допуск на ланку

Т_сА_i = TA_D/(m-1).

Цей допуск коректують для деяких складових розмірів у залежності від їхніх значень, конструктивних вимог і технологічних можливостей виготовлення, але так, щоб виконувалися умови по рівнянням (2.11) і (2.12). При цьому вибирають стандартні полючи допусків, бажано кращого застосування.

Спосіб рівних допусків простий, але недостатньо точний, тому що кор ректировка допусків складових розмірів довільна. Його можна рекомендувати тільки для попереднього призначення допусків складових розмірів.

Спосіб допусків одного квалитета застосовують, якщо всі складові ланцюг розміри можуть бути виконані з допуском одного квалитета і допуски складових розмірів залежать від їхнього номінального значення.

Необхідний квалитет визначають у такий спосіб.

Допуск складового розміру

ТА_i = а_i×i_i , (2.13)

де i — одиниця допуску (мкм); а — число одиниць допуску, що міститься в допуску даного розміру (визначається за ДСТ 25346 - 89).

Для розмірів від 1 до 500 мм 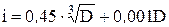, де D — середній геометричний розмір (мм) для інтервалу діаметрів за ДСТ 25346 - 89, до якого відноситься даний лінійний розмір.

Підставивши вираження (2.13) у рівняння (2.12) і вирішивши його

оносительно а, одержимо: 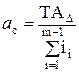. (2.14)

За значенням а_с вибирають найближчий квалитет. Число одиниць допуску а_с, обчислене по формулі (2.14), у загальному випадку не дорівнює

какомулибо значенню а, визначальному квалитет, тому вибирають найближчий квалитет. Знайшовши за ДСТ 25346 - 92 чи за ДСТ 25347 - 82* допуски складових розмірів, коректують їхнього значення, з огляду на конструктивно-експлуатаційні вимоги і можливість застосування процесу виготовлення, економічна точність якого близька до необхідної точності розмірів. Допуски для розмірів, що охоплюють, рекомендується визначати, як для основного отвору, а для охоплюваних - як для основного вала. При цьому варто задовольнити рівнянню (2.12).

Знайшовши допуски, визначають значення і знаки верхніх і нижніх відхилень складових розмірів так, щоб вони задовольняли рівнянням (2.11).

Рішення прямої задачі способом призначення допусків одного квалите-та більш обґрунтоване, чим рішення способом рівних допусків.

Приклад 1.Розрахувати допуски і граничні відхилення для розмірів А₁, А₃, А₄

і А₆ (мал. 2.64) при заданому А_D = 1…3,5 мм.

Вирішимо цю задачу методом повної взаємозамінності способом одного квалитета.

Відповідно до рівняння розмірного ланцюга (2.10) A_D = A₂ + A₃ + A₄ + A₅ + A₆ - A₁ = (25 + 50 + 107 + 21 + 40) – 240 = 3.

Визначаємо число одиниць чи допуску коефіцієнт квалитета. Для цього використовуємо рівняння (2.14): ,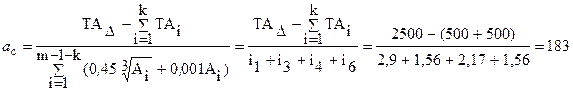

де i_Ai прийняли по табл.3.3 [10]; k - кількість ланок із заданими допусками.

Знаючи число одиниць допуску а_с, за ДСТ 25347 - 82* визначаємо номер квалитета. У розглянутому випадку значення знаходиться між IТ12 (а= 160) і IТ13 (а = 250).

Рекомендується вибирати допуски по більш грубому квалитету. Однак у нашому слу-чае а_с ближче до ІТ12, тому допуски на розмір корпуса А₁ установлюємо по IТ13, а на інші (більш технологичные у виготовленні розміри) - по IТ12.

Виходячи з номінальних розмірів ланок ланцюга й обраних квалитетов, за ДСТ 25347-82* визначаємо допуски складових ланок:ТА₁ = 720 мкм; ТА₃ = 250 мкм; ТА₄ = 350 мкм; ТА₆ = 250 мкм.

Зробимо перевірку суми встановлених допусків складових ланок з залишком допуску замикаючого ланки, що повинний розподілитися на що залишилися складові ланки: 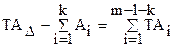. 1500 ¹ 720 + 250 + 350 + 250 = 1570.

Коректуємо допуск однієї складового ланки так, щоб вийшла рівність допусків. Тому що необхідно зменшити допуск одного з ланок, по конструкції вузла варто проаналізувати, який розмір економічно вигідніше виконати більш точним. Приймаємо, що найбільше технологичны розміри А₃ і А₄.

Вибираємо для коректування розмір А₄ і зменшуємо допуск на його виготовлення на 70 мкм: ТА₄ = 280 мкм. У цьому випадку рівність допусків дотримана.

Призначаємо відхилення для всіх складових ланок.

У розглянутому прикладі на всі розміри призначаємо відхилення в мінус, за ис-ключением розмірів А₁ і А₆, для який відхилення призначаємо симетрично.

Проставляємо відхилення на розміри: A₁ = 240 ± 0,360; A₂ = 50 _{- 0,250};

A₄ = 107_{- 0,280}; A₆ = 40 ± 0,125.

Робимо перевірку відхилень складових ланок по відхиленнях замикаючої ланки: E_SA_D= A_Dmax - A_D = 3,5 – 3 = + 0,5; E_iA_D = A_Dmin - A_D = 1 – 3 = -2,0;

.

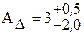Перевіряємо відповідність відхилень по рівняннях (2.11):

+0,5 = (0 + 0 + 0 + 0 + 0,125) – (-0,360) = 0,125 + 0,360.

Поставлена умова не задовольняється. Тоді приймаємо невідомими відхилення для тієї ланки, у якого коректували допуск (нестандартний допуск), тобто .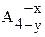

Це ланка що збільшує, значить з рівняння (2.11) визначається його верхнє от-клонение: + 0,5 – 0,125 – 0,360 = x; x = + 0,015.

Знаючи верхнє відхилення і допуск, визначимо нижнє відхилення по формулі

ei = + es – T; відкіля y = 0,015 – 0,280 = -0,265; .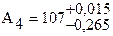

Перевіримо друге відхилення по формулі (2.11):

-2,0 = (-0,250) + (-0,5)×2 + (-0,265)+ (-0,125) – (+0,360) = - 2,0.

Рівність задовольняється, значить усі допуски і відхилення складових ланок визначені правильно.