Изображение плоских фигур в параллельной проекции

Пусть - плоскость изображения;

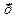- вектор проектирования;

F- оригинал;

F₀ – проекция F;

F₁–подобна F₀

F₁ – изображение F.

Любую фигуру F₁ на плоскости , подобную фигуре F₀ ,

называют изображением фигуры F

Теорема 10.3. Пусть фигуры F и F’ лежат соответственно на пересекающих плоскостях и 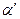. Фигура F может служить изображением фигуры F’ тогда и только, когда фигуры F и F’ аффинно - эквивалентны, то есть существует аффинное преобразование f: ’→ , которое F’→ F .

Доказательство.

1. Пусть фигура F плоскости является изображением фигуры F’ плоскости ’. Докажем, что фигуры аффинно-эквивалентны. Рассмотрим проекцию 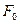фигуры F’. Так как параллельное проектирование является аффинным отображением, то фигуры аффинно-эквивалентны. С другой стороны, фигуры F и F’ подобны, а значит и аффинно-эквивалентны.

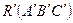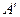2. Допустим теперь, что фигура F’ плоскости ’ аффинно-эквивалентна фигуре F плоскости . Докажем, что F можно рассматривать как изображение F’. Так как фигуры аффинно-эквивалентны, то существует аффинное отображение f, переводящее F’→ F. Выберем репер плоскости ’ так, чтобы точки и 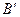лежали на линии пересечения плоскостей и ’, рассмотрим образ данного репера 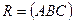при аффинном отображении .

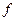На плоскости построим точку С₀ так, чтобы треугольники 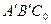и АВС были подобны. Параллельное проектирование 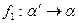по направлению вектора 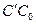переводит репер 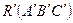в репер 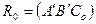. Рассмотрим подобие 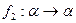, при котором репер 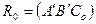переходит в репер 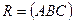. Очевидно, композиция 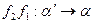есть аффинное отображение, переводящее 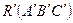в 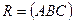и поэтому совпадает с отображением f. Таким образом, 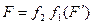. Но 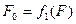- параллельная проекция фигуры F’ на плоскость , поэтому 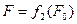- изображение фигуры F’.

1) Треугольник. Любой треугольник А₁В₁С₁ может служить изображением ∆АВС принадлежащего плоскости , так как можно задать аффинное отображение переводящее ∆ А₁В₁С₁ с учетом того что и ’ пересекаются. Если ‌‌ ’ то ∆ А₁В₁С₁ и ∆АВС должны быть подобными.

2) 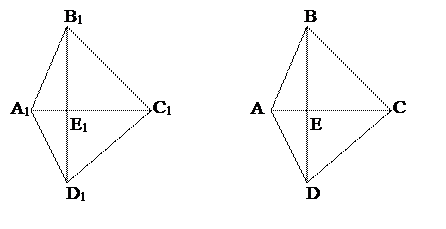Четыреугольник. Любой четырехугольник А₁В₁С₁D_{1 ,} является изображением четырехугольника А₁В₁С₁D₁ тогда и только тогда, когда четырехугольники А₁В₁С₁D₁ и АВСD является аффинно-эквивалентными (А₁В₁С₁D₁ и АВСD, если их обозначили таким образом, что (АС,Е)=(А₁С_1,Е₁), (BD,E)= (B₁D₁,E₁)). Для построения изображения АВСD четырехугольника А₁В₁С₁D₁ в качестве вершин А, В, С можно выбрать три произвольные точки, не лежащие на одной прямой. Положение четвертой вершины D определяется однозначно из условий: (АС,Е)=(А₁С_1,Е₁) , (BD,E)= (B₁D₁,E₁)).

3) Трапеция.Изображением трапеции является трапеция, у которой сохраняется отношение основания (параллельность)

4) Параллелограмм (ромб, прямоугольник, квадрат) Изображение есть параллелограмм. Любой параллелограмм является изображением квадрата и прямоугольника.

5) n- угольник (n>4) три вершины изображаются берутся произвольно, а остальные находятся построением, учитывая простое отношение трех точек.

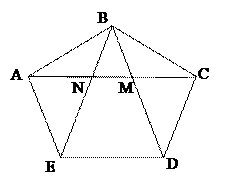
Изображая правильный шестиугольник, удобнее брать произвольно две вершины и центр. Остальные вершины строят, пользуясь симметричностью и параллельностью сторон.

6) Окружность.Построение окружности основано на следующей лемме.

Лемма 10.4. В любом аффинном отображении эллипс (в частности окружность) переходит в эллипс.

Из леммы и предыдущей теоремы следует, что изображением окружности является эллипс. При этом изображением центра окружности является центр эллипса, а изображением взаимно перпендикулярных диаметров - сопряженные диаметры эллипса.