Изображение многогранников в параллельной проекции.

Лемма 10.5. Пусть четырехугольник А₁В₁С₁D₁ и АВСD, лежащие соответственно в плоскостях 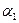и аффинно-эквивалентны. Тогда существует такая плоскость 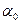,что проекция четырехугольника А₁В₁С₁D₁ на эту плоскость по направлению вектора, ортогонального к плоскости 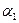, подобна четырехугольнику АВСD.

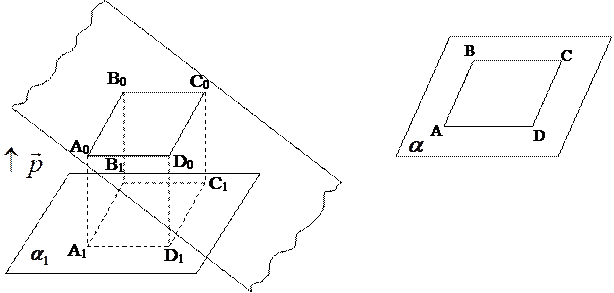
Теорема 10.6 (Польке- Шварца) Вершины любого четырехугольника АВСD плоскости , заданные в определенном порядке, могут служить изображением аффинного репера, равного данному реперу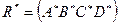

Доказательство

1). На прямых А*С* и B*D* возьмем соответственно М* и N*: (А*С*,М*)=(АС,Е), (В*D*,N*)=(BD,E).

2). Пусть 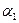перпендикулярна М*N* . Рассмотрим ортогональную проекцию А₁В₁С₁ D₁ репера 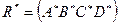. Точки М* и N* проектируются в одну и ту же точку 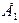.Так как (А₁С_1,Е₁)=(А*С*,М*)=(АС,Е), и (B,D,E)= (B*D*,N*)=(BD,E), то А₁В₁С₁D₁ и АВСD - аффинно-эквивалентны.

3). По предыдущей лемме существует такая плоскость 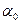, проекция А₀В₀С₀D_0- четырехугольника А₁В₁С₁D₁ на эту плоскость по направлению вектора М*N* подобна четырехугольника АВСD.

4). А₀ – параллельная проекция точки А* на плоскость 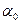по направлению вектора М*N*. Аналогично точки В_0, С_0, D₀ - параллельные проекции точек В*, С*,D* на эту же плоскость, а значит А₀В₀С₀D₀ – параллельная проекции репера 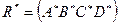на плоскость .

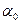5). Рассмотрим движение 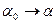, А₀В₀С₀D₀→ АВСD_, значит АВСD - изображение репера .

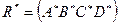а) Тетраэдр- изображение есть фигура, состоящая из всех сторон и диагоналей четырехугольника АВСD. Из теоремы: Вершины произвольного четырехугольника плоскости могут служить изображением вершин тетраэдра, равного данному.

б) Параллелепипед - изображение есть фигура, состоящая из трех пар параллелограммов, причем в каждой паре один получается из другого параллельным переносом. С учетом теоремы в качестве изображений вершин А,В,С,D можно выбрать вершины произвольного четырехугольника А,В,С,D некоторой плоскости, остальные же вершины изображаются построением с учетом того, что грани параллелепипеда – параллелограммы.

в) Призма(n- угольная) – фигура, состоящая из двух равных n- угольников, (один из которых получается параллельным переносом из другого), изображающих основания призмы, и n-параллелограммов, для каждого из которых противоположными сторонами являются изображения параллельных сторон оснований.

г) Пирамида- фигура, состоящая из многоугольника, изображающего основание пирамиды-оригинала, и несколько треугольников с общей вершиной, изображающих боковые грани. Для построения пирамиды по теореме Польке-Шварца за изображение вершины пирамиды и трех вершин оснований можно взять вершины произвольного четырехугольника некоторой плоскости. Тогда изображения остальных вершин основания получаются построением с учетом правил построения изображений плоских многоугольников.