Свойства параллельного проектирования.
Параллельное проектирование. Аффинные отображения.
Изображение плоских фигур в параллельной проекции.
Изображение многогранников в параллельной проекции.


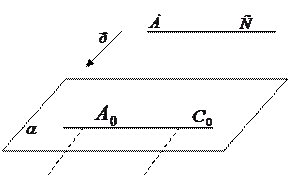 Пусть дана плоскость
Пусть дана плоскость  точка
точка 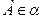 и
и  .
.
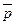 -вектор проектирования,
-вектор проектирования, 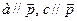
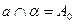
|
|
 при проектировании параллельно
при проектировании параллельно 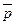
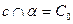 - проекция точки С на плоскость
- проекция точки С на плоскость  при проектировании параллельно вектору
при проектировании параллельно вектору  .
.
 - проективная плоскость,
- проективная плоскость, 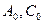 - параллельные проекции точек
- параллельные проекции точек  ,
,
 - основная плоскость изображения. Если
- основная плоскость изображения. Если  ┴
┴  , то
, то 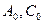 – ортогональные проекции.
– ортогональные проекции.
Свойства параллельного проектирования.
1)Проекция прямой есть прямая.
2)Проекции параллельных прямых параллельны или совпадают;
3)Проекция отрезка АВ - есть отрезок, концами которого является проекции точек А и В;
4)При параллельном проектировании сохраняется простое отношение трех точек; в частности, проекция середины отрезка есть середина проекции отрезка;
5)Проекции параллельных отрезков либо параллельна, либо находится на одной прямой;
6)Проекции параллельных отрезков или отрезков, лежащих на одной прямой, пропорциональны самим отрезкам.
Определение 10.1. Аффинным отображением f: α→α’ называется взаимно однозначное отображение, которое переводит три точки, лежащие на одной прямой плоскости  , в три точки, лежащие на одной прямой плоскости
, в три точки, лежащие на одной прямой плоскости 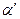 и сохраняет простое отношение трех точек.
и сохраняет простое отношение трех точек.
Определение 10.2. Аффинное отображение 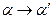 является параллельным проектированием
является параллельным проектированием  на
на 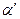 , если указано направление проектирования (вектора
, если указано направление проектирования (вектора 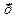 ) и если точка М, принадлежащая
) и если точка М, принадлежащая  переходит в точку М’
переходит в точку М’ 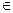 α’ и
α’ и  .
.
При аффинном отображении одной плоскости на другую прямая переходит в прямую, параллельные прямые – в параллельные прямые, полуплоскость – в полуплоскость, луч – в луч, отрезок – в отрезок, угол – в угол, репер – в репер, выпуклый (невыпуклый) многоугольник переходит в одноименный выпуклый (невыпуклый) многоугольник.
Дата добавления: 2017-01-29; просмотров: 1951;


