Вычисление площадей плоских фигур
 у
у
+ +
0 a - b
x
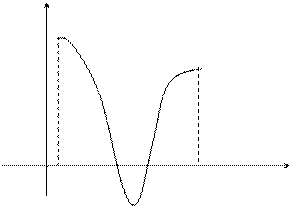
Определенный интеграл от неотрицательной функции 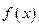 на отрезке
на отрезке 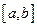 представляет собой площадь криволинейной трапеции, ограниченной графиком функции
представляет собой площадь криволинейной трапеции, ограниченной графиком функции 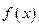 , отрезком
, отрезком 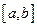 и отрезками прямых
и отрезками прямых 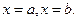 Если график функции
Если график функции 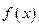 расположен ниже оси Ох, т.е.
расположен ниже оси Ох, т.е. 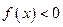 , то интеграл берётся со знаком “-“, если график расположен выше оси Ох, т.е.
, то интеграл берётся со знаком “-“, если график расположен выше оси Ох, т.е. 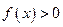 , то интеграл берётся со знаком “+”.
, то интеграл берётся со знаком “+”.
Для нахождения суммарной площади используется формула 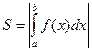 .
.
Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.
Пример. Найти площадь фигуры, ограниченной линиями 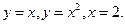
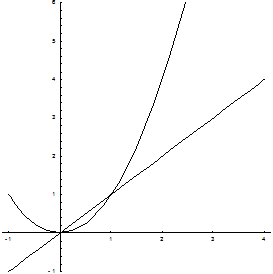
Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
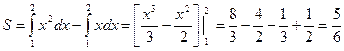 (ед2)
(ед2)
Нахождение площади криволинейного сектора.
 |
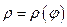
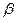
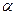
О 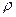
Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид 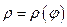 , где
, где 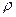 - длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а
- длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а 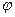 - угол наклона этого радиус – вектора к полярной оси.
- угол наклона этого радиус – вектора к полярной оси.
Площадь криволинейного сектора находится по формуле:
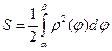 .
.
Дата добавления: 2016-05-05; просмотров: 710;
