Понятие несобственного интеграла
Пусть функция 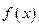 определена и непрерывна на интервале
определена и непрерывна на интервале 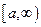 . Тогда она непрерывна и, следовательно, интегрируема на любом конечном отрезке
. Тогда она непрерывна и, следовательно, интегрируема на любом конечном отрезке 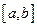 .
.
Определение. Предел 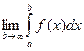 называется несобственным интегралом от функции
называется несобственным интегралом от функции 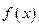 на интервале
на интервале 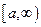 .
.
Обозначение: 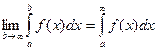
Определение.Если этот предел существует и конечен, то говорят, что несобственный интеграл называется сходящимся. Если предел не существует или бесконечен, то несобственный интеграл называется расходящимся.
Аналогичные рассуждения можно привести для несобственных интегралов вида:
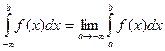 ,
, 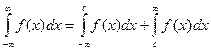
при условии, если входящие в них интегралы существуют.
Пример.
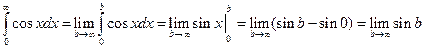 - не существует.
- не существует.
Несобственный интеграл расходится.
Пример.
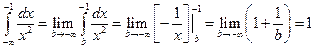 - интеграл сходится
- интеграл сходится
Несобственные интегралы от неотрицательных функций
Теорема. Если для всех 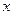
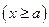 выполняется условие
выполняется условие 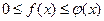 и интеграл
и интеграл 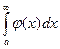 сходится, то
сходится, то 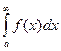 тоже сходится и
тоже сходится и 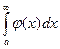 ³
³ 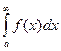 .
.
Теорема. Если для всех 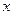
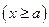 выполняется условие
выполняется условие 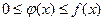 и интеграл
и интеграл 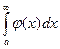 расходится, то
расходится, то 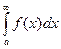 тоже расходится.
тоже расходится.
Теорема. Если 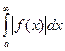 сходится, то сходится и интеграл
сходится, то сходится и интеграл 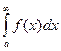 .
.
В этом случае интеграл 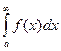 называется абсолютно сходящимся.
называется абсолютно сходящимся.
Дата добавления: 2016-05-05; просмотров: 790;
