Тема 6. Средние величины

Статистическая совокупность содержит некоторое количество статистических величин, имеющих, как правило, разные значения и признаки, что делает невозможным сравнение нескольких совокупностей в целом. Для этой цели применяется средняя величина, как обобщающий показатель совокупности, характеризующий уровень изучаемого явления или процесса.То есть она отражает то общее, что присуще всем единицам совокупности. Сущность средней заключается в том, что в ней взаимопогашаются те отклонения значений признака, которые обусловлены случайными факторами и учитываются изменения, вызванные основными факторами.

Расчет большинства средних статистических показателей основан на использовании средней агрегатной, средней арифметической и средней гармонической.

Средняя агрегатная

где W_i=x_i*f_i , x_i -i-тый вариант осредняемого признака, f_i – вес i-того признака.

Средняя арифметическая взвешенная

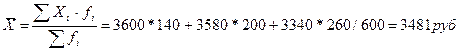
Средняя арифметическая невзвешенная

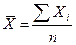, где n – объем совокупности.

Эта средняя исчисляется, когда веса f отсутствуют (каждый вариант встречается один раз).

среднюю заработную плату по трем предприятиям произведем по средней гармонической.

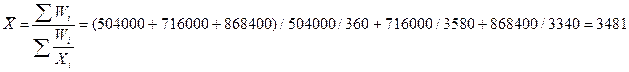
При равенстве весов (W) расчет средней производится по средней гармонической невзвешенной.

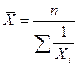
Средняя арифметическая и средняя гармоническая получили широкое применение в плановых расчетах при расчете общей средней из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок .Средние показатели могут рассчитываться по дискретным (прерывным) и интервальным (непрерывным) вариационным рядам. Для дискретного ряда средние рассчитываются как для вышеприведенного примера. В интервальном ряду для расчета определяется середина интервала.

Виды средних

4. Средняя геометрическая:

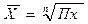
5. Средняя степенная:

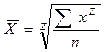
Средняя квадратическая:

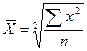
Средняя кубическая:

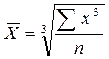
Средняя квадратическая применяется для расчета среднего квадратического отклонения, являющегося показателем вариации признаков. Средняя геометрическая используется при вычислении среднего коэффициента роста в рядах динамики.