Уравнения плоского движения твердого тела
В декартовой системе координат:
Пусть под действием системы внешних сил 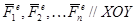 тело совершает плоское движение
тело совершает плоское движение
Из кинематики известно, что плоское движение твердого тела можно рассматривать как поступательное движение полюса (например, центра масс тела) и вращение тела вокруг него.
 Поступательная часть движения определяется теоремой о движении центра масс системы:
Поступательная часть движения определяется теоремой о движении центра масс системы:
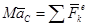 , причем
, причем 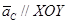
Вращательное движение тела вокруг центра масс определяется уравнением вращательного движения:
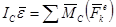 , причем
, причем 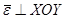 .
.
Спроецировав эти векторные уравнения на оси декартовых координат, получим три дифференциальных уравнения плоского движения тела:
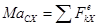 ;
;
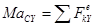 ;
;
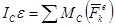
 В естественных координатах:
В естественных координатах:
Вектор ускорения 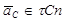 (лежит в соприкасающейся плоскости), а вектор углового ускорения
(лежит в соприкасающейся плоскости), а вектор углового ускорения 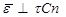 ,
, 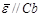 . Уравнения плоского движения тела в проекциях на оси естественного трехгранника
. Уравнения плоского движения тела в проекциях на оси естественного трехгранника 
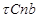 :
:
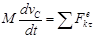 ;
;
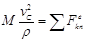 ;
;
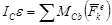 .
.
Вопросы для самоконтроля
Ø Что такое количество движения точки, системы? В каких единицах измеряется эта величина?
Ø Сформулируйте теоремы об изменении количества движения точки, системы.
Ø Сформулируйте закон сохранения количества движения системы.
Ø Что такое момент количества движения точки, системы? В каких единицах измеряется эта величина?
Ø Сформулируйте закон сохранения кинетического момента системы.
Ø Какую часть движения системы характеризуют количество движения, кинетический момент относительно оси?
Ø Запишите уравнение вращательного движения твердого тела.
Ø Запишите формулы для определения периода колебаний физического и математического маятника.
Ø Как экспериментально определить радиус инерции твердого тела?
Ø Запишите уравнения плоского движения твердого тела в декартовых и естественных системах координат.
ЛЕКЦИЯ №15
Принцип Даламбера
На принципе Даламбера основан метод кинетостатики, с помощью которого уравнениям движения по форме придается вид уравнений статики.
15.1.1 Принцип Даламбера для материальной точки: Если в любой момент времени к действующим на точку активным силам и реакциям связей присоединить силу инерции, то полученная система сил будет уравновешенной.
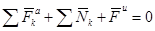 .
.
В проекциях на оси декартовых координат:
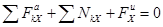 ;
;
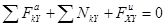 ;
;
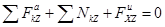 .
.
В естественных координатах силу инерции раскладывают на нормальную и касательную составляющие:
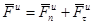 ,
,
где 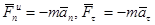
15.1.2 Принцип Даламбера для несвободной механической системы: В любой момент времени для всякой несвободной механической системы геометрическая сумма внешних сил, реакций связей и сил инерции равна нулю. Такая система является уравновешенной и к ней можно применить уравнения равновесия статики.
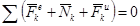 ;
;
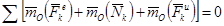 ,
,
где 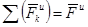 - главный вектор сил инерции;
- главный вектор сил инерции;
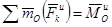 - главный момент сил инерции.
- главный момент сил инерции.
По теореме о движении центра масс главный вектор сил инерции равен:
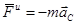 .
.
Главный вектор сил инерции механической системы равен произведению массы системы на ускорение центра масс системы и направлен противоположно этому ускорению.
Главный момент сил инерции равен:
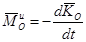 ;
; 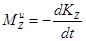
Главный момент сил инерции механической системы относительно некоторого центра О или оси Z равен взятой со знаком «-» производной по времени от кинетического момента относительно того же центра или той же оси.
Дата добавления: 2016-05-11; просмотров: 1079;
