Векторный способ задания движения точки
 Одной из важных характеристик движения точки является траектория ее движения, т.е. геометрическое место последовательных (с течением времени) положений точки в пространстве. Векторный способ используют для введения и исследования наиболее общих понятий кинематики и получения наиболее общих закономерностей.
Одной из важных характеристик движения точки является траектория ее движения, т.е. геометрическое место последовательных (с течением времени) положений точки в пространстве. Векторный способ используют для введения и исследования наиболее общих понятий кинематики и получения наиболее общих закономерностей.
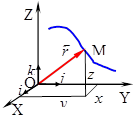
Закон движения точки М в векторной форме задается радиус-вектором, проведенным из точки О к точке М, как функции времени t.
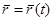 ,
,
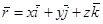 .
.
 Траекторией точки является годограф радиус-вектора.
Траекторией точки является годограф радиус-вектора.
Скорость – это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.
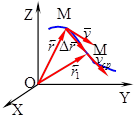
За время 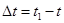 точка переместится по траектории из положения М в положение М1 определяемые радиусами векторами
точка переместится по траектории из положения М в положение М1 определяемые радиусами векторами 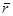 и
и 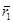 . Вектор перемещения
. Вектор перемещения 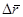 равен:
равен:
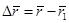 .
.
Средняя скорость точки М за этот промежуток равна:
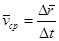 .
.
Вектор  зависит от промежутка времени
зависит от промежутка времени 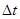 и направлен по хорде
и направлен по хорде 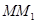 в сторону движения. Пусть
в сторону движения. Пусть  тогда:
тогда:
 .
.
 Вектор скорости
Вектор скорости 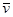 точки М в данный момент времени равен первой производной от радиуса-вектора
точки М в данный момент времени равен первой производной от радиуса-вектора 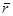 по времени t и направлен по касательной к траектории в сторону движения.
по времени t и направлен по касательной к траектории в сторону движения.  .
.
За промежуток времени 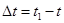 точка переместится из положения M в положение M1, и при этом ее скорость изменится от
точка переместится из положения M в положение M1, и при этом ее скорость изменится от 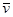 до
до 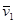 .
. 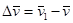 .
.
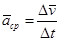 .
.
Причем вектор  и вектор
и вектор 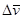 всегда направлен в сторону вогнутости траектории.
всегда направлен в сторону вогнутости траектории.
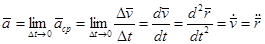 .
.
Ускорение точки 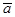 характеризует изменение вектора скорости
характеризует изменение вектора скорости 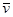 по величине и направлению с течением времени. Ускорение
по величине и направлению с течением времени. Ускорение 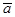 равно первой производной по времени от вектора скорости
равно первой производной по времени от вектора скорости 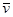 и второй производной от радиус-вектора точки М. Вектор
и второй производной от радиус-вектора точки М. Вектор 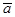 лежит в соприкасающейся плоскости и всегда направлен в сторону вогнутости траектории. Положение соприкасающейся плоскости определяется предельным положением плоскости проведенной через векторы
лежит в соприкасающейся плоскости и всегда направлен в сторону вогнутости траектории. Положение соприкасающейся плоскости определяется предельным положением плоскости проведенной через векторы 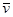 и
и 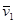 при стремлении точки М1 к точке М.
при стремлении точки М1 к точке М. 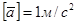 .
.
Дата добавления: 2016-05-11; просмотров: 801;
