Центр тяжести твердого тела
Если твердое тело находится вблизи поверхности Земли, то к каждой материальной точке этого тела приложена сила тяжести. При этом размеры тела по сравнению с размером Земли настолько малы, что силы земного притяжения, действующие на все частицы тела, можно считать параллельными между собой
Центр (точка С) системы параллельных сил тяжести  всех точек тела называется центром тяжести твердого тела, а сумма сил тяжести всех его материальных точек называется силой тяжести, действующей на него
всех точек тела называется центром тяжести твердого тела, а сумма сил тяжести всех его материальных точек называется силой тяжести, действующей на него
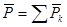 .
.
Координаты центра тяжести твердого тела определяются по формулам:

где  - координаты точек приложения сил тяжести
- координаты точек приложения сил тяжести  , действующих на k-ю материальную точку.
, действующих на k-ю материальную точку.
Для однородного тела:
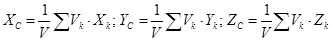 ,
,
где V - объем всего тела;
Vk - объем k-й частицы.
Для однородной тонкой пластины:
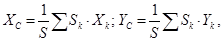
где S – площадь пластины;
Sk – площадь k-ой части пластины.
Для линии:
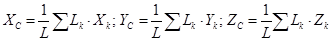 ,
,
где L - длина всей линии;
Lk - длина k-ой части линии.
Способы определения координат центров тяжести тел:
Теоретические
Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси, или в центре симметрии.
Разбиение. Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно непосредственно вычислить по выше приведенным формулам.
Дополнение. Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. В расчеты их включают со знаком «-».
Интегрирование. Когда тело нельзя разбить на составные части, центры тяжести которых известны, используют метод интегрирования, являющийся универсальным.
Экспериментальные
Метод подвешивания. Тело подвешивают за две-три точки, проводя из них вертикали. Точка их пересечении – центр масс.
Метод взвешивания. Тело разными частями помещают на весы, определяя тем самым опорные реакции. Составляют уравнения равновесия, из которых определяют координаты центра тяжести.
 С помощью теоретических методов выведены формулы для определения координат центра тяжести наиболее распространенных однородных тел:
С помощью теоретических методов выведены формулы для определения координат центра тяжести наиболее распространенных однородных тел:
Дуга окружности
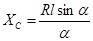
Дата добавления: 2016-05-11; просмотров: 1213;
