Координатный способ задания движения точки
При координатном способе закон движения точки (уравнения движения точки) в пространстве задается тремя координатами (декартовыми координатами) как функциями времени:
X = f1(t); Y = f2(t); Z = f3(t);
на плоскости – двумя координатами:
X = f1(t); Y = f2(t);
при прямолинейном движении – одной координатой:
 X = f1(t).
X = f1(t).
Для получения уравнения траектории точки из уравнений движения исключают время.
Так как 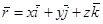 , то скорость точки равна:
, то скорость точки равна:
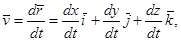 но
но
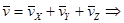
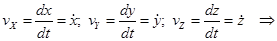
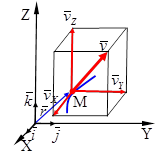
Проекции вектора скоростина оси декартовых координат равны первым производным от соответствующих координат по времени.
Модуль вектора скоростиравен
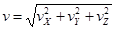 .
.
Вектор 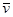 образует с осями координат углы, определяемые направляющими косинусами
образует с осями координат углы, определяемые направляющими косинусами
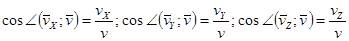 .
.
Ускорение точки равно:
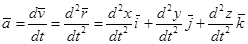 .
.
С другой стороны
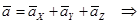
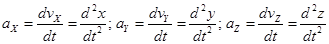
Проекции вектора ускорения на оси декартовых координат равны первым производным от проекций скорости или вторым производным от координат точки по времени.
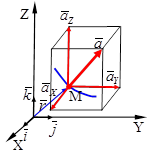 Модуль вектора ускорения равен:
Модуль вектора ускорения равен:
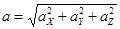 ;
;
Углы вектора ускорения с осями координат:
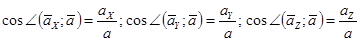 .
.
Дата добавления: 2016-05-11; просмотров: 720;
