Естественный способ задания движения точки
Для применения естественного способа задания движения точки должна быть известна ее траектория. Траектория может быть задана различными способами:
- уравнениями (возможно с неравенствами), например,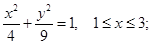 
- словесно, например, радиус окружности равен 3м;
- в виде графика в масштабе.
Для задания закона движения точки по известной траектории необходимо:
- 
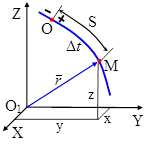выбрать на траектории начало отсчета расстояний – точку О и указать направление положительного отсчета (знак «+»);
- выбрать начало отсчета времени t =0, обычно за начало отсчета времени принимают или начало движения или момент времени, когда движущаяся точка М проходит через точку О.
Закон движения точки М по траектории имеет вид:
где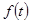 
- непрерывная дважды дифференцируемая функция, причем это выражение определяет положение точки на траектории, но не пройденный ею путь.
.
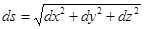Если при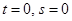 
, то
.
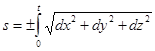Если известен закон движения точки в декартовых координатах, то
,
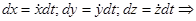
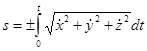где знак «+» или «–» определяется выбором положительного или отрицательного направления отсчета расстояний по траектории. Это выражение устанавливает связь естественного способа задания движения точки с координатным.
Скорость точки равна:
,
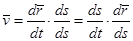Но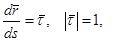 
единичный вектор 
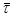направлен по касательной к траектории в сторону движения точки М, следовательно, скорость точки М направлена по касательной к траектории в сторону движения и равна
.
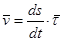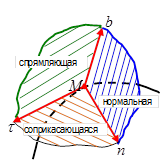
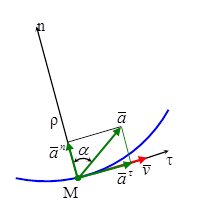
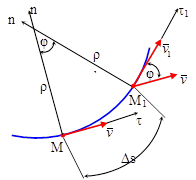Совместим с движущейся по траектории точкой М начало подвижной системы координат – оси естественного трехгранника Мtnb. Ось Mt - касательную направим по касательной к траектории в сторону движения точки. Ось Мn – главную нормаль направим перпендикулярно Мt в сторону вогнутости траектории так, чтобы эти оси образовали соприкасающуюся плоскость. Ось Мb- бинормаль направим перпендикулярно соприкасающейся плоскости в сторону, откуда поворот от оси Мt к оси Mn виден против хода часовой стрелки. Образовались еще две координатные плоскости: Mnb - нормальная и Mtb – спрямляющая.
Пусть точка М переместилась в положение М1. Векторы ее скорости в этих точках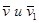 
образуют угол смежности φ.
,
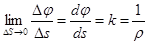k – кривизна кривой в точке М,
ρ – радиус кривизны кривой в точке М.
Ускорение точки М равно:
,
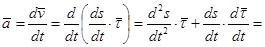
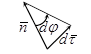
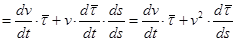но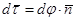 
, следовательно
.
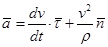Вектор ускорения точки М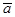 
разложен на две взаимно перпендикулярные составляющие лежащие в соприкасающейся плоскости:
- касательное (тангенциальное) ускорение, направленное по касательной к траектории, характеризующее изменение скорости по величине;
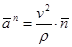- нормальное (центростремительное) ускорение, направленное перпендикулярно касательному в сторону вогнутости траектории, характеризующее изменение скорости по направлению.
Модуль ускорения равен:
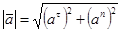
Направление ускорения по отношению к нормали определяется углом α:
.
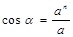Дата добавления: 2016-05-11; просмотров: 1043;