Угловая скорость тела не зависит от выбора начала координат или полюса.

.

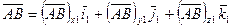
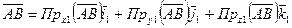В подвижном трехграннике проекции не изменяются.

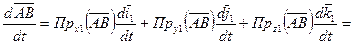
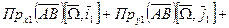
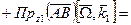
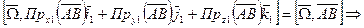
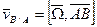
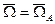, А- полюс. .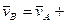

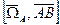Пусть С- произвольная точка АТТ.

.

.

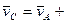
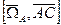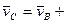
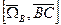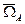- угловая скорость для точки А., 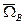- угловая скорость для точки В.

= = +

=

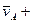
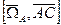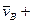
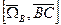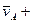
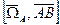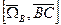
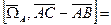
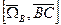
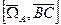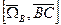
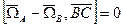
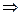
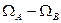
Таким образом, доказана теорема о независимости угловой скорости от выбора полюса.

Где бы ни находилось начало трехгранника, угловая скорость остается одной и той же.

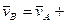
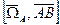- формула Эйлера для связи скоростей двух точек АТТ.

БИЛЕТ 8.

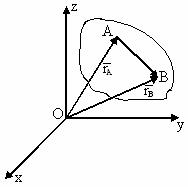
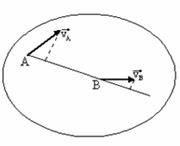
Пусть 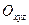- неподвижная система координат. Точки А и В принадлежат АТТ.

,

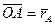
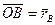
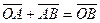
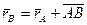
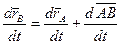
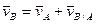
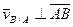, так как 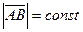(из определения АТТ).

Точка В относительно точки А движется по окружности постоянного радиуса.

Теорема (о проекциях скоростей на прямую, их соединяющую).

Проекции скоростей двух точек твёрдого тела на прямую, их соединяющую равны между собой.

Доказательство.

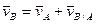
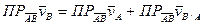
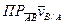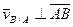
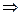
=0, так как 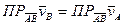, что и требовалось доказать.

БИЛЕТ 9.

Проведем дифференцирование формулы Эйлера.

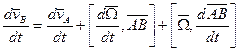
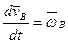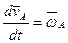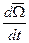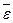, , = - угловое ускорение АТТ, = .

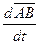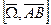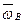
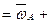
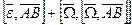- формула Ривальса.

где 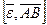- тангенциальное ускорение, 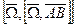- осестремительное ускорение.

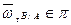
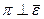, прох. через В.

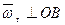
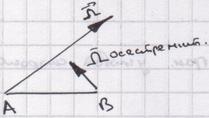
БИЛЕТ 10.

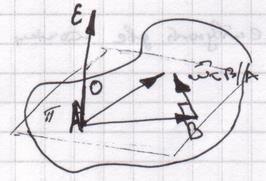
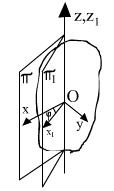
Поступательным движением АТТ называется такое движение АТТ, при котором любая прямая, проведённая в АТТ, остаётся параллельной своему начальному положению.

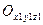- подвижный трехгранник, связанный с АТТ. 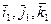- единичные вектора подвижной системы координат, не меняющиеся по направлению, а также постоянные по длине.

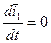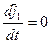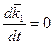
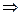
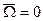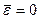
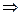
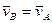
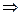, , , траектории всех точек совпадают с точностью до параллельного переноса.

БИЛЕТ 11.

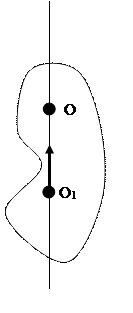
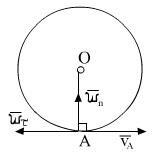
Вращающим движением а.т.т. относительно неподвижной оси называется

такое движение, когда в теле существует такие 2 т-ки, такие что

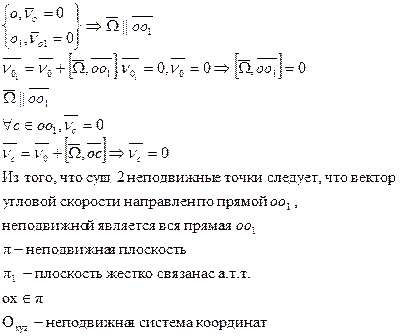
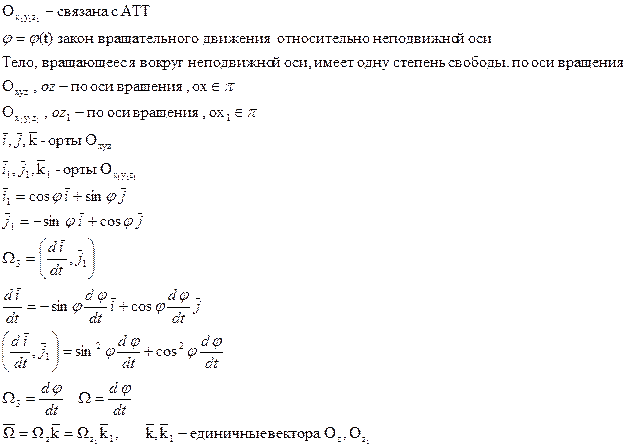
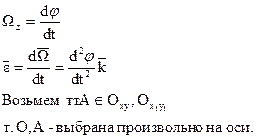
т. А движется по окружности, т.к. расстояние от точки О до А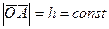

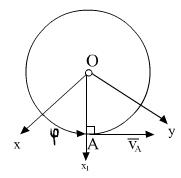
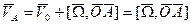
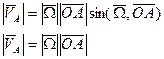
Величина скорости точки = модулю расстояния угловой скорости

и расстояния до оси вращения.

Вектор скорости т. А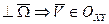

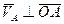
По формуле Ривальса:

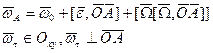
Вторая составляющая ускорения называется осестремительным ускорением.

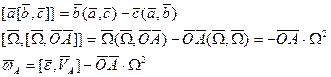
БИЛЕТ 12.