Сложное движение материальной точки

Сложным движением материальной точки называется движение, которое складывается из движения точки относительно подвижной с.к. и движения точки вместе с подвижной с.к.

Движение точки относительно неподвижной с.к. называется абсолютным движением.

Движение точки относительно подвижной с.к. называется относительным движением.

Движение точки с подвижной с.к. называется переносным движением.

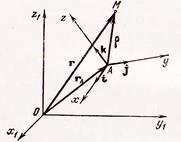Если радиус-вектор 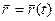определяет положение точки М по отношению к системе координат 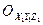, радиус-вектор 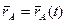определяет положение начала системы координат 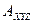в системе 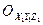, а радиус-вектор 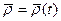опре­деляет положение точки М в системе координат 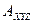, то

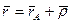
Пусть координаты точки в подвиж­ной системе координат будут 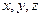тогда

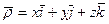
где 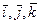- единичные векторы осей подвижной системы координат. По определению абсолютная производная радиуса-вектора по времени будет абсолютной скоростью точки. Следовательно, диффе­ренцируя равенство по времени, найдем абсолютную скорость точки

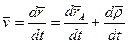
Так как вектор 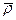определен в подвижной системе координат, то для нахождения абсолютной производной от него воспользуемся формулой

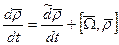
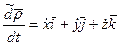
представляет собой относительную производную от 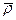по времени.

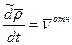- скорость точки с относительной с.к.-относительная скорость

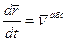-скорость точки относительно неподвижной с.к.- абсолютная скорость точки

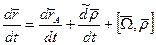
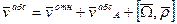
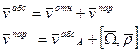
Переносной скоростью называется абсолютная скорость точки принадлежащей подвижной с.к., в которой в данный момент находиться точка.

Абсолютная скорость точки в сложном движении равна геометрической сумме скорости точки относительной и переносной.

БИЛЕТ 15.

Будем называть сложным или «абсолютным» движением точки ее движение по отношению к системе координат, выбранной за основ­ную. Движение точки по отношению к подвижной системе координат будем называть относительным.

Под переносным, движением будем понимать движение подвижной системы координат относительно неподвижной.

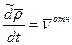- скорость точки с относительной с.к.-относительная скорость

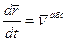-скорость точки относительно неподвижной с.к.- абсолютная скорость точки

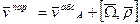-переносной скоростью называется абсолютная скорость точки принадлежащей подвижной с.к., в которой в данный момент находиться точка.

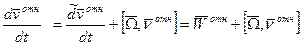
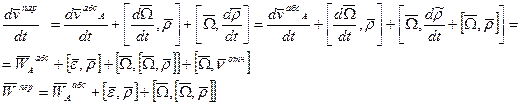
Ускорение точки принадлежащей подвижной с.к. и находящаяся в данный момент там же где находиться точка M – переносное ускорение.

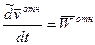-локальная производная относительно скорости.

Относительным ускорением называется ускорение точки относительно подвижной с.к.

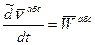-абсолютное ускорение

Абсолютным ускорением называется ускорение точки относительно неподвижной с.к.