Естественный способ задания движения точки.
Движение точки заданно естественно, если:
1) Задана траектория
2) Начало отсчета
3) Задано направление отсчета
4) Известна длина дуги как функция времени.
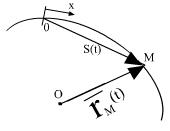
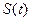 - естественный закон движения точки.
- естественный закон движения точки. 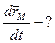 .
.
Каждое положение точки на траектории характеризуется своим радиус-вектором. 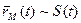 ,
, 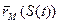 .
.
Зависимость точки 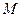 от координаты
от координаты 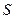 на траектории.
на траектории.
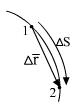
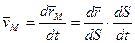 ,
, 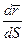 - вектор.
- вектор.
Так как длина дуги стремится к длине секущей при сближении точек (для достаточно гладких кривых), то длина этого вектора:
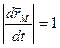 . Вектор
. Вектор 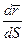 - единичный вектор.
- единичный вектор.
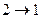
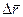 стремится к касательной в точке 1.
стремится к касательной в точке 1.
В каждой точке может быть введен 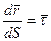 - единичный вектор касательной.
- единичный вектор касательной.
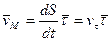 .
. 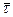 направлен в сторону увеличения
направлен в сторону увеличения 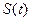 .
. 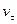 - проекция вектора скорости на направление касательной.
- проекция вектора скорости на направление касательной.
 Если
Если 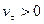 , то
, то 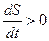 . Если же
. Если же 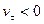 , то
, то 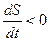 .
. 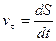
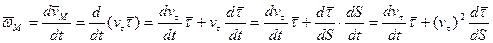
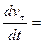
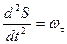 .
. 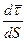 -вектор
-вектор 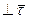 .
.
Вектор 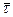 при движении вдоль траектории не изменяется по величине, а изменяется только по направлению, поэтому
при движении вдоль траектории не изменяется по величине, а изменяется только по направлению, поэтому 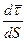
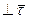 .
.
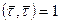
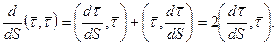
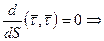
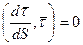
Скалярное произведение двух не нулевых векторов равно нулю, если угол между ними 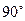
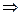
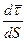
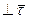 .
.
Вектор постоянной длины и переменного направления. Если его начало закрепить, то при движении он будет описывать сферу. Производная вектора есть скорость конца вектора, то есть величина, вектор которой направлен по касательной к сфере, а значит 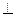 -ый измен. вектору.
-ый измен. вектору.
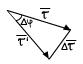
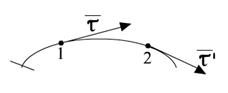
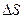
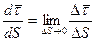 ,
, 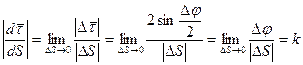 - кривизна траектории.
- кривизна траектории.
Если кривая достаточно гладкая, т.е. вектор касательной резко не изменяет своего положения, то на малом перемещении 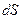 угол изменяется на малую величину.
угол изменяется на малую величину.
Кривизна траектории характеризует изменение направления вектора 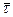 вдоль траектории.
вдоль траектории.
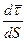
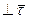 . ,
. , 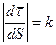 .
. 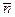 - единичный вектор.
- единичный вектор. 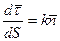 .
.
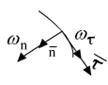
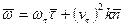
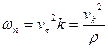 , где
, где 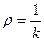 . Если движение по окружности, то
. Если движение по окружности, то 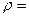 радиусу окружности.
радиусу окружности.
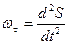 ,
, 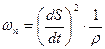 .
.
БИЛЕТ 3.
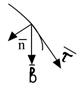 Естественный трехгранник (трехгранник Дарбу). Естественный способ задания движения точки.
Естественный трехгранник (трехгранник Дарбу). Естественный способ задания движения точки.
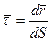 ,
, 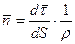 .
. 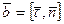 - единичный вектор бинормаль.
- единичный вектор бинормаль.
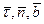 образуют правый трехгранник. – сопровождающий трехгранник или трехгранник Дарбу.
образуют правый трехгранник. – сопровождающий трехгранник или трехгранник Дарбу. 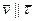 ,
, 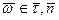 .
.
Плоскость, проходящая через вектора 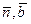 - нормальная плоскость.
- нормальная плоскость.
Плоскость, проходящая через вектора 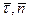 - соприкасающаяся плоскость.
- соприкасающаяся плоскость.
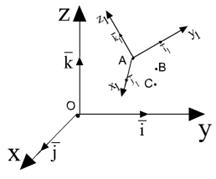 Абсолютно твердым телом называется система материальных точек, растояние между которыми остается неизменным все время движения.
Абсолютно твердым телом называется система материальных точек, растояние между которыми остается неизменным все время движения.
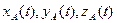
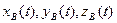
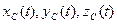
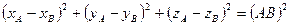 (1)
(1)
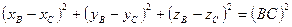 (2)
(2)
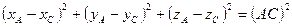 (3)
(3)
9 координат, удовл. 3 уравнениям 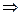 6 свободных.
6 свободных.
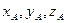 - независимые.
- независимые.
В векторных пределах свободно можно выбрать 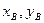 , затем из (1) найти
, затем из (1) найти 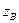 .
.
(2) и (3) ограничив 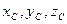
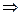 только одну из них можно выбрать свободной.
только одну из них можно выбрать свободной.
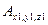 - жестко связ с АТТ.
- жестко связ с АТТ.
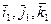 - единичные вектора
- единичные вектора 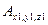 .
.
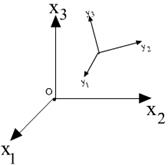
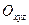 - неподвижные оси,
- неподвижные оси, 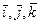 - единичные вектора неподвижных осей.
- единичные вектора неподвижных осей.
Координаты начала подвижной системы координат.
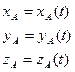
Матрицей ориентации (матрицей направляющих косинусов) трехгранника называется
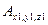 относительно
относительно 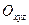 .
.
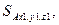
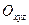 =
= 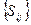
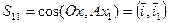
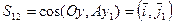
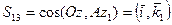
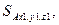
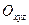 =
= 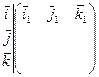 - матрица 3х3
- матрица 3х3
Независимыми являются только три.
В силу свойств матрицей направляющих косинусов.
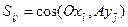
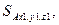
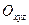 =
= 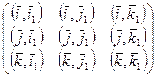
Пусть даны вектора 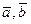 .
.
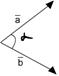 Определение: Скалярное произведение векторов
Определение: Скалярное произведение векторов 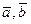 :
: 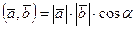 .
.
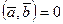 , если
, если 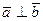
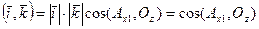 =
=
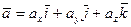 ,
, 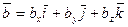
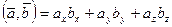
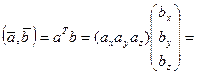 число.
число.
Векторным произведением двух векторов называется вектор, обладающий следующими свойствами:
1). Этот вектор перпендикулярен плоскости векторов 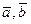 .
.
2). Вектора 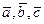 составляют правую тройку векторов.
составляют правую тройку векторов.
3). Модуль 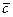 равен модулю
равен модулю 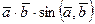 . Другими словами,
. Другими словами, 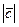 равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах 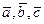 .
.
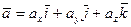 ,
,
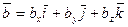
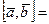
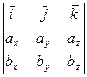 .
.
БИЛЕТ 4.
Дата добавления: 2016-04-23; просмотров: 873;
