Механический и геометрический смысл производной
Обращаясь к рассмотренным ранее задачам, приводящим к понятию производной, можно сформулировать следующие утверждения.
1) Скорость 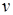 прямолинейного движения точки есть производная пути
прямолинейного движения точки есть производная пути 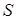 по времени
по времени 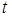 :
: 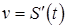 . Это механический смысл производной. Поэтому производную любой функции называют скоростью изменения этой функции.
. Это механический смысл производной. Поэтому производную любой функции называют скоростью изменения этой функции.
2) Угловой коэффициент невертикальной касательной к непрерывной кривой 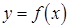 в точке с абсциссой
в точке с абсциссой 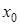 есть производная
есть производная 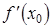 , т.е.
, т.е. 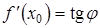 . Это геометрический смысл производной.
. Это геометрический смысл производной.
Известно, что уравнение прямой, проходящей через точку 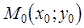 с угловым коэффициентом
с угловым коэффициентом 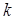 имеет вид:
имеет вид: 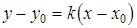 . С учетом этой формулы уравнение касательной к кривой
. С учетом этой формулы уравнение касательной к кривой 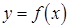 в точке
в точке 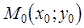 принимает вид:
принимает вид:
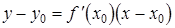
Нормалью к кривой в данной точке называется прямая, проходящая через данную точку перпендикулярно к касательной в этой точке.
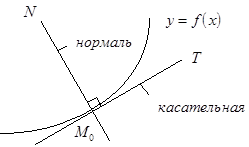
|
Угловые коэффициенты взаимно перпендикулярных прямых связаны соотношением 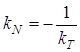 , откуда
, откуда 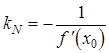 . Следовательно, если
. Следовательно, если 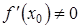 , то уравнение нормали к кривой
, то уравнение нормали к кривой 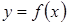 в точке
в точке 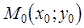 можно записать в виде
можно записать в виде
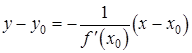 .
.
Пример. Написать уравнения касательной и нормали к кривой 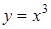 в точке
в точке 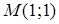 .
.
Так как 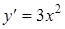 , то угловой коэффициент касательной в указанной точке
, то угловой коэффициент касательной в указанной точке 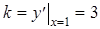 . Следовательно, уравнение касательной
. Следовательно, уравнение касательной
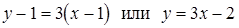 .
.
Уравнение нормали 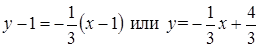 .
.
Дата добавления: 2016-10-17; просмотров: 841;
