Производная сложной функции
Пусть  . Тогда функция
. Тогда функция 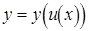 будет сложной функцией от x.
будет сложной функцией от x.
Если функция  дифференцируема в точке x, а функция
дифференцируема в точке x, а функция  дифференцируема в точке u, то
дифференцируема в точке u, то 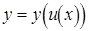 тоже дифференцируема в точке x, причем
тоже дифференцируема в точке x, причем
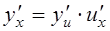 .
.
Примеры.
1. 
Полагаем 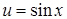 , тогда
, тогда 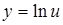 . Следовательно
. Следовательно
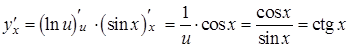 .
.
При достаточном навыке промежуточную переменную u не пишут, вводя ее лишь мысленно.
2. 
 .
.
Логарифмическое дифференцирование
Показательно-степенной функцией называется функция вида  , где
, где 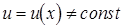 ,
,  – дифференцируемые функции и
– дифференцируемые функции и 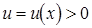 .
.
Для нахождения производной такой функции ее сначала логарифмируют, а затем дифференцируют полученное равенство.
Логарифмическое дифференцирование применяется также для функций, состоящих из большого числа сомножителей или являющихся отношением произведений нескольких функций.
Примеры.
1. Найти производную функции  .
.
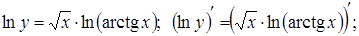
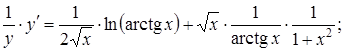
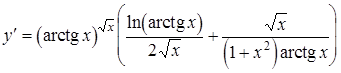 .
.
2. Найти производную функции 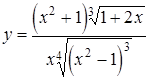 .
.
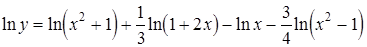 ;
;
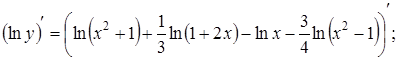
 ;
;
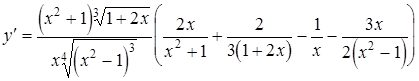 .
.
Замечание. При решении применялись следующие свойства логарифмов:
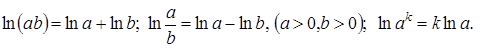
Дифференциал
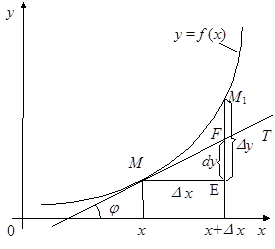
|
К графику непрерывной функции 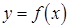 в точке
в точке 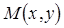 проведем касательную MT, обозначив через j ее угол наклона к положительному направлению оси Ох. Так как
проведем касательную MT, обозначив через j ее угол наклона к положительному направлению оси Ох. Так как 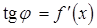 , то из треугольника MEF следует, что
, то из треугольника MEF следует, что
 .
.
Введем обозначение
 .
.
Это выражение называется дифференциалом функции 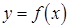 . Итак
. Итак
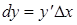 .
.
Замечая, что  , т.е. что дифференциал независимой переменной равен ее приращению, получим
, т.е. что дифференциал независимой переменной равен ее приращению, получим
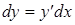 .
.
Таким образом, дифференциал функции равен произведению ее производной на дифференциал (или приращение) независимой переменной.
Из последней формулы следует, что 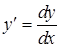 , т.е. производная функции равна отношению дифференциала этой функции к дифференциалу аргумента.
, т.е. производная функции равна отношению дифференциала этой функции к дифференциалу аргумента.
Дифференциал функции dy геометрически представляет собой приращение ординаты касательной, соответствующее приращению аргумента Dх.
Из рисунка видно, что при достаточно малом Dх по абсолютной величине можно взять приращение функции 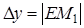 приближенно равным ее дифференциалу, т.е.
приближенно равным ее дифференциалу, т.е.
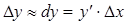 .
.
Рассмотрим сложную функцию  , где
, где  , причем
, причем  дифференцируема по u, а
дифференцируема по u, а  – по х. По правилу дифференцирования сложной функции
– по х. По правилу дифференцирования сложной функции
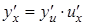 .
.
Умножим это равенство на dx:
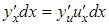
Так как  (по определению дифференциала), то
(по определению дифференциала), то
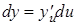 или
или 
Таким образом, дифференциал сложной функции имеет тот же вид, если бы переменная u была не промежуточным аргументом, а независимой переменной.
Это свойство дифференциала называется инвариантностью (неизменяемостью) формы дифференциала.
Пример. 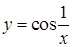 .
.
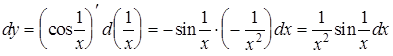
Все правила дифференцирования можно записать для дифференциалов.
Пусть 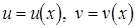 – дифференцируемы в точке х. Тогда
– дифференцируемы в точке х. Тогда
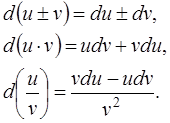
Докажем второе правило.
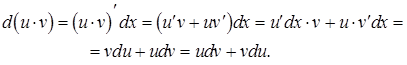
Дата добавления: 2016-10-17; просмотров: 864;
