Задача о касательной к данной кривой
Производная и дифференциал функции одной переменной
Задача о скорости движущейся точки
Пусть  – закон прямолинейного движения материальной точки. Обозначим через
– закон прямолинейного движения материальной точки. Обозначим через 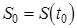 путь, пройденный точкой за время
путь, пройденный точкой за время 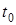 , а через
, а через 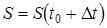 путь, пройденный за время
путь, пройденный за время 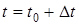 . Тогда за время
. Тогда за время 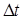 точка пройдет путь
точка пройдет путь 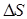 , равный:
, равный: 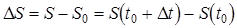 . Отношение
. Отношение 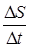 называется средней скоростью точки за время от
называется средней скоростью точки за время от 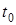 до
до 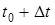 . Чем меньше
. Чем меньше 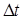 , т.е. чем короче промежуток времени от
, т.е. чем короче промежуток времени от 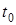 до
до 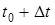 , тем лучше средняя скорость характеризует движение точки в момент времени
, тем лучше средняя скорость характеризует движение точки в момент времени 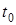 . Поэтому естественно ввести понятие скорости
. Поэтому естественно ввести понятие скорости 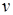 в данный момент
в данный момент 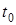 , определив ее как предел средней скорости за промежуток от
, определив ее как предел средней скорости за промежуток от 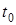 до
до 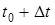 , когда
, когда 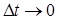 :
:
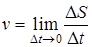 .
.
Величина 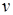 называется мгновенной скоростью точки в данный момент
называется мгновенной скоростью точки в данный момент 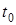 .
.
Задача о касательной к данной кривой
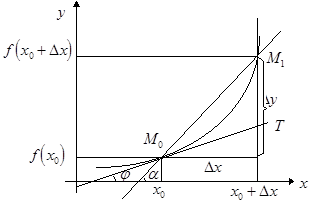
|
Пусть на плоскости 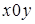 задана непрерывная кривая уравнением
задана непрерывная кривая уравнением 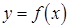 . Требуется провести невертикальную касательную к данной кривой в точке
. Требуется провести невертикальную касательную к данной кривой в точке 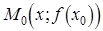 . Так как точка касания
. Так как точка касания  дана, то для решения задачи требуется найти угловой коэффициент
дана, то для решения задачи требуется найти угловой коэффициент 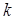 касательной. Из геометрии известно, что
касательной. Из геометрии известно, что 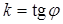 , где
, где 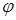 – угол наклона касательной к положительному направлению оси
– угол наклона касательной к положительному направлению оси 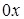 (см. рис.). Через точки
(см. рис.). Через точки 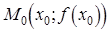 и
и 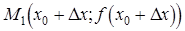 проведем секущую
проведем секущую 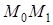 , где
, где 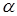 – угол, образованный секущей с положительным направлением оси
– угол, образованный секущей с положительным направлением оси 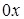 . Из рисунка видно, что
. Из рисунка видно, что 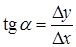 , где
, где 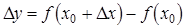 . Угловой коэффициент касательной
. Угловой коэффициент касательной 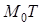 к данной кривой в точке
к данной кривой в точке  может быть найден на основании следующего определения.
может быть найден на основании следующего определения.
Касательной 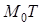 к кривой
к кривой 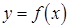 в точке
в точке  называется предельное положение секущей
называется предельное положение секущей 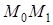 , когда точка
, когда точка 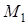 стремится к точке
стремится к точке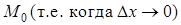 . Отсюда следует, что
. Отсюда следует, что 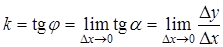 .
.
Дата добавления: 2016-10-17; просмотров: 1894;
