Общие правила дифференцирования
Производные любых функций можно найти непосредственно по определению, как показано в п.4.4. Однако каждый раз делать это весьма затруднительно, поэтому для дифференцирования произвольных функций можно воспользоваться таблицей производных элементарных функций и правилами дифференцирования.
Пусть функции  и
и 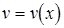 дифференцируемы в точке
дифференцируемы в точке 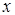 . Тогда их сумма, разность, произведение и частное
. Тогда их сумма, разность, произведение и частное 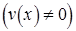 также дифференцируемы в точке
также дифференцируемы в точке 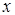 , причем
, причем


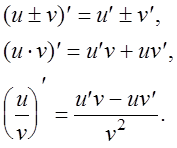
Для примера выведем правило дифференцирования произведения двух функций. Пусть 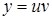 . Придадим аргументу
. Придадим аргументу 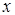 произвольное приращение
произвольное приращение 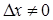 , тогда в результате этого функции
, тогда в результате этого функции 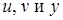 получат соответственно приращения
получат соответственно приращения 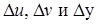 :
:
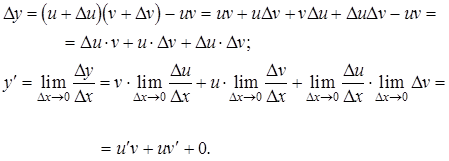
Таким образом, 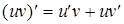 . При выводе использовано условие дифференцируемости, а, следовательно, и непрерывности функции
. При выводе использовано условие дифференцируемости, а, следовательно, и непрерывности функции 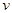 , в силу чего
, в силу чего 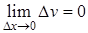 . В частности, из доказанной формулы вытекает правило:
. В частности, из доказанной формулы вытекает правило:
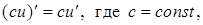
т.е. постоянный множитель можно выносить за знак производной.
Таблица производных элементарных функций
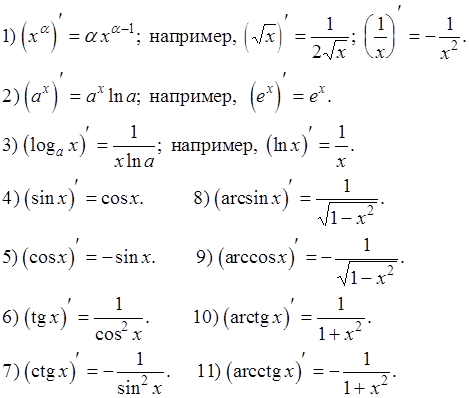
Замечание. Напомним свойства степеней и корней, используемые при дифференцировании функций:
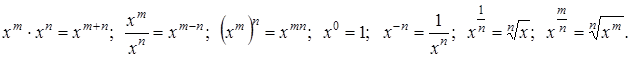
Приведем примеры нахождения производных.
1) 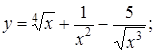 .
.
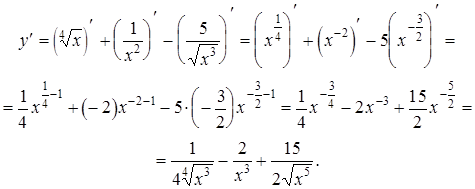
2) 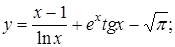
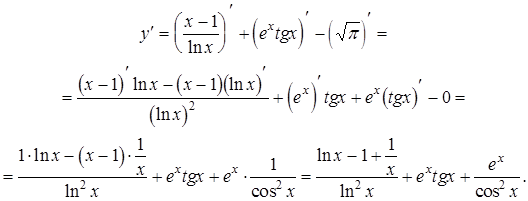
Дата добавления: 2016-10-17; просмотров: 1481;
