Точки перегиба графика функции
Определение. Кривая называется выпуклой (вогнутой) на интервале 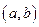 , если все ее точки лежат не выше (не ниже) любой ее касательной на этом интервале.
, если все ее точки лежат не выше (не ниже) любой ее касательной на этом интервале.
Теорема 1. Если во всех точках интервала 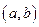 вторая производная функции
вторая производная функции 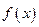 отрицательна, то кривая
отрицательна, то кривая 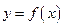 обращена выпуклостью вверх (выпукла).
обращена выпуклостью вверх (выпукла).
Доказательство. Пусть 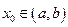 . Проведем касательную к кривой в этой точке. Уравнение кривой:
. Проведем касательную к кривой в этой точке. Уравнение кривой: 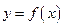 . Уравнение касательной:
. Уравнение касательной: 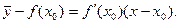
Следует доказать, что 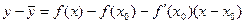 .
.
По теореме Лагранжа для 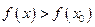 имеем
имеем 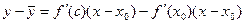 ,
, 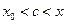 или
или 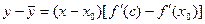 .
.
По теореме Лагранжа для 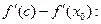
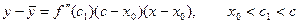
Пусть 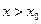 тогда
тогда 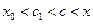 . Т.к.
. Т.к. 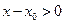 и
и 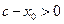 и, кроме того по условию
и, кроме того по условию
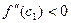 . Следовательно,
. Следовательно, 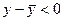 .
.
Пусть 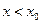 тогда
тогда 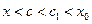 и
и 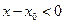 ,
, 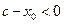 , т.к. по условию
, т.к. по условию 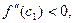 то
то
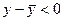 .
.
Аналогично доказывается, что если 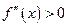 на интервале
на интервале 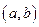 , то кривая
, то кривая 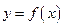 вогнута на интервале
вогнута на интервале 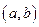 . Теорема доказана.
. Теорема доказана.
Определение. Точка, при переходе через которую направление вогнутости кривой меняется на противоположное, называется точкой перегиба.
Очевидно, что в точке перегиба касательная пересекает кривую.
Теорема 2. Пусть кривая определяется уравнением 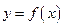 . Если вторая производная
. Если вторая производная 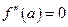 или
или 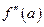 не существует и при переходе через точку
не существует и при переходе через точку 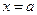
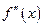 меняет знак, то точка кривой с абсциссой
меняет знак, то точка кривой с абсциссой 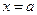 является точкой перегиба.
является точкой перегиба.
Доказательство.
1) Пусть 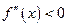 при
при 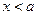 и
и 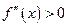 при
при 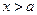 . Тогда при
. Тогда при
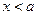 кривая выпукла, а при
кривая выпукла, а при 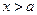 кривая вогнута, т.е. точка
кривая вогнута, т.е. точка 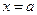 – точка перегиба.
– точка перегиба.
1) Пусть 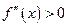 при
при 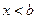 и
и 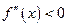 при
при 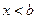 . Тогда при
. Тогда при 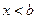 кривая обращена выпуклостью вниз, а при
кривая обращена выпуклостью вниз, а при 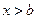 – выпуклостью вверх. Тогда
– выпуклостью вверх. Тогда 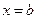 – точка перегиба.
– точка перегиба.
Теорема доказана.
Дата добавления: 2016-05-05; просмотров: 691;
