Шесть членов разложения
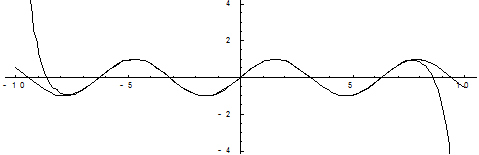
Десять членов разложения
Чтобы получить наиболее точное значение функции при наименьшем количестве членов разложения надо в формуле Тейлора в качестве параметра а выбрать такое число, которое достаточно близко к значению 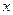 , и значение функции от этого числа легко вычисляется.
, и значение функции от этого числа легко вычисляется.
Для примера вычислим значение 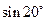 .
.
Предварительно переведем угол 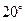 в радианы:
в радианы: 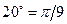 .
.
Применим разложение в ряд Тейлора, ограничившись тремя первыми членами разложения:
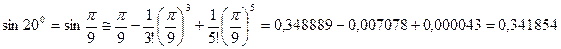 .
.
В четырехзначных таблицах Брадиса для синуса этого угла указано значение 0,3420.
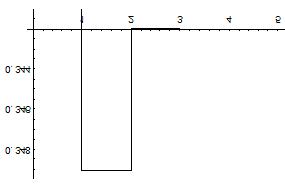
На графике показано изменение значений разложения в ряд Тейлора в зависимости от количества членов разложения. Следоватеельно, если ограничиться тремя членами разложения, то достигается точность до 0,0002.
Выше говорилось, что при 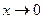 функция
функция 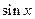 является бесконечно малой и может при вычислении быть заменена на эквивалентную ей бесконечно малую функцию х. Теперь видно, что при
является бесконечно малой и может при вычислении быть заменена на эквивалентную ей бесконечно малую функцию х. Теперь видно, что при 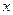 , близких к нулю, можно практически без потери в точности ограничиться первым членом разложения, т.е.
, близких к нулю, можно практически без потери в точности ограничиться первым членом разложения, т.е. 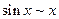 .
.
Пример. Вычислить 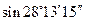 .
.
Для того чтобы представить заданный угол в радианах, воспользуемся соотношениями:
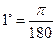 ;
; 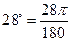 ;
;
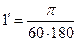 ;
; 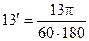 ;
;
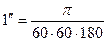 ;
; 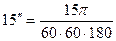 ;
;
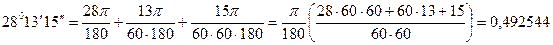 рад
рад
Если при разложении по формуле Тейлора ограничиться тремя первыми членами, получим: 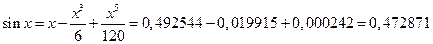 .
.
Сравнивая полученный результат с точным значением синуса этого угла,
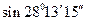 = 0,472869017612759812,
= 0,472869017612759812,
видим, что даже при ограничении всего тремя членами разложения, точность составила 0,000002, что более чем достаточно для большинства практических технических задач.
Функция 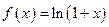
Получаем: 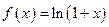 ;
; 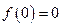 ;
;
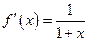 ;
; 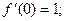
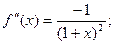
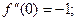
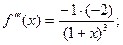
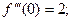
………………………………………
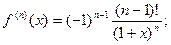
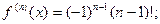
Следовательно: 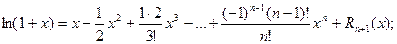
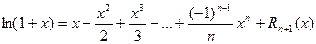 ;
;
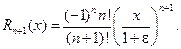
Полученная формула позволяет находить значения любых логарифмов (не только натуральных) с любой степенью точности. Ниже представлен пример вычисления натурального логарифма 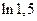 . Сначала получено точное значение, затем – расчет по полученной выше формуле, ограничившись пятью членами разложения. Точность достигает 0,0003.
. Сначала получено точное значение, затем – расчет по полученной выше формуле, ограничившись пятью членами разложения. Точность достигает 0,0003.
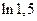 = 0,405465108108164381.
= 0,405465108108164381.
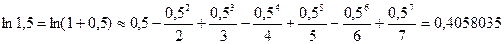 .
.
Разложение различных функций по формулам Тейлора и Маклорена приводится в специальных таблицах, однако, формула Тейлора настолько удобна, что для подавляющего большинства функций разложение может быть легко найдено непосредственно.
Дата добавления: 2016-05-05; просмотров: 703;
