Представление некоторых элементарных функций
По формуле Тейлора
Применение формулы Тейлора для разложения функций в степенной ряд широко используется и имеет огромное значение при проведении различных математических расчетов. Непосредственное вычисление интегралов некоторых функций может быть сопряжено со значительными трудностями, а замена функции степенным рядом позволяет значительно упростить задачу. Нахождение значений тригонометрических, обратных тригонометрических, логарифмических функций также может быть сведено к нахождению значений соответствующих многочленов.
Если при разложении в ряд взять достаточное количество слагаемых, то значение функции может быть найдено с любой наперед заданной точностью. Практически можно сказать, что для нахождения значения любой функции с разумной степенью точности (предполагается, что точность, превышающая 10 – 20 знаков после десятичной точки, необходима очень редко) достаточно 4-10 членов разложения в ряд.
Применение принципа разложения в ряд позволяет производить вычисления на ЭВМ в режиме реального времени, что немаловажно при решении конкретных технических задач.
Функция 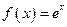 .
.
Находим: 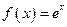 ,
, 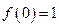 ,
,
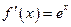 ,
, 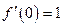 ,
,
……………………
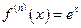 ,
, 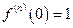 ,
,
Тогда: 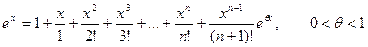 .
.
Пример. Найдем значение числа 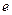 . В полученной выше формуле положим
. В полученной выше формуле положим 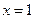 .
.
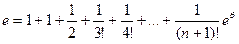
Для 8 членов разложения: e = 2,71827876984127003.
Для 10 членов разложения: e = 2,71828180114638451.
Для 100 членов разложения: e = 2,71828182845904553.
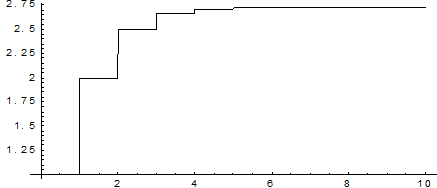
На графике показаны значения числа е с точностью в зависимости от числа членов разложения в ряд Тейлора.
Следовательно, для достижения точности, достаточной для решения большинства практических задач, можно ограничиться 6-7 – ю членами ряда.
Функция 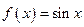
Получаем 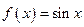 ;
; 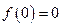 ;
;
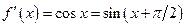 ;
; 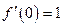 ;
;
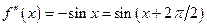 ;
; 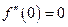 ;
;
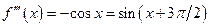 ;
; 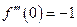 ;
;
…………………………………………
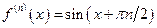 ;
; 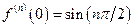 ;
;
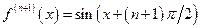 ;
; 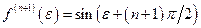 ;
;
Следовательно 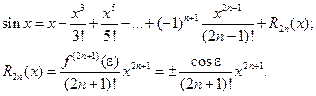
Функция 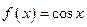
Для функции 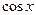 , применив аналогичные преобразования, получим:
, применив аналогичные преобразования, получим:

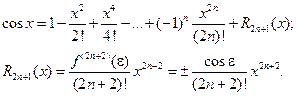
Функция 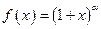
( 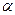 - действительное число)
- действительное число)
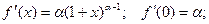
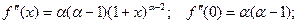
…………………………………………………..
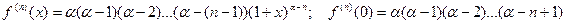 .
.
Тогда:
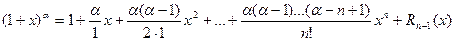 ;
;
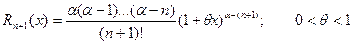 .
.
Если в полученной формуле принять 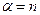 , где
, где 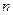 - натуральное число и
- натуральное число и 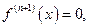 то
то 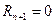 , тогда
, тогда
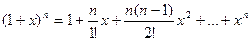 .
.
Получили формулу, известную как бином Ньютона.
Пример. Применить полученную формулу для нахождения синуса любого угла с любой степенью точности.
На приведенных ниже графиках представлено сравнение точного значения функции и значения разложения в ряд Тейлора при различном количестве членов разложения.
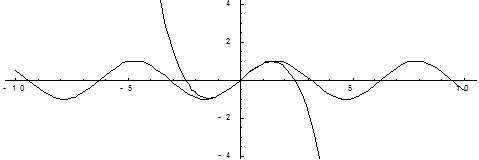
Дата добавления: 2016-05-05; просмотров: 603;
