Теоретичні значення Q – критерію. при різних довірчих імовірностях Р
| n | Q( n. P ) | ||
| P = 0.90 | p = 0.95 | p = 0.99 | |
| 0.89 | 0.94 | 0.99 | |
| 0.68 | 0.77 | 0.89 | |
| 0.56 | 0.64 | 0.76 | |
| 0.48 | 0.56 | 0.70 | |
| 0.43 | 0.51 | 0.64 | |
| 0.48 | 0.55 | 0.68 | |
| 0.44 | 0.51 | 0.64 | |
| 0.41 | 0.48 | 0.60 |
Щоб знайти середнє значення абсолютної похибки, виконуюють такі обчислення:
- розраховють дисперсію значень вимірюваного параметра, ( рівняння (5, 5а));
- розраховють стандартне відхилення, (рівняння (6)).
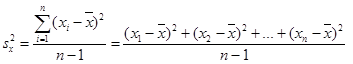 (5)
(5)
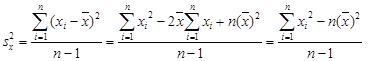 (5a)
(5a)
n –1 = f – ступінь свободи.
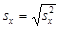 (6)
(6)
Величинуsxще називають «середньоквадратичне відхилення»або «середньоквадратична похибка».
Коли відомі середнє значення і дисперсія, можна використати більш строгий підхід до виявлення грубих помилок – «промахів». Розраховють з вибірки експериментальних значень виміряного параметра значення β критерію для xk = xmax, xmin або X1, Xn з ранжированого ряду.
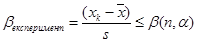 .(7)
.(7)
де, α = 1−P – імовірність отримати «промах»;
Розраховане значення порівнюють із теоретичним значенням (див. таблицю 2).
У випадку, коли сумнівне значення параметра признається похибкою, його виключають із вибірки і по n-1 значенням обчислюють нові значення середнього, дисперсії та стандартного відхилення.
Використовуючи середнє значення і стандартне відхилення формують інтервал (довірчий інтервал) значень навколо середної величини, який з заданою наперед імовірністю (P = 0,95; 0,99 ) накриває дійсне значення вимірюваного параметра. При розрахунках граничних значень довірчого інтервалу використовують рівняння (8):
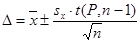 (8)
(8)
Значення t (P, n – 1) наведено в таблиці 3. Цей критерій називають «t-критерій Стьюдента». «Стьюдент» – псевдонім англійського математика Госсета.
Таблиця 2
Значення критерію грубої похибки β
| n | β | ||
| α = 0.05 | α = 0.01 | α = 0.001 | |
| 15.561 | 77.964 | 779.696 | |
| 4.969 | 11.460 | 36.486 | |
| 3.558 | 6.530 | 14.468 | |
| 3.041 | 5.043 | 9.432 | |
| 2.777 | 4.355 | 7.409 | |
| 2.616 | 3.963 | 6.370 | |
| 2.508 | 3.711 | 5.733 | |
| 2.431 | 3.536 | 5.314 | |
| 2.372 | 3.409 | 5.014 | |
| 3.327 | 3.310 | 4.791 | |
| 2.291 | 3.233 | 4.618 | |
| 2.261 | 3.170 | 4.481 | |
| 2.236 | 3.118 | 4.369 | |
| 2.215 | 3.075 | 4.276 | |
| 2.197 | 3.038 | 4.198 | |
| 2.181 | 3.006 | 4.131 | |
| 2.168 | 2.997 | 4.074 | |
| 2.156 | 2.953 | 4.024 | |
| 2.145 | 2.932 | 3.979 | |
| 2.135 | 2.912 | 3.941 | |
| 2.127 | 2.895 | 3.905 | |
| 2.119 | 2.880 | 3.874 | |
| 2.112 | 2.865 | 3.845 | |
| 2.105 | 2.852 | 3.819 | |
| 2.099 | 2.840 | 3.796 | |
| 2.094 | 2.830 | 3.775 | |
| 2.088 | 2.820 | 3.755 | |
| 2.083 | 2.810 | 3.737 | |
| 2.079 | 2.802 | 3.719 | |
| 2.048 | 2.742 | 3.602 | |
| 2.018 | 2.683 | 3.402 | |
| 1.988 | 2.628 | 3.388 | |
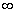
| 1.960 | 2.576 | 3.291 |
Таблиця 3
Дата добавления: 2016-08-07; просмотров: 746;
