Значення t-критерію Стьюдента
| f | p | ||||
| 0.90 | 0.95 | 0.99 | 0.995 | 0.999 | |
| 6.3130 | 12.7060 | 63.6560 | 127.6560 | 636.619 | |
| 2.9200 | 4.3020 | 9.9240 | 14.0890 | 31.599 | |
| 2.35340 | 3.1820 | 5.8400 | 7.4580 | 12.924 | |
| 2.13180 | 2.7760 | 4.6040 | 5.5970 | 8.610 | |
| 2.01500 | 2.5700 | 4.0321 | 4.7730 | 6.863 | |
| 1.9430 | 2.4460 | 3.7070 | 4.3160 | 5.958 | |
| 1.8946 | 2.3646 | 3.4995 | 4.2293 | 5.4079 | |
| 1.8596 | 2.3060 | 3.3554 | 3.8320 | 5.0413 | |
| 1.8331 | 2.2622 | 3.2498 | 3.6897 | 4.7800 | |
| 1.8125 | 2.2281 | 3.1693 | 3.5814 | 4.5869 | |
| 1.7950 | 2.2010 | 3.1050 | 3.4960 | 4.4370 | |
| 1.7823 | 2.1788 | 3.0845 | 3.4284 | 4.1780 | |
| 1.7709 | 2.1604 | 3.1123 | 3.3725 | 4.2200 | |
| 1.7613 | 2.1448 | 2.9760 | 3.3257 | 4.1400 | |
| 1.7530 | 2.1314 | 2.9467 | 3.2860 | 4.0720 | |
| 1.7450 | 2.1190 | 2.9200 | 3.2520 | 4.0150 | |
| 1.7396 | 2.1098 | 2.8982 | 3.2224 | 3.9650 | |
| 1.7341 | 2.1009 | 2.8784 | 3.1966 | 3.9216 | |
| 1.7291 | 2.0930 | 2.8609 | 3.1737 | 3.8834 | |
| 1.7247 | 2.0860 | 2.8453 | 3.1534 | 3.8495 | |
| 1.7200 | 2.0790 | 2.8310 | 3.1350 | 3.8190 | |
| 1.7117 | 2.0739 | 2.8188 | 3.1188 | 3.7921 | |
| 1.7139 | 2.0687 | 2.8073 | 3.1040 | 3.7676 | |
| 1.7109 | 2.0639 | 2.7969 | 3.0905 | 3.7454 | |
| 1.7081 | 2.0595 | 2.7874 | 3.0782 | 3.7251 | |
| 1.6973 | 2.0423 | 2.7500 | 3.0298 | 3.6460 | |
| 1.6839 | 2.0211 | 2.7045 | 3.9712 | 3.5510 | |
| 1.6759 | 2.0086 | 2.6778 | 3.9370 | 3.4060 | |
| 1.6706 | 2.0003 | 2.6603 | 3.9146 | 3.4602 | |
| 1.6689 | 1.9944 | 2.6479 | 3.8987 | 3.4350 | |
| 1.6640 | 1.9900 | 2.6380 | 2.8870 | 3.4160 | |
| 1.6620 | 1.9867 | 2.6316 | 2.8779 | 3.4019 | |
| 1.6602 | 1.9840 | 2.6259 | 2.8707 | 3.3905 |
Приклад 1.При визначенні масової частки іонів цинку(ІІ) в крупі було отримано такі результати: 0,230; 0,239; 0,237; 0,235; 0,237 мг/кг. Зробити статистичну обробку результатів вимірювань.
Розв’язок:Сформуємо ряд за рангом: 0,230, 0,235, 0,237, 0,237, 0,239. Перевіримо крайні значення на можливі похибки (див. рівняння (3)):
.
Це значить, що найбільше і найменше значення в ряді, що виміряли, не є похибками.
Обчислимо середнє значення (див. рівняння (4)):
.
Обчислимо дисперсію (s2ω, див. рівняння (5)) і стандартне відхилення (sω, див. рівняння (6)):
.
І на завершення обчислимо довірчий інтервал
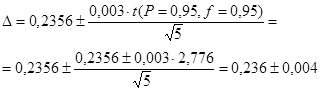
Відповідь: Результат аналізу крупи виражається довірчим інтервалом навколо середньої величини: [0,232 – 0,240], або ω = 0,236 ± 0,004.
Одна з задач, яку можна розв’язати з використанням статистичних методів − це задача про можливість об'єднання двох виборок, отриманих у різних умовах.
Наприклад, одну і ту ж характеристику − масову частку компонента в об’єкті, виміряно двома різними методами: x11, x12, x13,…, x1n; x21, x22, x23,…, x2m. Чи можна об’єднати вибірки в одну, яка має n + m значень?
Розвязання такої задачі передбачає відповіді на два запитання:
‑ чи є вибірки однорідні (виконані з однаковою точністю)?
- чи вибірки не містять систематичних похибок?
Щоб відповісти на ці питання обчислюють середнє значення для кожної вибірки 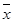 1,
1, 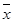 2 та дисперсії
2 та дисперсії 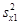 ,
, 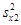 .
.
Співвідношення більшої дисперсії до меншої порівнюють зі статистичним критерієм Фіщера – F(n2-1, n1-1,P)(див. таблицю 4).
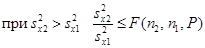
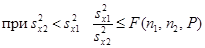 (9)
(9)
Якщо сіввідношення експериментальних дисперсій не перевищує значення критерію Фішера це значить, вибірки однорідні, а значення рівноточні.
Для перевірки можливої систематичної похибки за рівнянням (11) досліджують різницю між середніми значеннями двох виборок. Відношення цієї різниці до середньозваженого стандартного відхиленя (s12) не повинно перевищувати –критерій стьюдента.
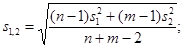 (10)
(10)
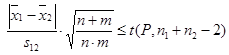 .(11)
.(11)
Виконання умов за рівняннями (9) і (11) дозволяють об’єднати дві вибірки і обчислити для нової об’єднаної вибірки середнє значення і стандартне відхилення.
Приклад 2.Визначити, яка систематична похибка в результатах однієї з виборок не буде помічена при співставленні на об’єднання двох виборок: x1i = 2,39 2,33 2,32 2,39 2,32
x2 i = 2,36 2,40 2,37 2,39 2,30
Розв’язок: Обчислимо середні значення і стандартні відхилення для обох виборок: 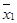 =2,349
=2,349 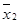 =2,363
=2,363
sx1 = 0,075 sx2 = 0,075. Зрозуміло, що тест на однорідність вибірки прходять. Середньозважене стандартне відхилення залишиться таким же s12 = sx1 = sx2 = 0,075. Різниця між середніми значеннями двох виборок за рівнянням (11) повинна задовольняти умові
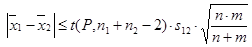 ,
,
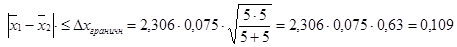 Різниця двох середніх значень:
Різниця двох середніх значень:
Δx12 = 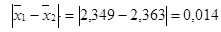 .
.
Значить різниця Δxадд = Δxграничн - Δx12 = 0,095 може бути додана до всіх вимірних значень першої вибірки. Допустима від’ємна систематична похибка для першої вибірки Δxадд = Δxграничн + Δx12 = 0.123. Для другої вибрки допустимі систематичні похибки міняють знак.
Таким чином до всіх вимірних значень першої вибірки можна додати позитивну систематичну похибку Δxадд= 0,095 або негативну систематичну похибку Δxадд= -0,123. до всіх вимірних значень другої вибірки можна додати позитивну систематичну похибку Δxадд=0,123 або негативну систематичну похибку Δxадд= -0,095 і такі систематичні похибки при співставленні цих двох виборок не вдасться виявити за допомогою статистичних методів обробки.
Таблиця 4
значення критерію фішера,
F (f1, f2, P = 0,95 ). 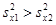
| f1=n-1 | |||||||||||
| f2= m-1 | |||||||||||
| 18.5 | 19.0 | 19.2 | 19.25 | 19.3 | 19.3 | 19.4 | 19.4 | 19.4 | 19.4 | 19.4 | |
| 10.1 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.89 | 8.85 | 8.81 | 8.79 | 8.70 | |
| 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 | 6.00 | 5.96 | 5.86 | |
| 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4.82 | 4.77 | 4.74 | 4.62 | |
| 5.99 | 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 | 4.10 | 4.06 | 3.94 | |
| 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 | 3.68 | 3.64 | 3.51 | |
| 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 | 3.39 | 3.35 | 3.22 | |
| 5.12 | 4.26 | 3.86 | 3.63 | 3.48 | 3.37 | 3.29 | 3.23 | 3.18 | 3.14 | 3.01 | |
| 4.96 | 4.10 | 3.71 | 3.48 | 3.33 | 3.22 | 3.14 | 3.07 | 3.02 | 2.98 | 2.85 | |
| 4.84 | 3.98 | 3.59 | 3.36 | 3.20 | 3.09 | 3.01 | 2.95 | 2.90 | 2.85 | 2.72 | |
| 4.75 | 3.89 | 3.49 | 3.26 | 3.11 | 3.00 | 2.91 | 2.85 | 2.80 | 2.75 | 2.62 | |
| 4.67 | 3.81 | 3.41 | 3.18 | 3.03 | 2.92 | 2.83 | 2.77 | 2.71 | 2.67 | 2.53 | |
| 4.60 | 3.74 | 3.34 | 3.11 | 2.96 | 2.85 | 2.76 | 2.70 | 2.65 | 2.60 | 2.46 | |
| 4.54 | 3.68 | 3.29 | 3.06 | 2.90 | 2.79 | 2.71 | 2.64 | 2.59 | 2.54 | 2.40 |
При обробці результатів хімічного аналізу систематичні похибки повинні бути виявлені й усунуті або, принаймні, оцінені. Один зі способів виявлення систематичної похибки (перевірка правильності) — варіювання величини проби. Подвоюючи (спосіб подвоєння) або збільшуючи розмір проби в кратне число разів, можна виявити по зміні знайденого вмісту компонента, що визначають (див. мал. 1.3) постійну систематичну похибку.
Існує також спосіб «уведено-знайдено», коли до проби, яку аналізують, додається точно відома кількість компонента, який визначають. Компонент повинен бути доданий у тій же формі, в якій він перебуває в аналізованому об’єкті і проведений через усі стадії аналізу. При цьому компонент може бути введений у матрицю зразка, що не містить компонента, який визначають, або доданий до зразка, що містить точно встановлену кількість компонента. Якщо на останній стадії аналізу введена кількість компонента визначається з достатньою точністю, то результат аналізу вважається правильним.
Ще одним способом перевірки правильності є порівняння результату аналізу з результатом, отриманим іншим незалежним методом. При цьому хімік повинен бути впевнений у тому, що обраний для порівняння метод (методика) дає правильний результат і є дійсно незалежним, тобто в основу визначення компонента покладені різні принципи. Наприклад, при перевірці правильності визначення компонента спектрофотометричним методом бажане для порівняння використовувати хроматографічний, полярографічний або потенціометричний метод, але не спектрофотометричний із застосуванням іншого реагенту.
Загальноприйнятий засіб оцінки правильності — аналіз стандартного зразка. Це найбільш надійний спосіб виявлення систематичної похибки. Стандартні зразки виготовляють із матеріалу, сполука й властивості якого надійно встановлені й офіційно засвідчені. Зазвичай стандартні зразки (на один або більше компонентів) аналізують різними методами в декількох лабораторіях, тому вміст компонентів, зазначений у свідоцтві про склад зразка, можна ухвалювати як дійсне значення. Неодмінна умова застосування стандартного зразка в хімічному аналізі − максимальна близькість сполуки й властивостей стандартного зразка і проби. При використанні стандартного зразка для оцінки правильності методу або методики проводять багаторазовий хімічний аналіз зразка й порівнюють знайдений вміст із дійсним (паспортним) вмістом обумовленого компонента.
Оцінка правильності методу або методики повинна проводитися для декількох різних вмістів обумовленого компонента, тобто з використанням двох або декількох стандартних зразків. Стандартні зразки використовують не тільки для перевірки правильності кінцевого результату визначення компонента, але й на окремих стадіях хімічного аналізу з метою виявлення систематичних похибок.
Зараз відомі державні стандартні зразки (зразки 1-го розряду) для металів, сплавів, продуктів і напівпродуктів хімічної промисловості, лікарських препаратів і т. п. Особливо складне виготовлення стандартних зразків складних (багатокомпонентних, багатофазних, нестійких у часі) речовин: руд, гірських порід, харчових продуктів, біомас, об’єктів навколишнього середовища. У цих випадках стандартні зразки виготовляють на основі реальних об'єктів, проводячи багаторазові, складні хімічні аналізи зусиллями різних установ, галузей і навіть країн (створення міжнародних стандартних зразків).
Для розв’язку низки проблем, у тому числі й для перевірки правильності, застосовують стандартні зразки 2-го розряду, створені в окремих галузях народного господарства, наукових і виробничих організаціях, окремих лабораторіях. Хіміки-аналітики іноді використовують для перевірки правильності складені або синтезовані суміші компонентів, надійно проаналізовані хімічні речовини.
1. ГРАВИМЕТРИЧЕСКИЙ АНАЛИЗ
Дата добавления: 2016-08-07; просмотров: 1238;
