Прості і складні відсотки

Розглянемо схему однократного надання деякої суми Р в кредит на час t. За використання кредиту потрібно платити. Повернути потрібно S = Р + І, де / — плата за кредит. В найпростішому випадку вважають, що / = it, де і — процентна ставка.

Величина / вимірюється в грошових одиницях. Час t виміряєть­ся в роках, причому кількість років може бути не цілим числом, тоді використовуються долі року. Розмір процентної ставки і — грошових одиниць на рік.

Величина нарощеної суми визначається за формулою S = Р (1 + it). Відношення ■%■ називається коефіцієнтом нарощення.

Як же проводяться обчислення? Початкова сума Р задана, задана ставка процента і (причому потрібно слідкувати за коректністю розмі­ру: ставка повинна бути віднесеною до року), час потрібно визначити в долях року. Зауважимо, що день видачі позички і день погашення вва­жаються ОДНИМ ДНЄМ. ДОЛЯ року обчИСЛЮЄТЬСЯ За формуЛОЮ П = -JT, ДЄ

t — число днів позички; К — число днів у році (часова база).

Задача 1

Позичка в розмірі 1 млн. гривень видана 20 січня до 5 жовтнявключно під 18 % річних. Яку суму повинен заплатити боржник в кінці періоду?

Розв 'язування

Формулювання задачі потребує уточнення: в якому році ви­конувалася операція: у звичайному чи високосному. Проте функція ДОЛЯГОДА працює без урахування цієї обставини. Розглянемо три ва­ріанти (рис. 3.5).

Звернемося до фінансових функцій.

При використанні фінансових функцій потрібно враховувати зна­ки грошових сум, пам'ятаючи, з чиєї точки зору розглядається фінансова

Зацеркляний М. М., Мельников О. Ф. _^/*Зк^_

ІНФОРМАЦІЙНІ СИСТЕМИ І ТЕХНОЛОГІЇ У ФІНАНСОВО-КРЕДИТНИХ УСТАНОВАХ

Розділ З МОДЕЛІ І МЕТОДИ ФІНАНСОВО-ЕКОНОМІЧНИХ РОЗРАХУНКІВ

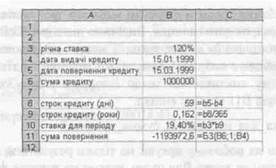
Рис. 3.6

Розв 'язування

Потрібно розрахувати майбутнє значення початкової суми. Скористаємося функцією БЗ {норма, число периодов, выплата, началь­ное значение, тип).

Перед тим, як скористатися цією функцією, потрібно виконати деякі розрахунки. Число періодів для простих відсотків, як уже було сказано, дорівнює 1. Відсотки є простими. Тому попередньо обчис­лимо процентну ставку за вказаний в умові задачі період. Початкові дані внесемо в комірки робочого аркушу в діапазон ВЗ.В6. В діапазоні АЗ:А6 розмістимо назви кожного параметра. Комірці ВИ призначимо грошовий формат (рис. 3.6).

Результат, як і треба було очікувати, виявився від'ємним.

З'ясуємо третій (пропущений) аргумент функції БЗ. Під виплатами тут розуміється проміжні рівні виплати на початку (тип = 1) чи в кінці (тип = 0) періоду. В даній задачі виплат немає.

Функція БЗ має коротку назву, яка легко запам'ятовується, і багато аргументів, порядок і призначення яких запам'ятати важко. Аби відра­зу розпочати роботу з другим діалоговим вікном Майстра функцій, по­ступають так: в комірку ВИ вводиться =БЗ (і натискується комбінація клавіш Ctrl+A. З'являється діалогове вікно з полями для введення ар­гументів.

При розв'язанні задач рекомендується заносити початкові дані в ко­мірки робочого аркуша, а не в формули; в сусідніх комірках — давати

*™ 113

A

ІНФОРМАЦІЙНІ СИСТЕМИ І ТЕХНОЛОГІЇ У ФІНАНСОВО-КРЕДИТНИХ УСТАНОВАХ ЩЩ

назви даних. Можна зробити формули набагато зрозумілішими, якщо замість адрес комірок дати їм назви. Виділимо діапазон АЗ:В10. В меню виконаємо Вставляння/Ім'я/Створити. З'являється діалогове вікно, в якому Excel пропонує вибрати імена з лівої колонки. Підтверджується цей вибір і знову викликається меню Вставляння/Ім'я/Застосувати. Формула в комірці ВИ прийме вигляд:

=БЗ (ставка_для_периода, 1„ суммакредита).

Розмістимо на робочому аркуші не тільки результати, а й форму­ли для розрахунку як текст. Для цього додамо на початок формул апо­строф — формули перетворюються в текст.

Приведемо формулу для розв'язування задачі, коли всі початкові дані розміщуються як аргументи у функцію БЗ. Хоча це є протиріччя «хорошому стилю» оформлення робочого аркушу, формула має само­стійний інтерес:

=БЗ(120%*("15/3/99"-"13/1/99")/365„1000000)

Зверніть увагу, що дати заключені в подвійні лапки. їх формат по­винен відповідати міжнародним налаштуванням Windows.

Перейдемо до схеми складних відсотків. У договорах вказуються річна ставка / і кількість нарахувань відсотків т на протязі року. Це озна­чає, що базовий період складає рік, поділений на т, а ставка складних відсотків для періоду дорівнює ііт. Формула для складних відсотків при­ймає вигляд:

Задача З

Позичка в 20 000 гривень дана на півтора року під ставку 28 % річ­них із щоквартальним нарахуванням. Визначити суму кінцевого платежу.

Розділ З МОДЕЛІ І МЕТОДИ ФІНАНСОВО-ЕКОНОМІЧНИХ РОЗРАХУНКІВ

Розе 'язування

Тут базовий період — квартал. Термін позички складає 6 періо­дів (4 квартали на рік, термін півтора року), за період нараховується 7 % = 28 %/4. Тоді формула, яка дає розв'язок задачі, має вигляд:

=БЗ(28%/4,4*1.5„20000).

Вона повертає результат — 30014.61.

Задача 4

Розрахувати майбутнє значення вкладу 1000 гривень через 0,1,2,3, 4, 5 років при річних ставках 10 %, 20 %,..., 50 %. Додаткові надходжен­ня і виплати відсутні.

Розв 'язування

В комірку В1 розмістимо величину початкового значення вкладу. В комірки B2:G2 розмістимо числа 0, 1,..., 5, в комірки АЗ:А7 величини 10, 20,..., 50 % (ці числа заносяться з використанням прийомів, які дозволя­ють генерувати арифметичні прогресії). Отже, потрібно табулювати функ-ціїо двох змінних (процентна ставка і кількість рокш), яка залежить від параметра — початкового вкладу. Вводиться в комірку ВЗ формула =БЗ ($АЗ,В$2„ — $В$1). Формула копіїоється в комірки інтервалу B3:G7.

Сталі ренти

Потік платежів, всі члени якого мають однакову величину R і роз­ділені рівними проміжками часу, називається сталою рентою. Один із можливих варіантів такого потоку {-Р, -R, -R, ..., -R, S}, тобто почат­ковий внесок Р і наступні виплати R дають в підсумку S. Якщо платежі виконуються в кінці періодів, то рента називається звичайною, або по-стнумерандо. Якщо платежі виконуються на початку періодів, то рента називається пренумерандо.

Формула, яку використовують функції Excel для розрахунків, має виглял'

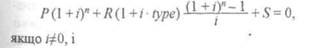
Зацеркляний М. М., Мельников О. Ф.

ІНФОРМАЦІЙНІ СИСТЕМИ І ТЕХНОЛОГІЇ У ФІНАНСОВО-КРЕДИТНИХ УСТАНОВАХ \

P + Rn + S=0,

якщо /-Q.

Тут Р — сучасне значення; S — майбутнє значення; R — періодична виплата; і — процентна ставка за період; п — кількість періодів, type — тип ренти, якщо type = 0 чи опущений, то рента постнумерандо (виплата в кінці періоду), якщо type = 1, то рента пренумерандо (виплата на по­чатку періоду).

Задача 5

На рахунок в банк вноситься сума 10000 гривеньь на протязі 10 ро­ків рівними долями в кінці кожного року. Річна ставка 4 %. Яка сума буде на рахунку через 10 років.

Розе 'язування

Платежі здійснюються в кінці періодів (рента постнумерандо), тому тип=0 (або його можна опустити). Формула = БЗ (4 %,10, — 10000) (аргумент начальное значение також необов'язковий, він опускається). Результат: 12006.11.

Якщо ж сума вноситься на початку року (рента пренумерандо), то формула приймає вигляд: =БЗ (4 %,10, -1000„1).

Задача 6

Вексель на 3 000 000 гривень із річною обліковою ставкою 10 % з дисконтуванням два рази на рік виданий на два роки. Знайти початкову суму, видану під цей вексель.

Розв 'язування

До цього часу використовувалася функція БЗ — майбутнє значен­ня. Тепер використаємо функцію ПЗ — приведене (сучасне) значення. Синтаксис функції ПЗ:

ПЗ (норма, количество_периодов, выплата, будущее_значение, тип).

В нашому випадку задача ускладнюється тим, що задана ставка дис­конта, а аргумент норма передбачає процентну ставку. Тому попередньо потрібно перерахувати дисконтну ставку у процентну. Нижче приведена

Розділ З МОДЕЛІ І МЕТОДИ ФІНАНСОВО-ЕКОНОМІЧНИХ РОЗРАХУНКІВ

таблиця, яка розв'язує по­ставлену задачу (рис. 3.7). У стовпчикові С розміщені формули стовпчика В, пе­ретворені в текст.

Має інтерес і така за­
дача: як, знаючи сучасне і
майбутнє значення, а також р_ис 3.7

періодичні рівні виплати, обчислити процентну ставку. Цю задачу розв'язує функція:

НОРМА (количествопериодов, выплаты, начальное_значение, тип, начальное_ приближение).

Функція повертає процентну ставку за один період. Начальное при­ближение за умовчуванням складає 10 %.

Задача 7

Нехай в борг на півтора року видана сума 2000 гривень із умовою повернення 3000 гривень. Знайти річну процентну ставку. Розв 'язування

=НОРМА (1.5„2000, -3000).

Результат: 31 %.

Найбільш складною частиною аналізу сталої ренти є визначення розміру виплат. Типова ситуація тут така. Кредитор видає на початку терміна деяку суму. Дебітор зобов'язується погасити заборгованість рів­ними долями. При цьому кожну виплату можна поділити на дві скла­дові — одна йде на погашення основної заборгованості, а інша — на процентні виплати.

Для нарахування виплат призначена функція:

ППЛАТ (ставка, количество_периодов, начальное_значение, буду-щеезначение, тип).

Зупинимося на передостанньому параметрі. Будущее значение — це баланс готівки, який потрібно досягти після останньої виплати. Якщо

Зацеркляний М. М., Мельников О. ф,

ІНФОРМАЦІЙНІ СИСТЕМИ І ТЕХНОЛОГІЇ У ФІНАНСОВО-КРЕДИТНИХ УСТАНОВАХ

Будущее значение опущено, то воно вважається рівним нулю (тобто за­боргованість погашена).

Для знаходження загальної суми, яка виплачується на протязі ін­тервалу виплат, потрібно помножити значення, що повертається функ­цією ГТПЛАТ, на кількість періодів.

Якщо потрібно дізнатися, яка частина виплат іде на погашення основної заборгованості, треба скористатися функцією:

ОСНПЛАТ (ставка, период, количество_периодов, начальное_зна-чение, будущее_значение, тип).

Другий параметр — период — це порядковий номер періоду, для якого виконується розрахунок. Цей номер належить інтервалу [1; коли­чество периодов] .

Частина виплат для обслуговування відсотків із основного боргу нараховується за допомогою функції:

ПЛПРОЦ (ставка, период, количество_периодов, начальное_зна-чение, будущее_значение, тип).

Задача 8

Банк видав довгостроковий кредит сумою 40 000 дол. на 5 років під 6 % річних. Погашення кредиту повинно проводитися рівними щоріч­ними виплатами в кінці кожного року, включаючи погашення основного боргу і процентні платежі. Нарахування відсотків виконується один раз на рік. Скласти план погашення позички.

Розв 'язування

Виплати складають сталу ренту постнумерандо. Результати обчис­лень приведені на рис. 3.8.

В діапазоні Е1.ЕЗ розміщуються початкові дані. В формулах, які здійснюють розв'язування задачі, використовуються іменовані посилан­ня на ці комірки, що дозволяє порівнювати різні варіанти, наприклад, що відбудеться при зміні процентної ставки. В рядках 6-Ю побудований план погашення по роках, а в рядкові 11 розміщені підсумкові цифри.

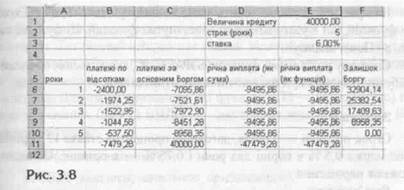
Нижче приведені формули із шостого рядка таблиці.

В6=ПЛПРОЦ (ставка, А6, срок, размер_ кредита)

С6=ОСНПЛАТ (ставка, А6, срок, размер_ кредита)

D6=C6+B6

Е6=ППЛАТ (ставка, срок, размер_ кредита)

F6=pa3Mep_ кредита+С6

Номер періода береться з першого стовпчика. При копіюванні фор­мул номер періода змінюється. В стовпчиках D і Е одержані, як і слід було чекати, однакові результати. В стовпчикові F формули, починаючи з сьомого рядка, інші: в комірці F7 записана формула =F6+C7. Вона копі­юється в інші комірки стовпчика. Відповідно налаштовується адреса. В комірці ВИ розмішується формула =СУММ (В6:В10). Аналогічні фор­мули розміщені в інших комірках 11-го рядка.

Із поданої на рис. 3.8 таблиці неважко бачити, що при погашенні бор­гу рівними платежами залишок боргу з кожною виплатою зменшується, отже, зменшуються і процентні виплати. В результаті зростає від періоду до періоду величина платежу, який іде на погашення основного боргу.