Классификационные признаки систем массового обслуживания. 5 страница

На второй год с момента ввода:

на шахте 1 добыча угля К2 и СС выше по обоим вариантам на 10% при росте затрат на 10%;

на шахте 2 по первому варианту добыча К2 больше на 10%, а добычаСС меньше на 10% при неизменных затратах, по второ­му варианту добыча К2 меньше на 10%, а добыча СС больше на 10% при неизменных затратах;

на шахте 3 по обоим вариантам объем добычи и затраты те же, что и для первого года.

Любая шахта может быть введена как в первый, так и во вто­рой год планового периода. Введенные мощности продолжают ис­пользоваться в последующие периоды времени.

Составьте план ввода мощностей по добыче угля, обеспечива­ющий выполнение плановых заданий с минимальными затратами.

Вопросы:

1. Каковы минимальные затраты?

2. Следует ли использовать вариант 1 развития шахты 2?

Задача 7. Для реконструкции машиностроительного предпри­ятия было представлено 10 проектов, каждый из которых харак­теризуется четырьмя агрегированными показателями: затратами труда, энергии, материалов, денежных средств, а также ежегод­ной прибылью в случае реализации проекта. Соответствующие данные и объем имеющихся ресурсов приведены в таблице:

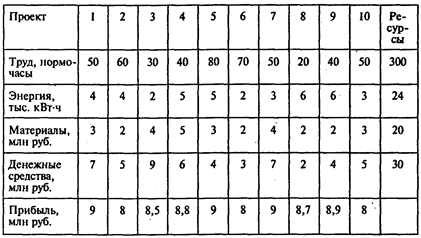
При выборе проектов необходимо учесть ряд ограничений тех­нологического характера:

1) одновременно может быть реализовано не более семи про­ектов;

2) проекты 5 и 8 исключают друг друга;

3) проект 1 может быть реализован лишь при условии реали­зации проекта 2;

4) проект 4 может быть реализован лишь при условии реали­зации хотя бы одного из двух проектов: либо проекта 3, либо про­екта 10.

Вопросы:

1. Какова максимальная прибыль?

2. Следуетли реализовывать проект 3?

Задача 8. Имеются одинаковые заготовки, которые могут быть раскроены тремя способами и из которых могут быть получены не менее 10 деталей первого типоразмера, не менее 8 деталей вто­рого типоразмера и не менее 10 деталей третьего типоразмера.

Способы раскроя представлены в следующей матрице:

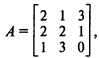
где а_ij — количество деталей типоразмера i, получаемое из одной заготовки путем ее раскроя способом j.

Количество заготовок, раскраиваемых каждым способом, долж­но быть целым и не превышать 4. Отходы от одной заготовки для каждого из способов раскроя составляют соответственно 4,5 и 5 см.

Выполните раскрой с минимальными суммарными отходами.

Вопросы:

1. Сколько заготовок должно быть раскроено вторым способом?

2. Чему равны минимальные суммарные отходы?

Ответы и решения

Ответы на вопросы: 1— 4, 2 — 4, 3— 5,4 — 4.

Задача 1. Решение.

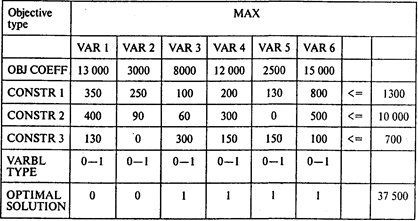
Ответы: 1. 37 500 тыс. руб. 2. Четыре мероприятия.

Задача 2. Решение.

Если преследуется цель минимизации количества дополнительных работ, то модель будет иметь вид (затраты со знаком минус):

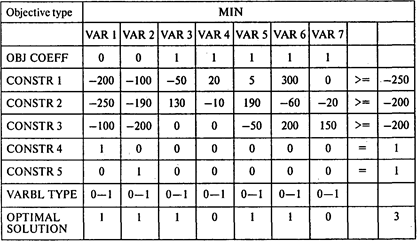
Ответ: Три мероприятия.

Задача 3. Решение.

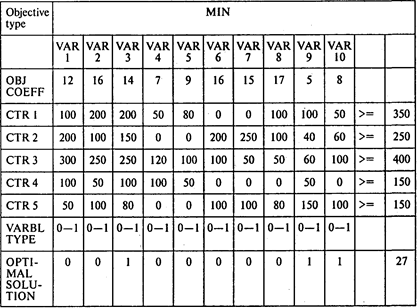
Ответы: 1. 27 млн руб. 2. Нет, не следует.

Задача 4. Решение.

Пусть VAR 1 равен единице, если первый сорт нефти находится в первом ре­зервуаре, и нулю в противном случае и т.д. Введем следующие обозначения:

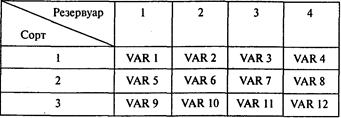
При минимизации затрат на хранение полученное решение будет иметь вид

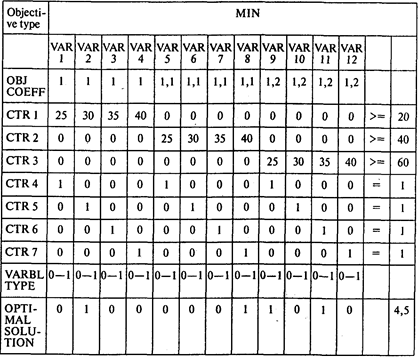
Ответы: 1. Четыре резервуара. 2. Первого сорта.

Задача 5. Решение.

Производственное объединение выпускает три продукта:

1) кабель силовой;

2) провод для осветительных установок;

3) провод обмоточный.

На каждый год трехлетнего периода установлено задание по объему производ­ства каждого из этих продуктов. Таким образом, в модель следует ввести девять ограничений по объему выпуска.

Производственное задание может быть выполнено, если будут реализованы наилучшие варианты развития всех предприятий, входящих в объединение. Пер­вый завод, по условию, имеет три варианта развития, второй — два, третий — один. Всего вариантов шесть, но каждый завод должен выбрать только один из своих вариантов. Таким образом, в модели следует учесть еще три ограничения.

В результате получаем модель с двенадцатью ограничениями и шестью пере­менными.

Целевая функция —минимизация затрат на выполнение задания по объему производства.

В следующей таблице представлены структурные модели и решение задачи:

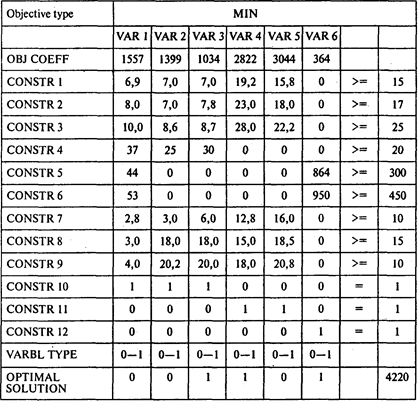
Ответы: 1. 4220 млн руб. 2. Да, следует.

Задача 6. Решение.

Обозначения:

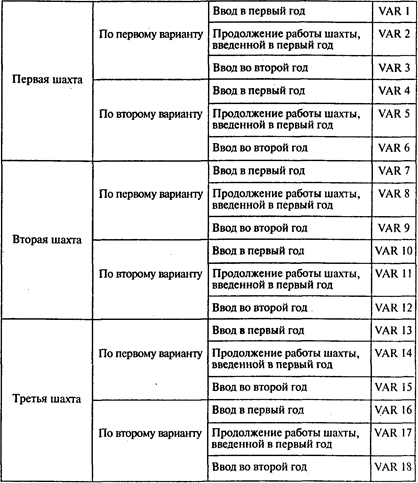
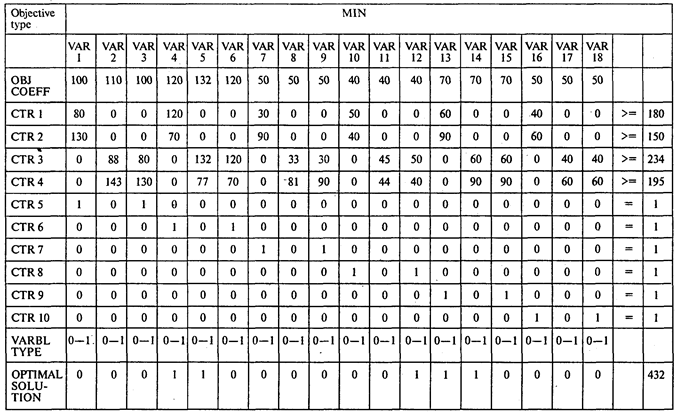
В таблице на с. 407 представлены структура модели и решение задачи.

Ответы: 1. 432 тыс. руб. 2. Нет, не следует.

Задача 7. Решение.

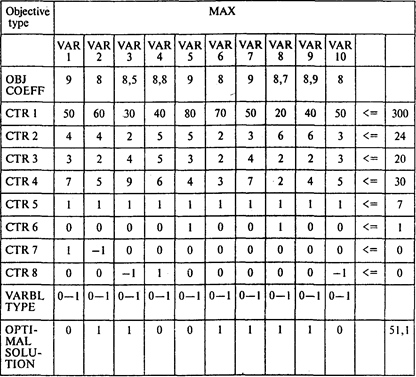
Ответы: 1. 51,1 млн руб. 2. Да, следует.

Задача 8. Решение.

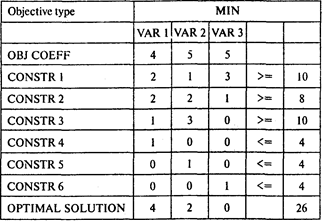
Ответы: 1. Две заготовки, 2. 26см.

Глава 16. Основы теории принятия решений

Цели

Человеку постоянно приходится принимать решения. Так, прежде чем выйти из дому, вы задумываетесь над тем, взять ли зонт. Конечно, не хотелось бы носить его с собой в хорошую по­году. Но в дождливый день зонт будет весьма кстати. Так брать или не брать зонт?

Ответить на этот вопрос несложно, если точно знать, какая будет погода. Если с утра идет дождь, большинство людей возьмет зонты. Хотя, возможно, не все. Некоторые закаленные люди ско­рее предпочтут промокнуть, лишь бы не носить весь день с со­бой зонт. Последствия отсутствия зонта в плохую погоду оцени­ваются каждым человеком по-разному. Эти оценки влияют на ре­шение.

Сложнее принять решение, если отсутствует достоверная ин­формация о том, какая ожидается погода. Нельзя полностью до­верять прогнозу. Он никогда не бывает абсолютно точным. Еще сложнее принять решение, если вы прогноза не знаете.

Методы принятия решений в условиях отсутствия достоверной информации о возможных последствиях изучаются теорией риска. Эта теория имеет широкую сферу приложений в экономи­ке. Одно из наиболее важных — выбор инвестиционных проектов.

После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь определять и использовать для экономи­ческого анализа следующие понятия:

• альтернатива;

• состояние среды;

• таблица решений;

• дерево решений;

• критерий безразличия;

• критерий оптимизма;

• критерий пессимизма;

• ожидаемая стоимостная оценка альтернативы;

• ожидаемая ценность достоверной информации.

Кроме того, вы научитесь принимать решения в условиях не­определенности, определенности и в условиях риска.

Модели

Теория принятия решений — это аналитический подход к вы­бору наилучшей альтернативы или последовательности действий. В теории принятия решений существуют три основных уровня классификации. Они зависят от степени определенности возмож­ных исходов или последствий, с которыми сталкивается лицо, принимающее решения (ЛПР).

Соответственно существуют три типа моделей:

1. Принятие решений в условиях определенности — ЛПР точно знает последствия и исходы любой альтернативы или выбора ре­шения. Например, ЛПР с полной определенностью знает, что вклад 100 тыс. руб. на текущий счет приведет к увеличению ба­ланса этого счета на 100 тыс. руб.

2. Принятие решений в условиях риска — ЛПР знает вероятнос­ти наступления исходов или последствий для каждого решения. Мы можем не знать того, что завтра будет дождь, но мы можем знать, что вероятность дождя 0,3.

3. Принятие решений в условиях неопределенности — ЛПР не знает вероятностей наступления исходов для каждого решения. Например, вероятность того, что весь тираж этой книги будет реализован за год, авторам неизвестна.

Если имеет место полная неопределенность в отношении воз­можности реализации состояний среды (т.е. мы не можем даже приблизительно указать вероятности наступления каждого воз­можного исхода), то обстоятельства, с которыми мы имеем дело при выборе решения, можно представить как вид стратегической игры, в которой один игрок — ЛПР, а другой — некая объектив­ная действительность, называемая природой. Условия такой игры обычно представляются следующей таблицей решений, в которой строки А₁, А₂, ..., А_m, соответствуют стратегиям ЛПР, а столбцы N₁, N₂,..., N_n — стратегиям природы (a_ij — выигрыш ЛПР, соот­ветствующий каждой паре A_i, N_j):

В рассматриваемой ситуации при выборе из множества {А₁, А₂, ..., А_m} наилучшего решения обычно используют следу­ющие критерии:

1. Максимаксный критерий, или критерий крайнего оптимизма — определяет альтернативу, которая максимизирует максималь­ный результат для каждой альтернативы, т.е. ЛПР выбирает стра­тегию sq, которой соответствует

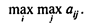
2. Максиминный критерий Вальда, или критерий крайнего пес­симизма — определяет альтернативу, которая максимизирует ми­нимальный результат для каждой альтернативы, т.е. ЛПР выби­рает стратегию i₀, которой соответствует

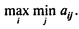
3. Критерий минимаксного риска Сэвиджа. Согласно этому кри­терию выбирается стратегия, при которой величина риска r_ij в наихудших условиях минимальна, т.е. равна

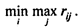
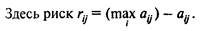
4. Критерий оптимизма-пессимизма Гурвица — рекомендует при выборе решения не руководствоваться ни крайним пессимизмом, ни крайним оптимизмом. Согласно этому критерию стратегия выбирается из условия

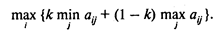
Значение коэффициента пессимизма k выбирается между ну­лем и единицей. При k = 1 критерий Гурвица превращается в критерий Вальда, при k > 0 — в критерий крайнего оптимизма.

5. Критерий безразличия. В условиях полной неопределеннос­ти предполагается, что все возможные состояния среды (приро­ды) равновероятны. Этот критерий выявляет альтернативу с мак­симальным средним результатом, т.е.

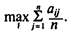
Если известна таблица решений с оценками условий и вероят­ностями реализации для всех состояний среды, можно определить ожидаемую стоимостную оценку ЕМV для каждой альтернативы. Один из наиболее распространенных критериев выбора альтерна­тивы — максимальная ЕМV.

Для каждой альтернативы ожидаемая стоимостная оценка ЕМV есть сумма всевозможных оценок условий (выигрышей) для этой альтернативы, умноженных на вероятности реализации этих вы­игрышей:

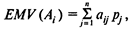
где a_ij — выигрыш ЛПР при выборе альтернативы i и реализации состояния среды j, j =1,..., n;

р_j — вероятность наступления состояния среды j.

Ожидаемой ценностью достоверной информации EVPI назовем разность между выигрышем в условиях определенности и выиг­рышем в условиях риска.

Для того чтобы определить EVPI, вначале необходимо рассчи­тать математическое ожидание в условиях определенности, кото­рое равно ожидаемому (или среднему) доходу в случае, когда мы имеем достоверную информацию перед тем, как принять реше­ние.

Ожидаемый выигрыш в условиях достоверной информации определяется как

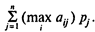
Тогда

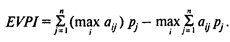
Таблицу решений удобно использовать при анализе задач, име­ющих одно множество альтернативных решений и одно множе­ство состояний среды. Многие задачи, однако, содержат последо­вательности решений и состояний среды. Если имеют место два (или более) последовательных решения и последующее решение основывается на исходе предыдущего, более предпочтителен под­ход, основанный на построении дерева решений.

Дерево решений — это графическое изображение процесса ре­шений, в котором отражены альтернативные решения, состояния среды, а также соответствующие вероятности и выигрыши для любых комбинаций альтернатив и состояний среды.

Анализ задач с помощью дерева решений включает пять этапов:

1) формулировка задачи;

2) построение дерева решений;

3) оценка вероятностей состояний среды;

4) установление выигрышей для каждой возможной комбина­ции альтернатив и состояний среды;

5) решение задачи путем расчета ожидаемой стоимостной оцен­ки ЕМУ для каждой вершины состояния среды.

Примеры

Пример 1. Выбор альтернативы.

Компания «Буренка» изучает возможность производства и сбы­та навесов для хранения кормов. Проект может основываться на большой или малой производственной базе. Рынок для реализа­ции навесов может быть благоприятным или неблагоприятным.

Василий Бычков — менеджер компании — учитывает возмож­ность вообще не производить эти навесы. При благоприятной рыночной ситуации большое производство позволило бы Бычко­ву получить чистую прибыль 200 тыс. руб. Если рынок окажется неблагоприятным, то при большом производстве компания поне­сет убытки в размере 180 тыс. руб. Малое производство дает 100 тыс. руб. прибыли при благоприятной рыночной ситуации и 20 тыс. руб. убытков при неблагоприятной.

Вопрос: Какую альтернативу следует выбрать?

Решение. Применим перечисленные выше критерии. Соста­вим таблицу решений (k = 0,75):

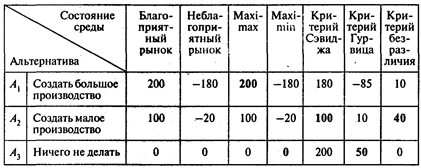
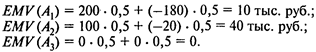
Решение в этом случае совпадает с решением, полученным в примере 1 по критерию безразличия.

Ответ: Следует выбрать альтернативу А₂

Пример 3. Принятие решения об использовании дополнительной информации.

Предположим, что менеджер компании «Буренка» (см. при­мер 1) связался с фирмой, занимающейся исследованием рынка, которая предложила ему помощь в принятии решения о том, сто­ит ли создавать производство навесов для хранения кормов. Ис­следователи рынка утверждают, что их анализ позволит установить с полной определенностью, будет ли рынок благоприятным для данного продукта. Другими словами, условия для компании «Бу­ренка» меняются от принятия решений в условиях риска к при­нятию решений в условиях определенности. Эта информация мо­жет предостеречь Бычкова от очень дорогостоящей ошибки. Фир­ма, занимающаяся исследованием рынка, хотела бы получить за эту информацию 65 тыс. руб.

Вопрос: Следует ли воспользоваться услугами указанной фир­мы? Даже если результаты исследования являются со­вершенно точными, оправдана ли плата 65 тыс. руб.?

Решение. 1. Лучший исход для состояния среды «благоприятный рынок» — «создать большое производство» с выигрышем 200 тыс. руб., а для состояния среды «неблагоприятный рынок» — «ничего не делать» с выигрышем 0. Ожидаемая стоимостная оценка в усло­виях определенности равна 200 • 0,5 + 0 • 0,5 = 100 тыс. руб.

Итак, если бы мы располагали достоверной информацией, мы ожидали бы получить в среднем 100 тыс. руб.

2. Максимум ЕМУ равен 40 тыс. руб. Это размер ожидаемого дохода без достоверной информации.

3. EVPI= Ожидаемая стоимостная оценка в условиях опреде­ленности — Максимум ЕМV = 100 — 40 = 60 тыс. руб.

Итак, Бычкову следовало бы платить за достоверную инфор­мацию не более 60 тыс. руб. Конечно, такой вывод основывается на предположении, что вероятность реализации каждого состояния среды равна 0,5.

Ответ: Приобретать достоверную информацию не следует.

Пример 4. Взаимосвязанные решения.

Предположим, что Бычкову (см. пример 1) надо принять два решения, причем второе решение зависит от исхода первого. Прежде чем создать новое производство. Бычков намерен зака­зать исследование рынка и заплатить за него 10 тыс. руб. Резуль­таты этого исследования могли бы помочь решить вопрос о том, следует ли создавать большое производство, малое производство или не делать ничего. Бычков понимает, что такое обследование рынка не может дать достоверную информацию, но может тем не менее оказаться полезным.

Вопрос: Следует ли проводить обследование рынка?

Решение. На рис. 1 показаны возможные состояния среды и решения, а также вероятности различных результатов обследова­ния и вероятности наступления различных состояний среды. (Прямоугольники используются для обозначения вершин приня­тия решений, кружочки обозначают неконтролируемые события — наступление состояний среды.)

Дерево решений Бычкова с рассчитанными EMV представле­но на рис. 2. Короткими параллельными линиями отсекается та ветвь, которая оказывается менее благоприятной по сравнению с другими и может быть отброшена.

Ожидаемая стоимостная оценка наилучшего решения в случае, если будет заказано обследование рынка, составляет 49,2 тыс. руб., без обследования она составляет 40 тыс. руб.

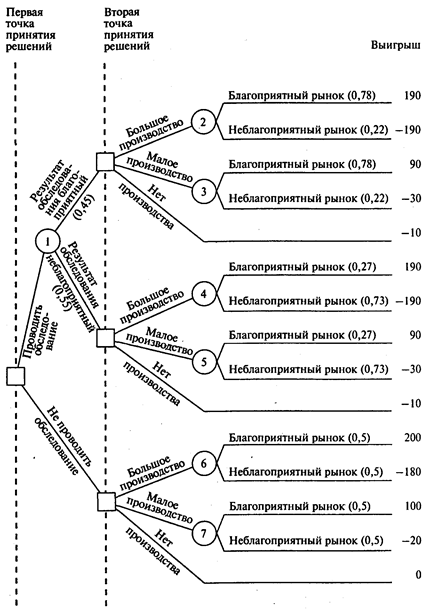
Рис. 1

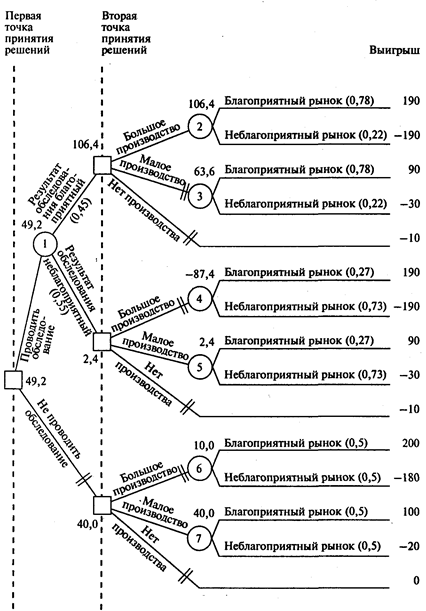
Рис.2

Ответ: Да, следует заказывать обследование рынка. Если ре­зультат обследования будет благоприятным, следует со­здавать большое производство, если неблагоприятным — малое.

Вопросы

Вопрос 1. В теории принятия решении ситуация, которую не может контролировать лицо, принимающее решение, называется:

1) деревом решений;

2) состоянием среды;

3) решением в условиях неопределенности;

4) альтернативой;

5) таблицей решений.

Вопрос 2. Укажите правильное соответствие названий крите­риев принятия решений в условиях неопределенности:

1) minmax « «критерий оптимизма»;

2) maxmin « «критерий пессимизма»;

3) minmin « «критерий пессимизма»;

4) maxmin « «критерий безразличия»;

5) maxmax « «критерий безразличия».

Вопрос 3. В задаче принятия решений рассматривается одно множество состояний среды и одно множество решений. Если вероятность наступления одного из состояний среды равна еди­нице, то решение принимается в условиях:

1) частичной неопределенности;

2) неопределенности;

3) определенности;

4) безразличия;

5)риска.

Вопрос 4. Можно сделать одно из следующих приобретений: квартира, земельный участок, речной катер, авторемонтная мас­терская или небольшое кафе. В случае если обстоятельства сло­жатся благоприятно, прибыль составит соответственно 22, 12, 17, 25 или 30 тыс. руб. В случае неблагоприятного стечения обстоя­тельств покупка квартиры или земельного участка принесет при­быль соответственно 7 или 9 тыс. руб., а покупка катера, авторе­монтной мастерской или кафе — убытки соответственно 5, 11 или 13 тыс. руб.

Благоприятное и неблагоприятное стечение обстоятельств рав­новероятно. В этом случае достоверная информация о состоянии среды оценивается величиной:

1) 15,5 тыс. руб.;

2) 10 тыс. руб.;

3) 8 тыс. руб.;

4) 5 тыс. руб.;

5) 2 тыс. руб.

Вопрос 5. Модель принятия решений в условиях риска отно­сится к классу моделей:

1) имитационных;

2) статистических;

3)алгебраических;

4) управления запасами;

5) математического программирования.

Вопрос 6. Пусть в качестве критерия принятия решения в условиях риска используется ожидаемая стоимостная оценка аль­тернативы ЕМV. Вероятность того, что фактический выигрыш будет равен значению ЕМV:

1) высока;

2) зависит от числа альтернатив;

3) мала;

4) зависит от числа состояний среды;

5) ничто из вышеуказанного не является верным.

Задачи

Задача 1. Лукерья Скальпель — администратор больницы в Почаеве. Она решает, следует ли сделать к больнице большую при­стройку, маленькую пристройку или не делать пристройки вооб­ще. Если население Почаева будет продолжать расти, то большая пристройка могла бы приносить ежегодно прибыль в 150 тыс. руб. Если будет сделана маленькая пристройка, то она может прино­сить больнице 60 тыс. руб. прибыли ежегодно при условии, что население будет увеличиваться. Если население Почаева не будет увеличиваться, то сооружение большой пристройки принесет больнице убыток в 85 тыс. руб., а маленькой — в 45 тыс. руб. К со­жалению, у Лукерьи нет информации о том, как будет изменять­ся численность населения Почаева.

Постройте таблицу решений. Определите наилучшую альтер­нативу, используя критерий безразличия.

Вопросы:

1. Чему равно значение ЕМV для наилучшей альтернативы?

2. Получена дополнительная информация: вероятность роста населения равна 0,6, вероятность того, что его численность останется неизменной, — 0,4. Определите наилучшее реше­ние, используя критерий максимизации ожидаемой стоимост­ной оценки. Чему равно значение ЕМV для наилучшей альтернативы при наличии дополнительной информации?

3. Какова ожидаемая ценность дополнительной информации?

Задача 2. Тамара Пончик предполагает построить ресторан не­далеко от университетского общежития. Один из возможных ва­риантов — предусмотреть в нем пивной бар. Другой вариант не связан с продажей пива. В обоих случаях Тамара оценивает свои шансы на успех как 0,6 и на неудачу как 0,4. Предварительные обсуждения показывают, что план, связанный с продажей пива, может принести 325 тыс. руб. прибыли. Без продажи пива можно заработать 250 тыс. руб. Потери в случае открытия ресторана с ба­ром составят 70 тыс. руб., в случае ресторана без бара — 20 тыс. руб.

Выберите альтернативу для Тамары Пончик на основе средней стоимостной оценки в качестве критерия.

Вопросы:

1. Следует ли реализовать план, предусматривающий продажу пива?

2. Чему равно значение ЕМV для наилучшей альтернативы?

Задача 3. «Фотоколор» — небольшой магазин, торгующий хи­мическими реактивами, которые используются некоторыми фо­тостудиями при обработке пленки. Один из продуктов, который предлагает «Фотоколор», — фиксаж ВС-6. Адам Полутонов, ди­ректор магазина, продает в течение месяца 11, 12 или 13 ящиков ВС-6. От продажи каждого ящика фирма получает 35 тыс. руб. прибыли. Фиксаж ВС-6, как и многие фотореактивы, имеет ма­лый срок годности. Поэтому, если ящик не продан к концу месяца, Адам должен его уничтожить. Так как каждый ящик обходит­ся магазину в 56 тыс. руб., он теряет их в случае, если ящик не продан к концу месяца. Вероятность продать 11, 12 или 13 ящи­ков в течение месяца равна соответственно 0,45; 0,35 и 0,2.

Вопросы:

1. Сколько ящиков закупать фирме для продажи ежемесячно?

2. Какова ожидаемая стоимостная оценка этого решения?

3. Сколько ящиков следовало бы закупать, если бы Адам мог достать фиксаж ВС-6 с добавкой, которая значительно про­длевает срок его годности?

Задача 4. Компания «Молодой сыр» — небольшой производи­тель различных продуктов из сыра. Один из продуктов — сырная паста — продается в розницу. Вадим Ароматов, менеджер компа­нии, должен решить, сколько ящиков сырной пасты следует про­изводить в течение месяца. Вероятность того, что спрос на сыр­ную пасту в течение месяца будет 6, 7, 8 или 9 ящиков, равна со­ответственно 0,1;-0,3; 0,5; 0,1. Затраты на производство одного ящика пасты составляют 45 тыс. руб. Ароматов продает каждый ящик по цене 95 тыс. руб. Если сырная паста не продается в те­чение месяца, то она портится и компания не получает дохода.

Вопросы:

1. Сколько ящиков следует производить в течение месяца?

2. Какова ожидаемая стоимостная оценка этого решения?

Задача 5. Дмитрий Мухин не знает, что ему предпринять. Он может открыть в своей аптеке или большую, или маленькую сек­цию проката видеокассет. Мухин может получить дополнитель­ную информацию о том, будет рынок видеопроката благоприят­ным или нет. Эта информация обойдется ему в 3 млн руб. Дмит­рий считает, что эта информация окажется благоприятной с вероятностью 0,5. Если рынок будет благоприятным, то большая секция проката принесет прибыль 15 млн руб., а маленькая — 5 млн руб. При неблагоприятном рынке Мухин потеряет 20 млн руб. в случае, если он откроет большую секцию, и 10 млн руб. в случае, если маленькую. Не имея дополнительной информации, Дмитрий оценивает вероятность благоприятного рынка как 0,7. Положи­тельный результат обследования гарантирует благоприятный ры­нок с вероятностью 0,9. При отрицательном результате рынок может оказаться благоприятным с вероятностью 0,4.

Вопросы:

1. Следует ли получить дополнительную информацию?

2. Следует лиоткрыть большую секцию?

3. Какова ожидаемая стоимостная оценка наилучшего решения?

Задача 6. Павел Спицын провел анализ, связанный с откры­тием магазина велосипедов. Если он откроет большой магазин, то при благоприятном рынке получит 60 млн руб., при неблагопри­ятном — понесет убытки 40 млн руб. Маленький магазин принесет ему 30 млн руб. прибыли при благоприятном рынке и 10 млн руб. убытков — при неблагоприятном. Возможность бла­гоприятного и неблагоприятного рынка он оценивает одинаково. Исследование рынка, которое может провести профессор, обой­дется Спицыну в 5 млн руб. Профессор считает, что с вероятнос­тью 0,6 результат исследования рынка окажется благоприятным. В то же время при положительном заключении рынок окажется благоприятным с вероятностью 0,9. При отрицательном заключе­нии рынок может оказаться благоприятным с вероятностью 0,12.

Используйте дерево решений для того, чтобы помочь Павлу сделать правильный выбор.

Вопросы:

1. Следует ли заказать проведение обследования рынка?

2. Следует ли открыть большой магазин?

3. Какова ожидаемая стоимостная оценка наилучшего ре­шения?

Задача 7. Компания «Луч» получает переключатели у двух по­ставщиков. Качество переключателей охарактеризовано в следу­ющей таблице:

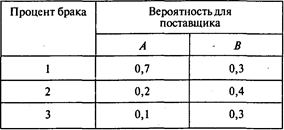
Так, 1% всех переключателей, поставляемых поставщиком А, с вероятностью 0,7 окажется бракованным. Так как каждый заказ компании составляет 10 000 переключателей, это означает, что с вероятностью 0,7 они получат от этого поставщика 100 бракован­ных переключателей. Бракованный переключатель можно отремон­тировать за 0,5 тыс. руб. Качество у поставщика В ниже, поэтому он уступает партию в 10 000 переключателей на 37 тыс. руб. дешев­ле, чем поставщик А.

Вопросы:

1. Какого поставщика следует выбрать компании?

2. Какова ожидаемая стоимостная оценка наилучшего решения?

Задача 8. Ивану Хлоркину, главному инженеру компании «Бе­лый каучук», надо решить, монтировать или нет новую производ­ственную линию с использованием последних технологий. Если новая линия будет работать безотказно, компания получит при­быль 200 млн руб. Если линия откажет, компания может потерять 150 млн руб. По оценкам Хлоркина, в 60% случаев новая линия откажет. Можно создать экспериментальную установку, а затем уже решать, монтировать или нет новую линию. Эксперимент обойдется в 10 млн руб. Иван считает, что в 50% случаев экспе­риментальная установка будет работать. Если она будет работать, то в 90% случаев производственная линия (если ее смонтировать) также будет работать. Если установка не будет работать, то есть только 20% шансов, что линия будет работать.