Классификационные признаки систем массового обслуживания. 3 страница
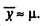
Оценка дисперсии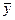 
(если временной ряд не является автокоррелированным) имеет вид
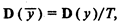
где D(у) — дисперсия случайной величины у.
Для оценки качества результатов, полученных методом Монте-Карло при неизвестной дисперсии наблюдаемой случайной величины, предположим, что Z — характеристика, которая должна быть определена (вероятность события, математическое ожидание, дисперсия и т.п.), a x — ее значение, уточняемое по мере накопления данных, остающееся случайным вследствие ограниченности числа T проведенных наблюдений. В этих условиях можно говорить о вероятности p(|Z – x| < e) по отношению к интересующей нас характеристике. Величина |Z – e| представляет собой погрешность в оценке Z, a e — некоторый допустимый ее предел.
Из неравенства Чебышёва следует
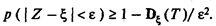
Из этого неравенства следует
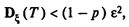
откуда при заданных р и e и при известной зависимости De (Т)можно найти предельно необходимое Т.
Известно, что истинная дисперсия выборочного распределения для расчетного среднего обратно пропорциональна суммарному числу наблюдений Т, т.е.
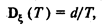
где d не зависит от Т.
В начале имитационного процесса требуемое число наблюдений определить обычно не удается, поскольку d неизвестно. Поэтому, как правило, эксперимент проводят в два этапа.
На первом этапе число испытаний выбирается относительно небольшим, в результате определяется величина d. После этого можно уже определить, сколько дополнительных наблюдений необходимо, чтобы была достигнута требуемая точность.
Предельное число наблюдений Т0 определяется формулой T0 = d/[(1 – p)e2].
При любом числе наблюдений больше Т0 обеспечивается требуемая точность.
Примеры
Пример 1. Моделирование объема спроса на автомашины.
Наблюдения за объемом продаж автомобилей в салоне «ЛОГОВАЗ» в течение 200 дней показали, что величина спроса изменяется от 0 до 5 автомобилей в день. Частота реализации значений стохастической переменной приведена во втором столбце таблицы:
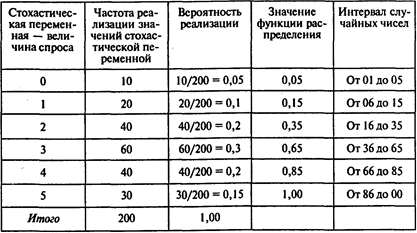
Постройте модель, позволяющую имитировать значение величины спроса.
Решение. Построим функцию распределения величины спроса и интервалы случайных чисел для значений стохастической переменной. Соответствующие значения указаны в четвертом и пятом столбцах вышеприведенной таблицы.
Сымитируем спрос на автомашины в салоне «ЛОГОВАЗ» в течение 10 последующих дней (случайные числа из таблицы случайных чисел (Приложение 2) выбираем, начиная из верхнего левого угла и двигаясь вниз в первом столбце):
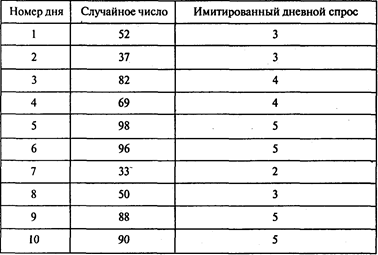
В результате получаем: 39 — спрос за 10 дней; 39/10 = 3,9 — средний ежедневный спрос.
Оценка 3,9 средней величины спроса, полученная в результате имитационного эксперимента, существенно отличается от значения 2,95 — математического ожидания этой случайной величины. Однако эта разница уменьшается с ростом числа испытаний.
Пример 2. Моделирование очереди на разгрузку.
Груженые баржи, отправляемые вниз по Волге из индустриальных центров, достигают Астрахани. Число барж, ежедневно входящих в док, колеблется от 0 до 5. Вероятность прихода 0, 1,..., 5 барж показана в таблице:
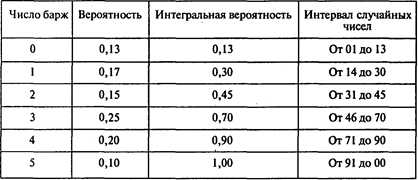
В этой же таблице указаны интегральные вероятности и соответствующие интервалы случайных чисел для каждого возможного значения.
Аналогичная информация дана о числе разгружаемых барж:
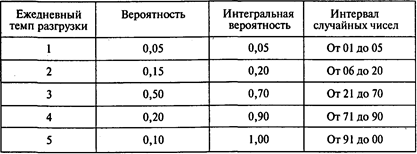
Постройте модель, позволяющую имитировать очередь на разгрузку.
Решение. Проведем эксперимент, имитирующий очередь на разгрузку барж в порту Астрахани:
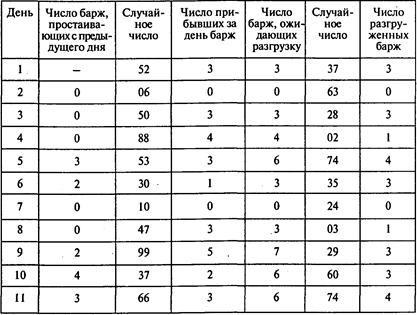
Окончание таблицы
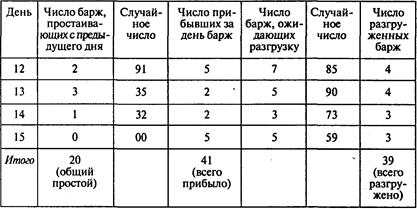
В результате эксперимента получены:
оценка среднего числа барж, простаивающих в течение суток, равная 20/15;
оценка среднего числа барж, прибывающих в течение суток, равная 41/15;
оценка среднего числа барж, разгруженных в течение суток, равная 39/15.
Пример 3. Имитация стратегии резервирования.
Магазин электрооборудования продает электрические дрели. В течение 300 дней директор магазина Проводков регистрировал дневной спрос на дрели. Распределение вероятностей величины спроса показано в таблице:
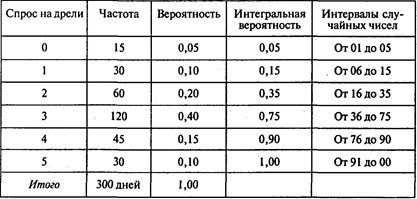
Когда Проводков делает заказ, чтобы возобновить свои запасы электрических дрелей, его выполнение происходит с лагом в 1, 2 или 3 дня. Это означает, что время восстановления запаса подчиняется вероятностному распределению. В следующей таблице указаны сроки, вероятности сроков выполнения заказов и интервалы случайных чисел, которые удалось определить на основе информации о 50 заказах:
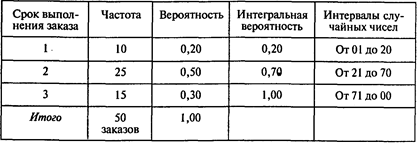
Стратегия резервирования, которую хочет имитировать Проводков, — делать заказ в объеме 10 дрелей при запасе на складе 5 шт. Проводков оценил, что каждый заказ на дрели обходится ему в 10 руб., хранение каждой дрели — в 5 руб. в день, одна упущенная продажа — в 80 руб. Цель эксперимента — оценить величину средних ежедневных затрат для этой стратегии управления запасами.
Решение. Реализуется четырехшаговый процесс имитации:
1. Каждый имитируемый день начинается с проверки, поступил ли сделанный заказ. Если заказ выполнен, то текущий запас увеличивается на величину заказа (в данном случае — на 10 единиц).
2. Путем выбора случайного числа генерируется дневной спрос для соответствующего распределения вероятностей.
3. Рассчитывается итоговый запас, равный исходному запасу за вычетом величины спроса. Если запас недостаточен для удовлетворения дневного спроса, спрос удовлетворяется, насколько это возможно. Фиксируется число нереализованных продаж.
4. Определяется, снизился ли запас до точки восстановления (в примере — 5 единиц). Если да, причем не ожидается поступления заказа, сделанного ранее, то делается заказ.
Первый эксперимент Проводкова (объем заказа — 10 шт., точка восстановления запаса — 5 шт.; СЧ — случайное число):
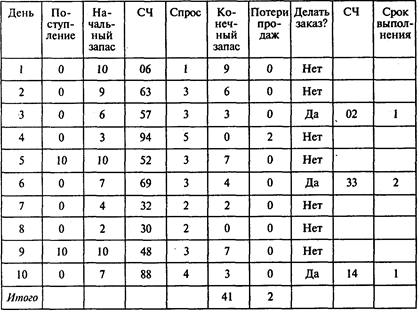
Результат имитационного эксперимента:
конечный суммарный запас — 41 единица;
средний конечный запас 41/10 =4,1 единицы;
число упущенных продаж — 2;
среднее число упущенных продаж 2/10 = 0,2 шт. в день;
среднее число заказов 3/10 = 0,3 заказа в день.
Определим три составляющие затрат:
Ежедневные затраты на заказы = Затраты на один заказ х Среднее число заказов в день = 10 • 0,3 = 3 руб.
Ежедневные затраты на хранение = Затраты на хранение одной единицы в течение дня х Средняя величина конечного запаса = 5 • 4,1 = 20,5 руб.
Ежедневные упущенные продажи = Прибыль от упущенной продажи х Среднее число упущенных продаж в день = 80 • 0,2 = 16 руб.
Таким образом,
Общие ежедневные затраты = Затраты на заказы + Затраты на хранение + Упущенные продажи = 3 + 20,5 + 16 = 39,5 руб.
Вопросы
Вопрос 1. Для моделирования случайной величины Х в имитационной модели используется метод Монте-Карло. Случайная величина X может принимать значения 2, 3 и 4. При 200 наблюдениях эти значения реализуются с частотами 42, 88 и 70 соответственно. Определите интервал случайных чисел для значения Х = 3.
Варианты ответов:
1) от 1 до 42;
2) от 43 до 88;
3) от 22 до 65;
4) от 43 до 65;
5) от 66 до 100.
Вопрос 2. Метод имитации называется методом Монте-Карло, если:
1) для проведения вычислений используется компьютер;
2) метод позволяет сэкономить деньги;
3) метод использует значения вероятностей;
4) все вышеуказанное является верным;
5) ничто из вышеуказанного не является верным.
Вопрос 3. Длина интервала случайных чисел:
1) зависит от значения моделируемой переменной;
2) зависит от частоты наступления событий;
3) зависит от интегральной вероятности;
4) устанавливается произвольно;
5) равна единице.
Вопрос 4. Для моделирования случайной величины Х в имитационной модели используется метод Монте-Карло. Случайная величина X может принимать значения 6, 7 и 8. При 200 наблюдениях эти значения реализуются с частотами 28, 72 и 100 соответственно. Определите интервал случайных чисел для значения X = 7.
Варианты ответов:
1) от 1 до 28;
2) от 29 до 72;
3) от 15 до 50;
4) от 51 до 100;
5) от 1 до 72.
Вопрос 5. Параметрами управления в имитационной системе управления запасами являются:
1) темп обслуживания и время выполнения заказа;
2) размер запаса и темп производства;
3) величина спроса и время выполнения заказа;
4) размер запаса и время выполнения заказа;
5) издержки хранения и время выполнения заказа.
Задачи
Задача 1. Компания Шустрова обслуживает и сдает внаем квартиры в большом жилом комплексе. Иван Шустров хотел бы оценить предполагаемые затраты на замену компрессоров для кондиционирования воздуха. Он хотел бы определить число компрессоров, выходящих из строя ежегодно в течение 20 лет. Используя данные по аналогичному жилому комплексу, которым его компания владеет в другом городе, Шустров получил относительные частоты выхода компрессоров из строя:
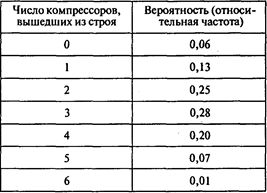
Он решил провести имитационный эксперимент, используя двузначные случайные числа, начиная с числа 37 второй строки таблицы случайных чисел (см. Приложение 2).
Вопросы:
1. Найдутся ли последовательно три года, в каждом из которых из строя выйдет ровно один компрессор?
2. Найдутся ли последовательно три года, в каждом из которых из строя выйдут ровно два компрессора?
Задача 2. Количество машин, прибывающих на автомойку Марка Беззаботного каждый час, за последние 200 часов ее работы приведено в следующей таблице:
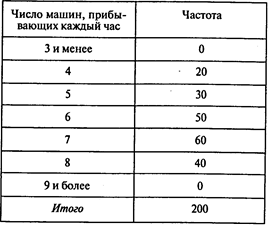
Постройте распределение вероятностей и интегральное распределение вероятностей для количества прибывающих машин. Определите для этой переменной интервалы случайных чисел. Сымитируйте прибытие машин в течение 15 часов работы мойки.
Выберите необходимые для имитации случайные числа из четвертой строки таблицы случайных чисел, начиная со значения 69 (см. Приложение 2).
Вопросы:
1. Сколько машин прибудет в первый час?
2. Сколько машин в среднем прибывает в час?
Задача 3. Груженые баржи, отправляемые вниз по Волге из индустриальных центров, к вечеру достигают Астрахани. Число барж, ежедневно входящих в док, колеблется от 0 до 5. Вероятность прихода 0, 1, ..., 5 барж, а также количество разгружаемых барж и соответствующие вероятности указаны в следующих таблицах:
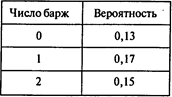
Окончание таблицы
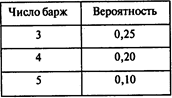
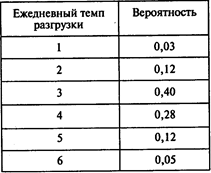
Сымитируйте 15 дней работы порта. Используйте для генерирования числа прибывающих барж случайные числа с начала первой строки таблицы случайных чисел, а для генерирования числа разгруженных барж — с начала второй строки этой таблицы (см. Приложение 2).
Вопросы:
1. Сколько в среднем барж простаивает в день?
2. Сколько в среднем барж приходит ежедневно?
3. Сколько в среднем барж разгружается ежедневно?
Задача 4. Центральный травматологический пункт в Москве имеет шесть отделений:
1) приемное (где может быть оказана неотложная помощь и ставится диагноз) — А;
2) рентгеновское — В;
3) операционное — С;
4) протезное — D;
5) диагностическое (где проводится обследование для уточнения диагноза) — Е;
6) выписки (где оформляются больничные документы и осуществляется оплата) — F.
Вероятности перехода пациента из одного отделения в другое указаны в следующей таблице:
Сымитируйте передвижение в травматологическом пункте для 10 пациентов. Рассматривайте одного пациента в течение всего времени с момента, когда он поступает в приемное отделение, и до момента, когда он выписывается. Вам следует учитывать, что пациент может попадать в одно и то же отделение более одного раза. Используйте для генерирования переходов случайные числа из пятой строки таблицы случайных чисел (см. Приложение 2).
Вопросы:
1. Сколько раз (максимум) один пациент посетит отделение В?
2. Сколько раз в среднем один пациент посетит отделение D?
Задача 5. Штаб военно-воздушной дивизии использует большое количество компьютерных графопостроителей. Графопостроитель наносит на лист бумаги линии в различных направлениях до тех пор, пока не будет сделан весь рисунок. В графопостроителе используется четыре пера различных цветов. Каждое перо может выйти из строя. В этом случае выходит из строя весь графопостроитель и требуется замена соответствующего пера. В штабе замена проводится каждый раз, когда перо выходит из строя. Инженер, обслуживающий графопостроители, предложил при выходе из строя одного пера проводить замену сразу всех четырех перьев. Это должно уменьшить число выходов из строя графопостроителей. На замену одного пера требуется один час, на замену всех четырех перьев — два часа. Стоимость простоя графопостроителя в течение часа 50 тыс. руб. Каждое перо стоит 8 тыс. руб.
Время, проходящее между выходами графопостроителя из строя, распределяется следующим образом:
а) при замене одного пера б) при замене четырех перьев
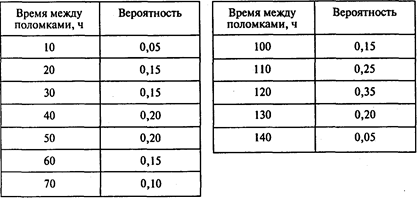
Сымитируйте две различные стратегии и определите лучшую. Используйте для генерирования поломок случайные числа из четвертой строки таблицы случайных чисел (см. Приложение 2). Проведите десять испытаний.
Вопросы:
1. Следует ли заменять сразу все четыре пера?
2. Какую экономию обеспечивает лучшая стратегия в течение месяца работы графопостроителя?
Задача 6. Доктор Елена Прекрасная имеет зубоврачебную практику в Москве. Елена составляет расписание своего приема для того, чтобы пациентам не пришлось долго ожидать. В таблице приведено расписание на 20 мая:
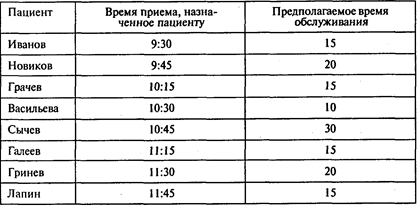
К сожалению, не все пациенты приходят точно к назначенному времени. К тому же и время обслуживания нельзя указать точно. Опыт Елены указывает на то, что:
а) 20% пациентов придут на 20 мин раньше;
б) 10% — на 10 мин раньше;
в) 40% — вовремя;
г) 25% — на 10 мин позже;
д) 5% — на 20 мин позже.
Кроме того:
а) в 15% случаев на обслуживание понадобится на 20% меньше времени, чем указано;
б) в 50% — столько, сколько указано;
в) в 25% — на 20% больше времени;
г) в 10% — на 40% больше времени.
Доктор Елена Прекрасная хотела бы закончить прием 20 мая в 12:15 для того, чтобы вылететь в Минск на конференцию стоматологов. В этот день Елена готова начать прием в 9:30. Пациенты обслуживаются в порядке, указанном в расписании (даже если один пациент приходит раньше, чем назначенный на прием перед ним).
Используйте для генерирования времени прихода и обслуживания пациентов случайные числа из первой строки таблицы случайных чисел (см. Приложение 2).
Вопросы:
1. На сколько минут позже желательного срока закончится прием?
2. Скольким пациентам, пришедшим вовремя, придется ожидать приема?
Задача 7. Магазин Петушкова поддерживает на складе запас 30-ведерных водонагревателей для владельцев индивидуальных домов. Хозяин магазина хотел бы иметь под рукой максимальный запас водонагревателей, чтобы удовлетворить любой спрос. Однако он понимает, что это невыгодно из-за высокой стоимости их хранения. Он проследил за объемом продаж водонагревателей за последние 50 недель и отметил следующее:
Окончание таблицы
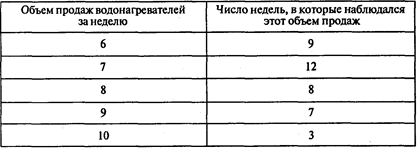
Используйте для имитации седьмую строку таблицы случайных чисел (см. Приложение 2).
Вопросы:
1. Если Петушков будет иметь еженедельный запас в 8 водонагревателей, то сколько раз за 20 недель ему не хватит этого запаса для удовлетворения спроса?
2. Каков объем продаж за 20 недель?
Задача 8. Владелец магазина Петушков уточнил данные о продаже водонафевателей (см. задачу 7), проведя учет за 100 недель, и построил следующее распределение объема продаж:
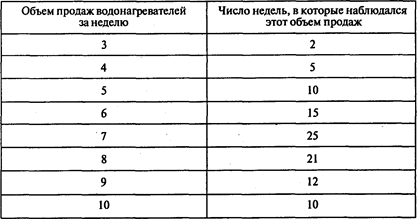
Определите объем упущенных продаж в новых условиях. Используйте для имитации шестую строку таблицы случайных чисел (см. Приложение 2).
Вопросы:
1. Чему равен объем упущенных реализации за 20 недель, если еженедельный запас водонагревателей равен 8?
2. Чему равно среднее число продаж в неделю?
Задача 9. Маша Кондратьева, аспирантка МГУ, испытывает некоторые проблемы с личным бюджетом. Ее доход складывается из стипендии и гонораров за реферативные статьи. Распределение уровня ее доходов в месяц показано в следующей таблице:
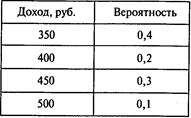
Предполагается, что доход поступает на ее счет и учитывается в начале следующего месяца. Расходы Маши также меняются от месяца к месяцу и подчиняются следующему распределению вероятностей:
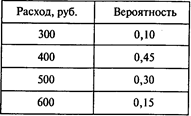
В начале текущего года обучения на ее счете было 600 руб. Сымитируйте текущий год (12 месяцев) и оцените финансовое положение Маши. Предполагается, что реальные расходы Маши не могут превышать суммы на счете. Используйте для имитации шестую строку таблицы случайных чисел (см. Приложение 2).
Вопросы:
1. Сколько месяцев из 12 Маша будет испытывать дефицит бюджета?
2. Какая сумма останется на счете у Маши в конце текущего года?
Задача 10. Даша Василькова — менеджер московского салона фирмы «Мерседес-Бенц». В последние 100 месяцев объем продаж фирмы колеблется от 6 до 12 новых автомобилей. Частота различных объемов продаж показана в следующей таблице:
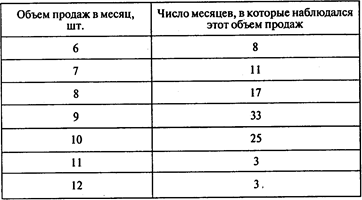
Даша считает, что продажа будет идти в тех же объемах еще 24 месяца. Время выполнения заказа на поставки распределяется следующим образом:
Даша Василькова каждый раз заказывает 21 автомобиль (3 трейлера по 7 автомобилей в каждом); при этом новый заказ можно делать тогда, когда запас в магазине снижается до 12 автомобилей и только после выполнения предыдущего заказа. Сымитируйте эту стратегию в течение 24 месяцев. Используйте для имитации вторую строку таблицы случайных чисел (см. Приложение 2). Считайте, что:
а) начальный запас составляет 28 автомобилей;
б) затраты на хранение одной автомашины составляют в месяц 0,6 тыс. руб.;
в) одна упущенная продажа приносит убыток в среднем 4,35 тыс. руб;
г) один заказ обходится в 0,57 тыс. руб.
Вопросы:
1. Сколько заказов придется сделать за два года?
2. Чему равны издержки данной стратегии?
Задача 11. Фирма «Веста» — производитель промышленных моечных машин. Одной из комплектующих деталей в производственном процессе является стальной лист размером 8 х 10 дм. Сталь поставляется на контрактной основе компанией «Уралсталь», причем еженедельный объем поставок может составлять 8 или 11 тыс. дм2 (45% шансов на то, что объем поставок составит 8 тыс. дм2, и 55% шансов на то, что 11).
Распределение величины потребности в стали показано в следующей таблице:
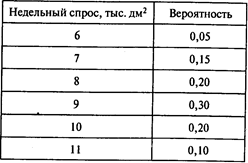
Фирма «Веста» может хранить на складе не более 25 тыс. дм2 стали одновременно.
Сымитируйте заказы на сталь и ее использование в течение 20 недель. Начните первую неделю с нулевого запаса на складе. Если запас на конец недели окажется отрицательным, то восполните необходимую разницу из следующего заказа. Используйте для имитации третью строку таблицы случайных чисел (см. Приложение 2).
Вопросы:
1. Требуются ли фирме «Веста» дополнительные складские помещения?
2. Какое количество стали будет на складе фирмы в конце 20-й недели?
Ситуации
Ситуация 1. Вывоз радиоактивных отходов.
Компания «Байлс» со штаб-квартирой в Дюссельдорфе распоряжается семью специально оборудованными трейлерами для коммерческой транспортировки на большие расстояния радиоактивных отходов. Каждый грузовик совершает в среднем одну поездку в неделю, собирая радиоактивные отходы у химических компаний и других производителей в Центральной Европе. Эти грузы аккуратно доставляются в правительственное хранилище, расположенное недалеко от Дрездена. В настоящее время сбор отходов происходит в восьми странах: Италии, Германии, Австрии, Франции, Бельгии, Нидерландах, Дании и Польше.
Компания «Байлс» имеет офис в столице каждой страны, которую она обслуживает. Персонал офиса включает не только менеджера и секретаря, но и адвоката, по совместительству оказывающего содействие в разрешении политических, общекультурных, пограничных и юридических конфликтов, возникающих в индустрии удаления ядерных отходов.
Сибби Байлс, хозяйка компании, намерена исключить Италию из сферы своего бизнеса. В прошлом году туда было сделано только 25 рейсов за отходами. Хотя текстильное производство в Северной Италии является хорошим полем деятельности для фирмы Байлс, решение о целесообразности сохранить офис и вести деловые операции в этой стране следует принимать с учетом объема работы и получаемого дохода.
Чтобы проанализировать рынок Италии, Байлс собрала данные об объеме перевозок и доходов за прошедший год. Каждый из 25 трейлеров, загруженных в Италии в прошлом году, собрал от 26 до 50 баррелей отходов:
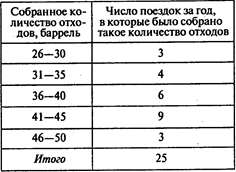
Доход, получаемый за баррель отходов (изменяется от 50 до 80 евро), зависит от типа радиоактивных материалов и количества вывозимых отходов:
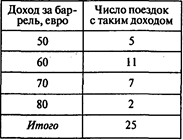
Байлс решила, что имитация 25 грузовых поездок из Италии позволит оценить рентабельность работы в этой стране в следующем году.
Она определила, что каждая поездка к дрезденскому хранилищу обходится в 900 евро, включая зарплату водителя, оплату топлива и амортизацию грузовика. Прочие накладные расходы составляют 120 евро на поездку. Содержание офиса в Италии обходится в 41 тыс. евро в год. Эта сумма включает зарплату и косвенные накладные расходы, которые несет штаб-квартира в Дюссельдорфе.
Задания
1. Определите, позволят ли доходы от поездок в Италию покрыть расходы на содержание офиса в этой стране.
2. Предложите стратегию проведения имитационного эксперимента.
3. Проведите имитационный эксперимент для оценки годовых доходов компании «Байлс» в Италии.
4. Проведите аналитические расчеты для оценки ожидаемого годового дохода и сравните результаты с результатами имитационного эксперимента.
(Переработано из: Heizer J., Render В. Production and Operations Management. — Boston: Allyn and Bacon, 1993)
Ситуация 2. Вывоз грузов из порта.
После завершения высшего образования в США Самир Кальдон вернулся в Саудовскую Аравию, где его семья вела собственное дело. Ближайшей целью Самира было реконструировать и стабилизировать принадлежащую его семье транспортную компанию «Перевозки Кальдона».
Самир столкнулся с проблемой определения числа грузовиков, необходимых для перевозки предполагаемого количества грузов. До сих пор грузовики приобретались по мере необходимости без всестороннего планирования объема перевозок. Следствием такого подхода были проблемы с наймом водителей и обслуживанием грузовиков, а также выплата неустоек за несвоевременный вывоз грузов из порта и возврат контейнеров.
Штрафы за простой грузов в порту очень велики. Они рассчитываются по следующему правилу.
1. Для вывоза груза из порта отводится 10 дней (не облагаемый штрафом период);
2. После этого за каждые 24 часа простоя в порту 1 т груза взимается штраф размером в один реал (приблизительно равен одному американскому доллару). За следующие 24 часа взимается штраф два реала, за следующие 24 часа — три реала и т.д.
По прогнозу Самира, объем перевозимого компанией груза составляет в среднем 160 тыс. т в месяц со стандартным отклонением 30 тыс. т. Темп поступления груза в течение месяца является постоянным. В соответствии с предыдущим опытом количество грузов, перевозимых компанией в течение месяца, имеет нормальное распределение.
После длительных исследований Самир пришел к заключению, что автопарк должен быть укомплектован 40-футовыми грузовиками Мерседес 2624 с грузовыми платформами, каждый из которых может перевозить или два 20-футовых контейнера, или один 30-футовый, или один 40-футовый контейнер. Максимальная грузоподъемность одного грузовика 60 т. Стоимость одного грузовика 240 тыс. реалов. К тому же грузовик должен быть адаптирован для использования в Саудовской Аравии: иметь двойную систему охлаждения, радиатор повышенного объема и специальные высокотемпературные шины. Практика показывает, что вероятность безотказной работы такого грузовика равна 0,96.
Приблизительно 25% поступающих грузов упакованы в контейнеры длиной 20, 30 или 40 футов. Остальные 75% груза не упакованы в контейнеры. Двадцатифутовый контейнер вмещает приблизительно 20 т груза, 30-футовый — 45 т, 40-футовый — 60 т. Приблизительно 60% контейнеризированных грузов находятся в 40-футовых контейнерах, 20% — в 30-футовых и 20% — в 20-футовых контейнерах.
Использование контейнеров связано со следующими штрафными санкциями.
1. Пять дней (не облагаемый штрафом период) отводится для того, чтобы вернуть контейнер в порт.
2. За каждые 24 часа задержки контейнера сверх этого срока взимается штраф 1000 реалов, за следующие 24 часа — 2000 реалов, следующие — 3000 реалов и т.д.
Компания «Перевозки Кальдона» забирает груз в порту и доставляет его либо непосредственно потребителю, либо на склад для последующей транспортировки.
Основываясь на этих данных, Самир пришел к выводу, что каждый грузовик должен брать груз в порту 3 раза в день.
Финансовый анализ показывает, что прибыль от доставки 1 т груза составляет в среднем 2,25 реала. Альтернативные издержки капитала, инвестированного компанией Кальдона, составляют 20%.
Задания
1. Разработайте имитационную модель, учитывающую все факторы, влияющие на принятие решения.
2. Проведите расчеты и определите, сколько грузовиков следует иметь компании.
(Переработано из: Render В., Stair R.M., Greenberg I. Cases and Readings in Management Science. – Boston, Allyn and Bacon, 1988)
Ответы и решения
Ответы на вопросы:1—3, 2 — 3, 3 — 2, 4 — 3, 5 — 4.
Задача 1. Решение.
Построим таблицу интегрального распределения вероятности и установим интервалы случайных чисел:
Дата добавления: 2016-07-09; просмотров: 2422;