Классификационные признаки систем массового обслуживания. 4 страница
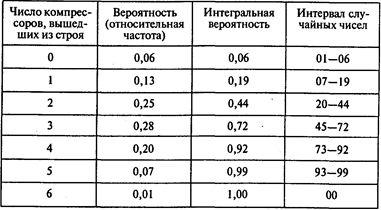
Сымитируем выходы компрессоров из строя в течение 20 лет:
Количество выходов из строя за 20 лет равно 53. За год в среднем выйдет из строя 53/20 = 2,65 компрессора.
Ответы: 1. Нет, не найдутся. 2. Нет, не найдутся.
Задача 2.Решение.
Построим распределение вероятностей и интегральное распределение вероятностей для количества прибывающих машин, определим интервалы случайных чисел:
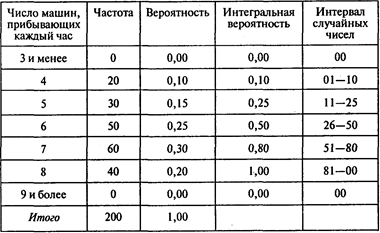
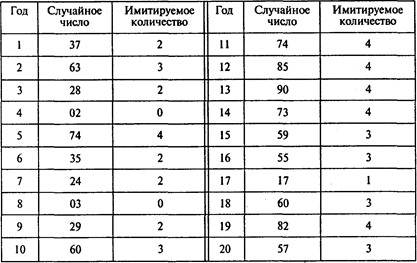
Сымитируем прибытие машин:
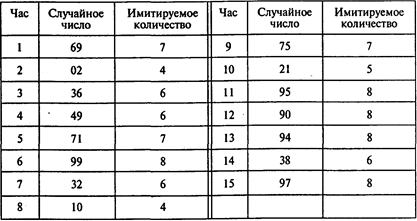
Общее количество прибывших машин в течение 15 часов равно 98.
Ответы: 1. Семь машин. 2. 6,5 машины.
Задача 3. Решение.
Определим интегральную вероятность и интервалы случайных чисел для количества прибывающих барж:
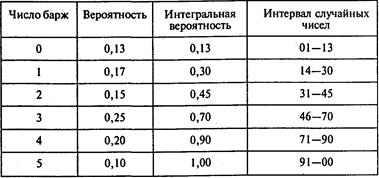
Определим интегральную вероятность и интервалы случайных чисел для количества разгруженных барж:
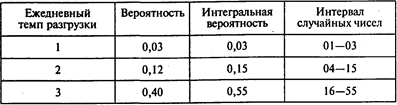
Окончание таблицы
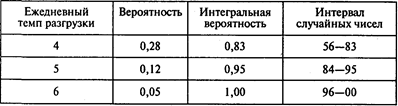
Сымитируем 15 дней работы порта (СЧ— случайное число):
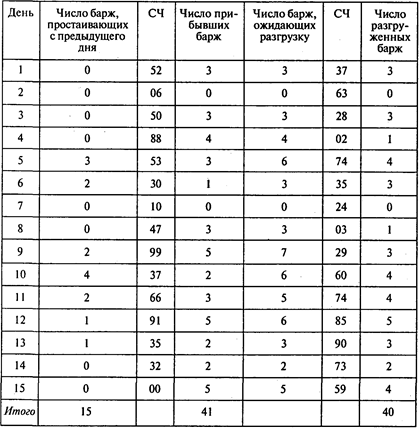
В среднем простаивает 15/15 = 1 баржа вдень.
Ежедневно приходит в среднем 41/15 = 2,73 баржи, а разгружается 40/15 = 2,67 баржи.
Ответы: 1. Одна баржа. 2. 2,73 баржи. 3. 2,67 баржи.
Задача 4. Решение.
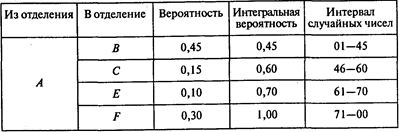
Построим интервалы случайных чисел для каждого отделения:
1) приемное
2) рентгеновское
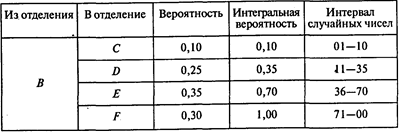
3) операционное
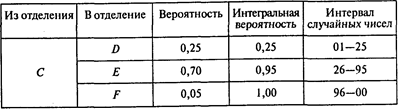
4) протезное
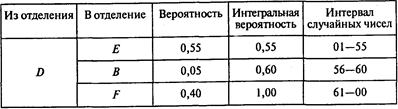
5) диагностическое
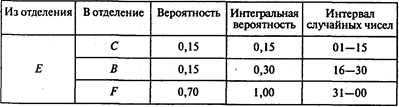
Имитация (О — отделение; СЧ — случайное число):
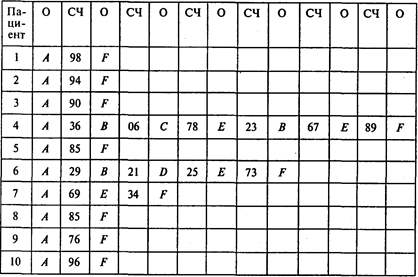
Ответы: 1. Два раза. 2. 0,1 раза.
Задача 5. Решение.
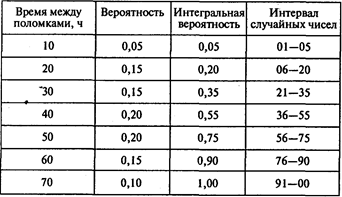
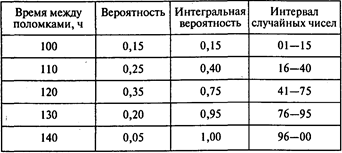
Построим интервалы случайных чисел для времени между поломками:
а) при замене одного пера
б) при замене четырех перьев
Имитация с одним пером:
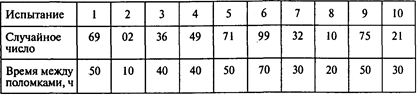
В среднем одно перо отработает 39 часов. В течение месяца одно перо выйдет из строя 720/39 = 18,5 раза.
Затраты, связанные с заменой одного пера, составят
18,5 • (50 + 8) = 1073 тыс. руб.
Имитация с четырьмя перьями:
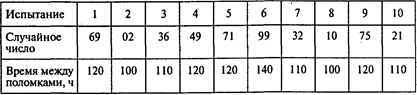
В среднем четыре пера отработают 115 часов. В течение месяца четыре пера выйдут из строя 720/115 = 6,3 раза.
Затраты по замене четырех перьев составят
6,3 • (2 • 50 + 4 • 8) = 831,6 тыс. руб. Экономия при использовании лучшей стратегии составит
1073 – 831,6 = 241,4 тыс. руб.
Ответы: 1. Да, следует. 2. 241,4 тыс. руб.
Задача 6. Решение.
Построим интервалы случайных чисел для прихода и времени обслуживания пациентов:
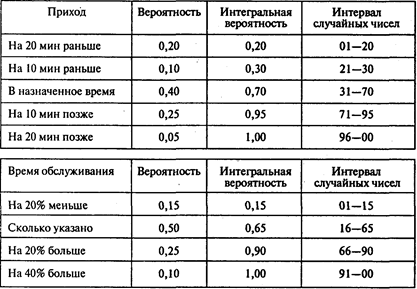
Сымитируем приход и обслуживание пациентов (СЧ — случайное число):
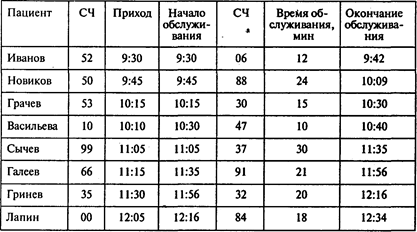
Ответы: 1. На 19 мин. 2. Двум пациентам.
Задача 7. Решение.
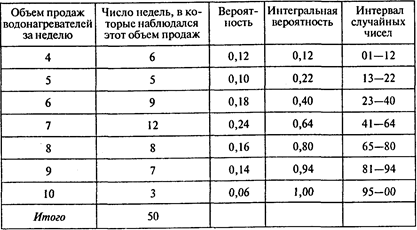
Имитация продаж:
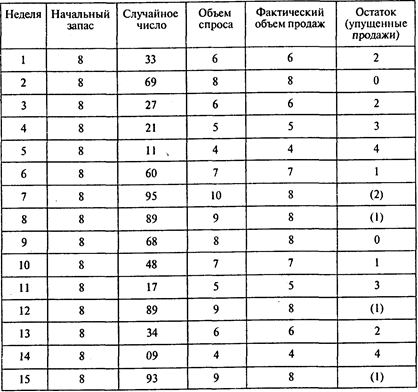
Окончание таблицы
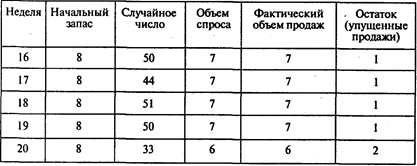
Ответы: 1. Четыре раза. 2. 132 водонагревателя.
Задача 8. Решение.
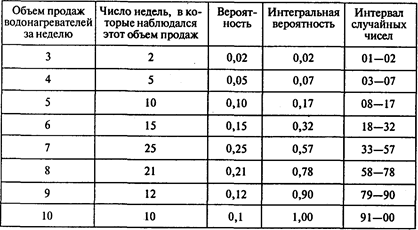
Имитация продаж:
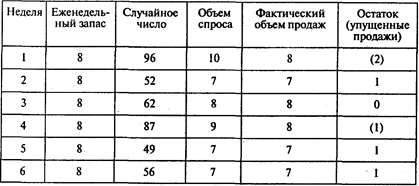
Окончание таблицы
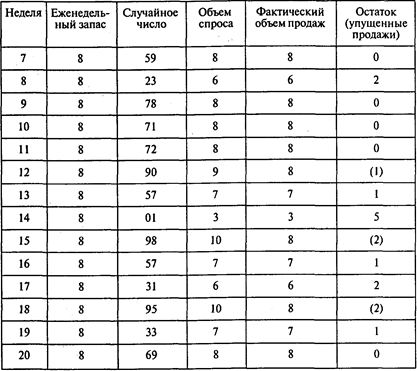
Ответы: 1. Восемь водонагревателей. 2. 7,25.
Задача 9. Решение.
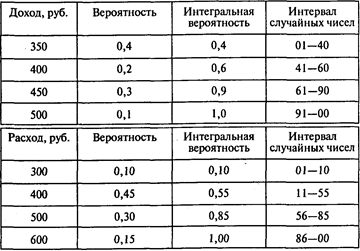
Имитация (СЧ — случайное число):
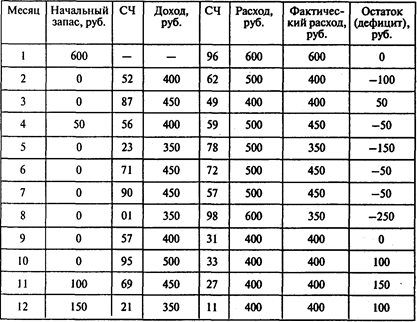
Ответы: 1. Шесть месяцев, 2.100руб.
Задача 10. Решение.
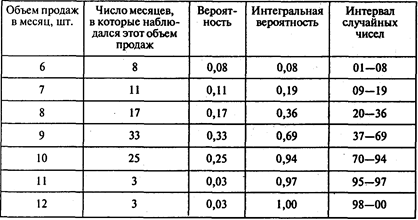
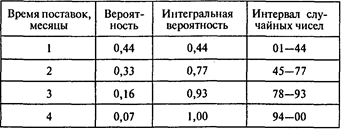
Имитация (СЧ — случайное число):
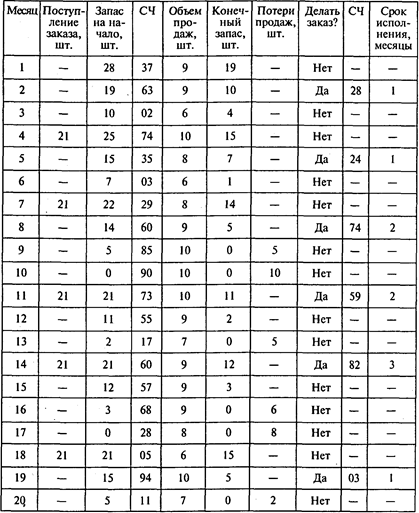
Окончание таблицы
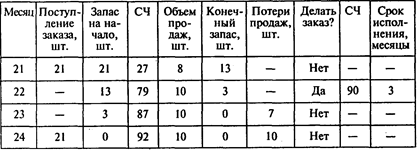
Сумма затрат за два года составит 7 • 0,57 + 139 • 0,6 + 53 • 4,35 = 317,94 тыс. руб.
Ответы: 1. Семь заказов. 2. 317,94 тыс. руб.
Задача 11. Решение.
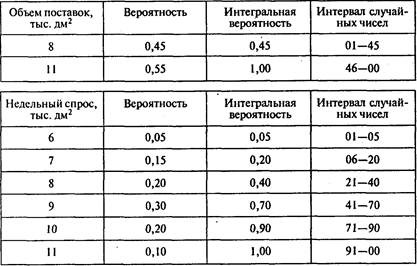
Имитация заказов (СЧ — случайное число):
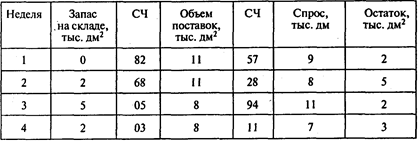
Окончание таблицы
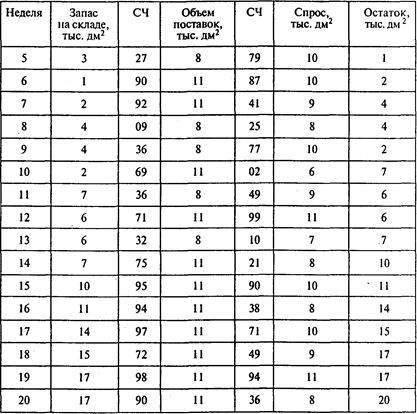
Ответы: 1. В течение 20 недель не требуются. 2. 20 тыс.дм2.
Глава 15. Целочисленные задачи линейного программирования
Цели
Нередко приходится рассматривать задачи, в которых неизвестные величины могут принимать только целочисленные значения. Например, задачи, связанные с определением необходимого числа рабочих мест или количества дорогостоящих станков. При решении таких задач с целочисленными переменными методы линейного (выпуклого) программирования неприменимы.
Другая сфера применения целочисленных моделей — выбор вариантов. В соответствующих задачах все или некоторые переменные могут принимать только два значения: 0 или 1. Такие переменные носят название булевых.
Наиболее известные методы решения целочисленных задач — метод отсечения и метод ветвей и границ. Они разработаны в начале 60-х годов XX века и затем неоднократно усовершенствовались и модифицировались. Решения примеров и задач, приводимых в этой главе, получены с помощью метода ветвей и границ и являются точными.
После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь использовать для экономического анализа следующие понятия:
• неделимость;
• целочисленная задача;
• целочисленная и булева переменные;
• взаимоисключение и взаимообусловленность.
Модели
Дискретные (целочисленные) задачи математического программирования могут возникать различными путями. Существуют задачи линейного программирования, которые формально к целочисленным не относятся (требование целочисленности переменных в них в явном виде не накладывается), но которые при целочисленных исходных данных всегда обладают целочисленным планом. Этим свойством обладают транспортная задача и различные ее варианты (задача о назначениях).
Первоначальным стимулом к изучению целочисленных и дискретных задач явилось рассмотрение задач линейного программирования, в которых переменные представляли физически неделимые величины (скажем, количество единиц продукции разных видов). Для характеристики этого класса моделей используется термин «задачи с неделимостями».
Другим важным толчком к построению теории дискретного программирования явился новый подход к некоторым экстремальным комбинаторным задачам, для решения которых приходится вводить булевы переменные, носящие логический характер (х = 1 или х = 0).
К целочисленным (точнее, частично целочисленным) задачам линейного программирования удается свести также ряд задач, в которых явное требование целочисленности отсутствует, зато имеются некоторые особенности, выводящие их за рамки линейного программирования. Эти особенности могут относиться либо к целевой функции, либо к области допустимых решений.
Итак, можно выделить следующие основные классы задач дискретного программирования:
1) транспортная задача (см. главу 5) и ее варианты;
2) задачи с неделимостями;
3) экстремальные комбинаторные задачи;
4) задачи с неоднородной разрывной целевой функцией (см. транспортную задачу с фиксированными доплатами в главе 5);
5) задачи на неклассических областях (см. модель оптимального размера заказа с количественными скидками в главе 12).
Целочисленная задача линейного программирования (задача с неделимостями). К данному классу принадлежат задачи распределения капиталовложении и задачи планирования производства.
Целочисленная задача линейного программирования заключается в максимизации функции:
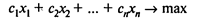 (1)
(1)
при условиях
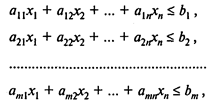 (2)
(2)
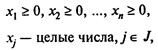
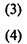
где J — некоторое подмножество множества индексов N = ={1,2,...,n}.
Если J = N (T.e. требование целочисленности наложено на все переменные), то задачу называют полностью целочисленной; если же J ¹ N, она называется частично целочисленной.
Модель (1)—(4) естественно интерпретировать, например, в следующих терминах. Пусть через i = 1,..., т обозначены производственные факторы, через j = 1, ..., п — виды конечной продукции.
Обозначим далее:
aij — количество факторов i, необходимое для производства единицы продукта j;
bi — наличные ресурсы фактора i;
сi — прибыль, получаемая от единицы продукта j.
Пусть продукты j для jÎJ являются неделимыми, т.е. физический смысл имеет лишь их целое неотрицательное количество («штуки»). Предположим, что требуется составить производственную программу, обеспечивающую максимум суммарной прибыли и не выводящую за пределы данных ресурсов. Обозначая через xj искомые объемы выпуска продукции, мы сводим эту задачу к модели (1)-(4).
Задача с булевыми переменными. Логическая взаимосвязь:
1) взаимоисключение. Пусть xj = 1, если реализуется проект Аj, и хj = 0 в противном случае. Запись AjÚAk означает, что в план может быть включен либо проект Аj, либо проект Аk. Вместе они включены быть не могут. С помощью этой записи выражается отношение взаимоисключения между проектами.
В этих обозначениях взаимоисключение Aj Ú Аk выражается неравенством хj + хk £ 1;
2) взаимообусловленность. Запись Аk ® Aj («проект Аk влечет за собой проект Аj») означает, что проект Аk может быть включен в план только в том случае, если в план включен и проект Aj. С помощью этой записи выражается отношение между обусловливающими друг друга проектами, например когда проект Ak — результат тиражирования проекта Aj на другом объекте или когда Аk базируется на результатах реализации проекта Aj.
В принятых обозначениях взаимообусловленность Аk ® Аj выражается неравенством хk £ хj.
Экстремальные комбинаторные задачи. Задачи данного класса, называемые также задачами выбора, состоят в отыскании среди конечного множества альтернатив одной, которой отвечает экстремальное значение принятой целевой функции.
Задача о коммивояжере — классический пример задачи выбора оптимального маршрута. Формулируется она следующим образом. Коммивояжер должен выехать из определенного города и вернуться в него, побывав в каждом из городов лишь по одному разу и проехав минимальное расстояние.
Пусть хij = 1, если коммивояжер переезжает из города i непосредственно в город j, и xij = 0 в противном случае. Обозначим через сij расстояние между городами i и j (чтобы избежать бессмысленных значений хij = 1, предполагается, что сii равны достаточно большому числу).
Тогда формальная модель имеет вид
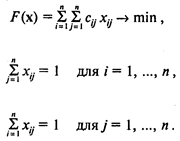
К приведенным ограничениям необходимо добавить условия на недопустимость подциклов, т.е. повторного посещения городов (за исключением исходного). Это ограничения вида
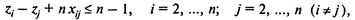
где на переменные zi и zj не требуется накладывать никаких ограничений.
Общая задача календарного планирования формулируется следующим образом. Имеется п станков (машин), на которых требуется обработать m деталей. Заданы маршруты (в общем случае различные) обработки каждой детали на каждом из станков или группе станков. Задана также продолжительность операций обработки деталей. Предполагается, что одновременно на станке можно обрабатывать не более одной детали. Требуется определить оптимальную последовательность обработки. Критерием оптимальности могут выступать продолжительность обработки всех деталей, суммарные затраты на обработку, общее время простоя станков и др. Существует огромное число постановок данной задачи, учитывающих конкретные условия производства.
Один из представителей задач данного типа — так называемая задача о ранце. Имеется п предметов. Предмет j (j = 1, ..., п) обладает весом wj и полезностью сj. Пусть b — общий максимально допустимый вес предметов, которые можно положить в ранец. Требуется выбрать предметы таким образом, чтобы их общий вес не превышал максимально допустимый и при этом суммарная полезность (ценность) содержимого ранца была максимальной. Пусть хj = 1, если предмет положен в ранец, и хj = 0 в противном случае. Математическая формулировка задачи имеет вид
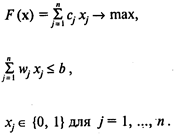
К классу экстремальных комбинаторных задач принадлежит также линейный и нелинейный варианты задача о назначениях (линейный вариант такой задачи рассмотрен в главе 6).
Большинство целочисленных и комбинаторных типов задач, таких, как задача с неделимостями, задача коммивояжера, задача календарного планирования, принадлежит к разряду так называемых трудно решаемых. Это означает, что вычислительная сложность алгоритма их точного решения — зависимость числа элементарных операций (операций сложения или сравнения), необходимых для получения точного решения, от размерности задачи я — является экспоненциальной (порядка 2n), т.е. сравнимой по трудоемкости с полным перебором вариантов. В качестве п, например, для задачи с неделимостями служит число целочисленных переменных и число ограничений, для задачи коммивояжера — число городов (или узлов графа маршрутов), для задачи календарного планирования — число деталей и число станков. Такие задачи называют еще NP-трудными или NP-полными. Получение их точного решения не может быть гарантировано, хотя для некоторых задач данного типа существуют эффективные методы, позволяющие находить точное решение даже при больших размерностях. Примером таких задач служит задача о ранце с булевыми переменными.
Задачи с вычислительной сложностью, определяемой полиномиальной зависимостью от п, называются эффективно решаемыми. К такого типа задачам принадлежат задачи транспортного типа и линейные задачи о назначениях.
Для решения целочисленных задач используются следующие методы:
1) симплекс-метод (для транспортных задач, задач о назначениях);
2) метод отсечения (метод Гомори);
3) метод ветвей и границ (в общем случае не обеспечивает получения точного решения);
4) эвристические методы (не обеспечивают получения точного решения).
Последняя группа методов может использоваться в случаях, когда применение предыдущих методов невозможно или не приводит к успеху. Кроме того, эвристические методы можно использовать для решения задач любой сложности.
Примеры
Пример 1. Оптимизация капиталовложений.
Имеется 10 работ (А1 ¸ А2), каждая из которых характеризуется тремя технико-экономическими показателями:
аj — трудозатраты;
bj — размер, необходимых капиталовложений;
сj — ожидаемый экономический эффект.
Исходные данные приведены в следующей таблице:

Общие трудозатраты не должны превышать 20. Общий объем капиталовложений не должен превышать 20. Определите, какие из 10 работ следует выполнить, чтобы максимизировать ожидаемый экономический эффект, учитывая следующие условия взаимообусловленности и взаимоисключения:
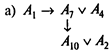
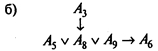
Решение. Помимо целевой функции и двух ограничений по общему объему трудозатрат и капиталовложений, данную задачу характеризует следующая система неравенств:
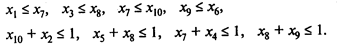
В результате расчетов получаемх* = (0101110010).
Пример 2. Оптимизация производственной программы.
Автомобилестроительный завод выпускает три модели автомобилей, которые изготавливаются последовательно в трех цехах. Мощность цехов составляет 300, 250 и 200 человекодней в декаду. В первом цехе для сборки одного автомобиля первой модели требуется б человекодней, второй модели — 4 и третьей модели — 2 человекодня в декаду соответственно. Во втором цехе трудоемкость равна 3,4 и 5 человекодней соответственно, в третьем — по 3 человекодня на каждую модель. Прибыль, получаемая заводом от продажи одного автомобиля каждой модели, составляет соответственно 15, 13 и 10 тыс. долл.
Постройте модель для определения оптимального плана.
Решение. Пусть хi — количество выпускаемых автомобилей i-й модели в течение декады (i = 1,..., n). В принятых обозначениях модель имеет вид
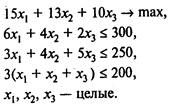
Пример 3. Двумерная задача раскроя.
Из минимального количества листов стекла размером 8 х 6 м2 требуется вырезать 10 оконных стекол размером 4 х 4 м2, 20 оконных стекол размером 4 х 5 м2 и 30 оконных стекол размером 3х3 м2. Множество вариантов раскроя (см. главу 3) показано в следующей таблице:
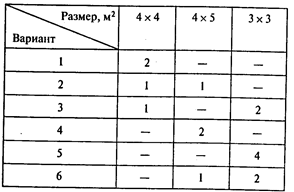
Построите модель для определения плана раскроя, требующего минимального количества материала.
Решение. Пусть хi — количество листов стекла размером 8 х 6 м2, которые следует раскроить по варианту i.
Тогда модель имеет вид
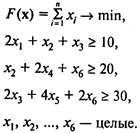
Пример 4. Задача о ранце.
Некая торговая компания имеет свои универсамы в Москве, Санкт-Петербурге, Нижнем Новгороде, Екатеринбурге, Самаре, Воронеже и Казани. В результате ошибок менеджмента экономическое положение компании стало ухудшаться, ей пришлось взять кредит в размере 13 млн руб. и в конечном счете, чтобы вовремя его погасить, срочно продавать некоторые из своих универсамов. Средства, которые компания могла бы получить от продажи универсамов в Москве, Санкт-Петербурге, Нижнем Новгороде, Екатеринбурге, Самаре, Воронеже или Казани, составляют соответственно 5,2; 4,9; 4,5; 3,6; 3,4; 3,2 и 3,1 млн руб. Однако продажа универсамов сопряжена с необходимостью увольнения персонала. Его численность составляет соответственно 200,190,180,170, 150,130 и 110 человек. По требованию объединенного профсоюза работников торговли компания должна минимизировать численность увольняемого персонала.
Постройте модель для нахождения оптимального решения.
Решение. Пронумеруем города в соответствии с порядком их перечисления. Пусть хi = 1, если универсам, расположенный в городе, продается, и хi = 0 в противном случае. Тогда оптимизационная модель имеет вид
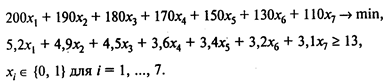
Вопросы
Вопрос 1. В задаче оптимального выбора проектов развития предприятия сформулировано дополнительное условие: реализация первого проекта возможна только в случае реализации хотя бы одного из двух проектов — второго или третьего.
Пусть хi = 1, если вариант i реализуется, и хi = 0 в противном случае. Тогда дополнительное условие может быть формализовано в виде:
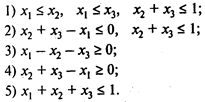
Вопрос 2. В задаче оптимального выбора проектов развития предприятия сформулировано дополнительное условие: реализация первого проекта возможна в случае реализации хотя бы одного из двух проектов — второго или третьего, причем хотя бы один из них должен быть реализован.
Пусть хi = 1, если вариант i реализуется, и xi = 0 в противном случае. Тогда дополнительное условие может быть формализовано в виде:
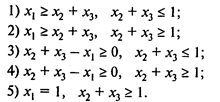
Вопрос 3. Задача какого типа из указанных ниже не обязательно содержит хотя бы одну целочисленную переменную:
1) унимодулярная задача с целочисленной исходной информацией;
2) задача с неоднородной разрывной целевой функцией;
3) комбинаторная задача;
4) задача с неделимостями;
5) производственно-транспортная задача.
Вопрос 4. Задача целочисленного линейного программирования
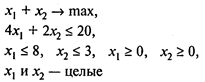
заменой переменных сведена к задаче линейного программирования с булевыми переменными. Чему равно минимальное число переменных в новой задаче?
Варианты ответов:
1) 2; 2) 3; 3) 5; 4) 6; 5) 7.
Задачи
Задача 1. Руководство завода предполагает провести комплекс организационно-технических мероприятий в целях модернизации производства. Мероприятия потребуют следующих затрат производственных площадей, трудовых и финансовых ресурсов:
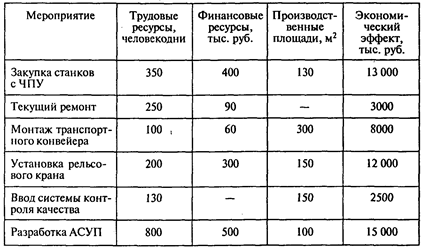
На реализацию всех мероприятий завод может выделить трудовых ресурсов 1300 человекодней, финансовых — 10 млн руб., производственных площадей — 700 м2.
Определите мероприятия, которые следует провести, располагая этими ресурсами, с тем чтобы общий экономический эффект был максимальным.
Вопросы:
1. Каков максимальный экономический эффект от проведения мероприятий?
2. Какое количество мероприятий следует провести?
Задача 2. В текущем году заводу необходимо:
1) закупить два универсальных станка с ЧПУ общей стоимостью 200 тыс. руб. Для этого требуются трудовые ресурсы в объеме 250 человекодней и производственные площади 100 м2;
2) смонтировать транспортный конвейер стоимостью 100 тыс. руб. Необходимы трудовые ресурсы 190 человекодней и производственные площади 200 м2.
Для проведения этих мероприятий завод располагает финансовыми ресурсами 250 тыс. руб., трудовыми — 200 человекодней и производственными площадями 200 м2.
Недостаток средств и ресурсов можно компенсировать, проведя некоторые из следующих мероприятии:
1) внедрить новые резцы для обработки металла. Экономия трудозатрат — 130 человекодней, финансовые затраты — 50 тыс. руб.;
2) провести профилактический ремонт станочного парка. Трудозатраты — 10 человекодней, прибыль — 20 тыс. руб.;
3) внедрить систему контроля качества продукции. Экономия трудозатрат — 190 человекодней, затраты производственных площадей — 50 м2, прибыль — 5 тыс. руб.;
4) реализовать устаревшее оборудование. Трудозатраты — 60 человекодней, высвобождение производственных площадей — 200 м2, прибыль — 300 тыс. руб.;
5) провести инвентаризацию запасов материальных ресурсов. Трудозатраты — 20 человекодней, высвобождение производственных площадей — 150 м2.
Вопрос: Какое минимальное количество мероприятий следует провести, чтобы закупить станки с ЧПУ и смонтировать транспортный конвейер?
Задача 3. В Сибири работают четыре химических завода. Они участвуют в конкурсе на размещение госзаказа по производству изделий пяти наименований в следующем объеме:

Каждый завод представил несколько вариантов годовой производственной программы по выполнению госзаказа и соответствующие финансовые условия контракта:
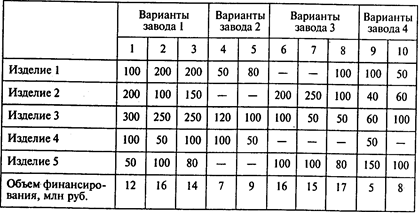
Вопросы:
1. Каковы минимальные затраты на выполнение заказа?
2. Следует лиреализовать вариант 2 завода 1?
Задача 4. Нефтеперерабатывающее предприятие использует в производстве нефть трех сортов. Резервные запасы нефти каждого сорта должны быть не меньше соответственно 20,40 и 60 тыс. т. Для хранения нефти могут быть использованы четыре резервуара вместимостью 25, 30, 35,40 тыс. т. Затраты на хранение 1 т нефти сорта 2 на 10% выше, чем затраты для нефти сорта 1, а для сорта 3 на 20% выше, чем для сорта 1. Смешение нефти разных сортов при хранении не допускается.
Вопросы:
1. Сколько резервуаров следует использовать?
2. Нефть какого сорта следует хранить в резервуаре вместимостью 30 тыс. т?
Задача 5. Объединение кабельной промышленности состоит из трех заводов. Номенклатура выпускаемых изделий включает три позиции: кабель силовой, провод для осветительных установок и провод обмоточный. На трехлетний период планирования разработаны три варианта развития завода 1, два варианта развития завода 2 и один — завода 3. Производство кабельных изделий (в тыс. м) по годам приведено в следующей таблице:
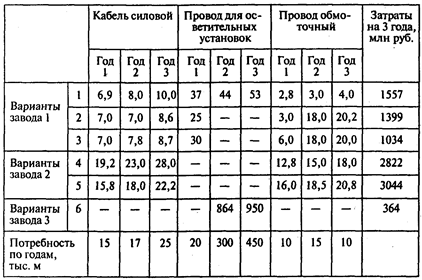
Определите план выпуска продукции на трех заводах, обеспечивающий удовлетворение заданной потребности в кабельных изделиях с минимальными затратами.
Вопросы:
1. Каковы минимальные затраты?
2. Следует ли использовать вариант 3 для завода 1?
Задача 6. В последующие два года добыча угля К2 должна возрасти на 180 и 234 тыс. т соответственно, а угля СС — на 150 и 195 тыс. т. Для обеспечения роста добычи могут быть введены в действие три шахты. Для каждой из них разработаны два варианта добычи угля. Для первого года с момента ввода шахты данные по объемам добычи (тыс. т) приведены в следующей таблице:
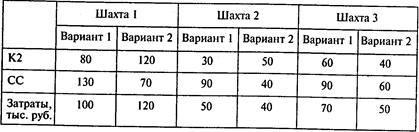
Дата добавления: 2016-07-09; просмотров: 1969;
