Классификационные признаки систем массового обслуживания. 2 страница

Рассматриваются следующие возможные конфигурации системы:

А. Одноканальная система с одним служащим, выполняющим заказы и принимающим оплату. Среднее время обслуживания клиента — 2 мин.

В. Одноканальная система с одним служащим, выполняющим заказ, и другим служащим, принимающим оплату. Среднее вре­мя обслуживания — 1,25 мин.

С. Двухканальная система с двумя служащими, каждый из ко­торых выполняет заказы и принимает оплату. Среднее время об­служивания — 2 мин для каждого из служащих.

Для каждой конфигурации системы определите:

вероятность того, что в системе нет машин;

среднее число машин в очереди;

среднее время ожидания обслуживания;

среднее время пребывания в системе;

среднее число машин в системе;

вероятность того, что вновь прибывшей машине придется ждать.

Вопрос: Какой из вариантов требует меньших затрат?

Задача 7. Механики компании «Автосервис» прибывают на главный склад за запчастями со средней скоростью 4 механика в минуту. Сейчас на складе один работник. Каждый механик в сред­нем находится на складе 4 мин. Найдите:

среднее число клиентов в системе;

среднее время обслуживания одного клиента в системе;

среднее число клиентов в очереди.

Опыт использования двух работников на складе показал, что время ожидания механиком своей очереди снизилось. Определи­те для двухканальной системы:

среднее число клиентов в системе;

среднее время обслуживания одного клиента в системе;

среднее число клиентов в очереди.

Механик получает 1200 руб. в час, а работник отдела запчас­тей — 720 руб. в час.

Вопрос: Какая из двух систем (одноканальная или двухканаль­ная) более экономична?

Задача 8. Автоматическая мойка машин может обслужить 10 машин в час. Машины прибывают по закону Пуассона со сред­ней скоростью 24 автомашины за 8-часовой рабочий день. Систе­ма одноканальная.

Вопросы:

1. Чему равно среднее число автомобилей в очереди?

2. Чему равно среднее время ожидания?

3. Какую часть рабочего времени система занята?

Задача 9. Компания «Жалюзи на дом» решила довести число своих машин до 8. Президент компании интересуется, стоит ли в этом случае нанимать на работу второго механика в помощь к одному имеющемуся. Средняя скорость прибытия на ремонт равна 0,05 раза в час для каждой машины, средняя скорость обслужива­ния — 0,5 машины в час. Каждый механик получает 20 долл. в час, а стоимость простоя машины составляет 80 долл. в час.

Рассчитайте следующие операционные характеристики, если компания оставляет единственного механика:

вероятность того, что все машины работают и механик простаи­вает;

среднее число ожидающих ремонта машин;

среднее число машин в системе (машины в очереди и на об­служивании);

среднее время ожидания начала ремонта;

среднее время нахождения в системе (ожидание и ремонт).

Используя компьютерную программу, рассчитайте те же харак­теристики для случая с двумя механиками.

Вопрос: Сколько механиков следует нанять с экономической точки зрения?

Задача 10. В распоряжении магазина находится 10 грузовиков. Грузовики прибывают в магазин в случайном порядке в течение дня для погрузки-разгрузки. Каждый грузовик прибывает на об­служивание дважды за 8-часовой рабочий день. Средняя скорость обслуживания — 4 грузовика в час. Поток грузовиков описывает­ся пуассоновским распределением, время обслуживания — экспо­ненциальным. Определите:

вероятность того, что ни один грузовик не ожидает погрузки-разгрузки;

среднее число грузовиков в очереди;

среднее число грузовиков у магазина (грузовики в очереди и на погрузке-разгрузке);

среднее время ожидания в очереди.

Вопрос: Каковы часовые издержки по функционированию си­стемы, если в час издержки на кажцый грузовик рав­ны 50 долл., а на работы с грузовиками — 30 долл.?

Ситуации

Ситуация 1. Супермаркет «Север».

«Север» — недавно открытый супермаркет в Северном адми­нистративном округе Москвы, где существует большая конкурен­ция между подобными магазинами. Новый управляющий Петр Перфилов понимает, что при высокой конкуренции покупатели скорее пойдут туда, где им предложат лучшее обслуживание и более широкий ассортимент товаров. Он гордится своим магази­ном, большим выбором различных сортов мяса и сыра, а также мясным прилавком, где покупатель может попробовать нарезки мяса и птицы.

Петр уверен, что быстрое и эффективное обслуживание может привлечь покупателей и повысить конкурентоспособность. Он ввел систему безналичных расчетов за покупки и внедрил службу «Доставка на дом», чтобы сделать приобретение покупок более удобным, особенно для пожилых горожан. Следующий этап — установка новых кассовых аппаратов, недавно появившихся в сфе­ре обслуживания. Основной вопрос: сколько аппаратов следует установить? Слишком много — нежелательно. Но не потому, что появятся дополнительные издержки. Более важный аспект — эф­фективное использование площадей.

Планируя новый дизайн системы контроля, Петр собрал дан­ные о нескольких последовательных субботних, наиболее посеща­емых, утренних часах в своем магазине. Он заметил, что покупа­тели прибывают на контроль приблизительно по 10 человек в час. 20% покупателей оплачивают 10 или менее наименований продук­тов, и в среднем их обслуживают в течение 2 мин, в то время как на покупателей с более чем 10 товарами кассир затрачивает по 4 мин.

Задание

Помогите Петру определить, сколько новых кассовых аппара­тов следует установить.

Ответы и решения

Ответы на вопросы: 1—4, 2 — 3, 3—2, 4—4, 5—2, 6—1.

Задача 1. Решение.

Рассматриваем модель А.

Среднее число клиентов в очереди

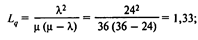
среднее число клиентов в системе

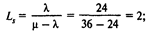
среднее время ожидания

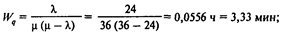
среднее время, которое клиент проводит в системе,

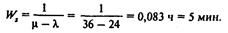
В среднем за 5 мин прибывают (24 : 60) • 5 = 2 клиента.

Вероятности того, что 0, 1, 2, 3 клиента прибудут за 5 мин, найдем по фор­муле, описывающей вероятность поступления заявок в систему (т.е. по закону Пуассона):

Вероятность того, что в течение 5 мин прибудут более 3 клиентов, равна 1 - [р(0) +р(1) +р(2) +р(3)] = 1 – (0,135 + 0,27 + 0,27 + 0,18) = 0,145.

Вероятность того, что фактическое время обслуживания заявки t не превы­сит заданной величины t, подчинена экспоненциальному закону и может быть определена по формуле р(t < t) = 1 – e^–tm, где средний темп обслуживания m = 0,6 клиента в минуту:

а) вероятность того, что время обслуживания не превысит 1 мин, р(t < 1) = 1 – e^–0,6×1 = 0,45;

б) вероятность того, что время обслуживания не превысит 2 мин, р(t < 2) = 1 – e^–0,6×2 = 0,70;

в) вероятность того, что время обслуживания составит более 2 мин, равна 1 – р(t < 2) = 0,30.

Вероятность того, что прибывающему клиенту придется ждать обслуживания,

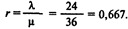
Вероятность того, что в системе находится п клиентов, можно найти, исполь­зуя предельные вероятности одноканальной системы с неограниченной очередью:

а) 0 клиентов:

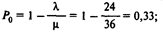
б) 3 клиента: P₃= r³•Р₀ = (0,667)³•0,33 = 0,098;

в) более 3 клиентов: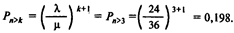

Ответы: 1. Два клиента. 2. 0,135; 0,27; 0,27; 0,18.

3. 0,145. 4. а) 0,45; 6) 0,7; в) 0,3.

5. 0,067. 6. а) 0,33; 6) 0,098; в) 0,198.

Задача 2. Решение.

Используем пакет POMWIN. Заполним модель М/М/1 исходными данными.

Для первого механика l = 2 клиента в час, m = 3 клиента в час, С_мех = 7 долл /ч; С_ож =15долл./ч:

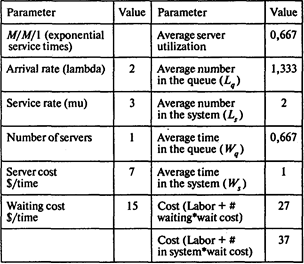
Среднее время, которое клиент проводит в очереди, W_q = 0,667 ч;

средняя длина очереди L_q = 1,333;

среднее время, которое клиент проводит в системе обслуживания, W_s = 1 ч;

среднее число клиентов в системе обслуживания L_s = 2;

вероятность того, что система обслуживания окажется свободной, равна 1 – r = 1 – 0,667 = 0,333.

Совокупные издержки по ожиданию в очереди и оплате первому механику равны 27 долл. в час.

Для второго механика l = 2 клиента в час, m = 4 клиента в час, С_мех = 10 долл./ч, С_ож = 15долл./ч:

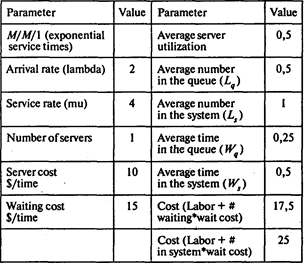
Среднее время, которое клиент проводит в очереди, W_q = 0,25 ч;

средняя длина очереди L_q = 0,5;

среднее время, которое клиент проводит в системе обслуживания, W_s = 0,5 ч;

среднее число клиентов в системе обслуживания L_s = 1;

вероятность того, что система обслуживания окажется незанятой равна 1–r = 1–0,5 = 0,5.

Совокупные издержки по ожиданию в очереди и оплате второму механику равны 17,5 долл. в час.

По результатам расчетов можно сделать вывод, что следует нанять второго механика.

Ответы: 1. Второго механика. 2. 17,5 долл./ч.

Задача 3. Решение.

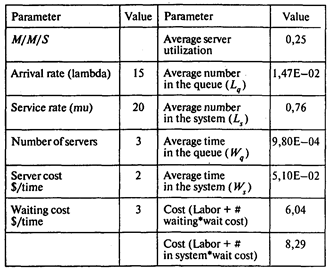
Заполним модель М/М/1 с одним продавцом (он же является кассиром) (l = 15 покупателей в час, m = 20 покупателей в час):

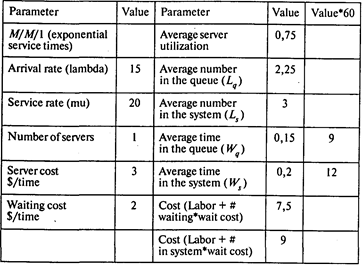
Среднее время, которое покупатель проводит в очереди, W_q = 0,15 ч = 9 мин;

средняя длина очереди L_q = 2,25;

среднее время, которое покупатель проводит в магазине W_s = 0,2 ч = 12 мин;

среднее число покупателей в магазине L_s = 3;

вероятность того, что в магазине не окажется покупателей, Р₀ = 1 – r = 1 – 0,75 = 0,25.

Если нанять продавца, который бы выполнял заказ, в то время как кассир рассчитывается с покупателем (альтернатива А), увеличится темп обслуживания клиентов (m = 30 покупателей в час), система останется одноканальной. Исполь­зуем для решения этой задачи модель М/М/1:

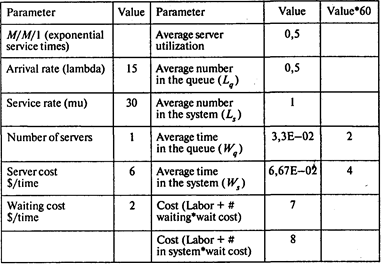
Среднее время, которое покупатель проводит в очереди, в этом случае сокра­тилось до W_q = 2 мин, издержки по ожиданию в очереди и обслуживанию канала сократились до 7 долл. в час.

Если нанять второго кассира, тем самым создав в магазине двухканальную очередь (альтернатива В), темп обслуживания на каждом канале будет равен m = 20 покупателей в час. Используем для решения этой задачи модель M/M/S:

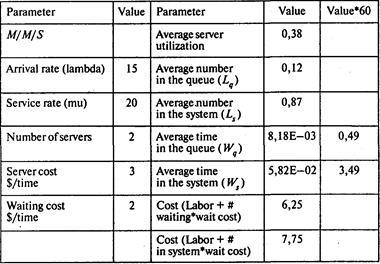
Среднее время, которое покупатель проводит в очереди, в этом случае сокра­тилось до W_q = 0,49 мин, издержки сократились до 6,25 долл. в час. Последний вариант более экономичен.

Ответ: Альтернативу В.

Задача 4. Решение. Заполним модель М/М/1:

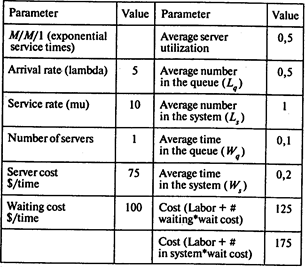
Вероятность того, что док будет пуст, Р₀ = 1 – 0,5 = 0,5;

среднее число судов в очереди L_q = 0,5;

среднее время ожидания обслуживания W_q = 0,1 ч = 6 мин;

среднее время пребывания в доке W_s = 0,2 ч = 12 мин.

Построим двухканальную систему обслуживания:

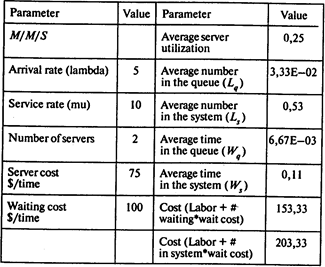
Степень загрузки системы сократилась до 0,25, совокупные издержки увели­чились на 28 долл. в час (203 - 175 = 28). Необходимости в строительстве второ­го дока нет.

Ответы: 1. 0,5. 2. 0,5 судна. 3. 6 мин. 4. 12 мин. 5. Нет необходимости.

Задача 5. Решение. Используем модель M/M/1:

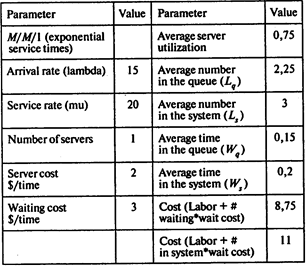
Если приобрести второй кассовый аппарат, создав в магазине двухканальную очередь, издержки сокращаются на 4,38 долл. в час (8,75 — 4,37 = 4,38):

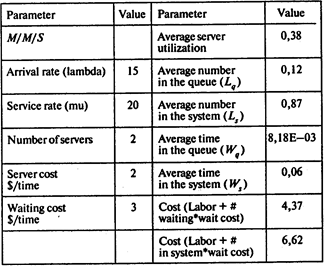
Включение третьего кассового аппарата ведет к увеличению издержек, поэтому нет необходимости в его приобретении:

Ответы: 1. Да, есть. 2. Нет необходимости.

Задача 6. Решение.

А. Заполним модель М/М/1 (l = 24 машины в час, m = 60/2 = 30 машин в час); одновременно заполним издержки по обслуживанию канала, включая оплату слу­жащего, и издержки по простою клиентов в очереди:

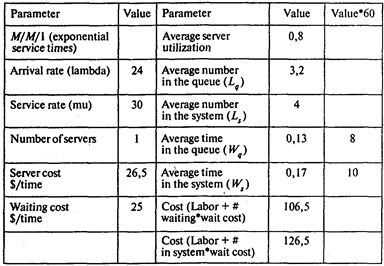
Вероятность того, что в системе нет машин, Р₀ = 1 – 0,8 = 0,2;

среднее число машин в очереди L_q = 3,2;

среднее время ожидания обслуживания W_q = 8 мин;

среднее время пребывания в системе W_s = 10 мин;

среднее число машин в системе L_s = 4;

вероятность того, что вновь прибывшей машине придется ждать, Р_n>0 = 0,8.

В. Используем модель М/М/1 (l = 24 машины в час, m = 60/1,25 = 48 машин в час):

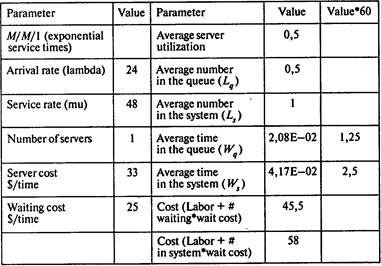
Вероятность того, что в системе нет машин, Р₀ = 1 – 0,5 = 0,5;

среднее число машин в очереди L_q = 0,5;

среднее время ожидания обслуживания W_q =1,25 мин;

среднее время пребывания в системе W_s = 2,5 мин;

среднее число машин в системе L_s= 1;

вероятность того, что вновь прибывшей машине придется ждать, Р_n>0 = 0,5.

С. Используем модель M/M/S (l = 24 машины в час, m = 60/2 = 30 машин в час):

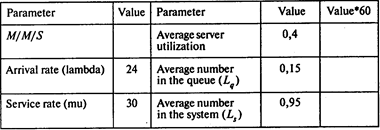
Окончание таблицы

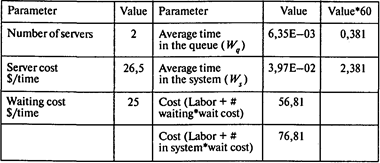
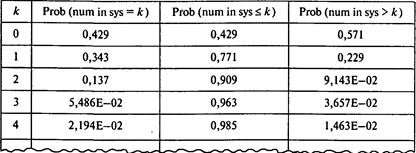
Вероятность того, что в системе нет машин, Р₀ = 0,43;

среднее число машин в очереди L_q = 0,15;

среднее время ожидания обслуживания W_q = 0,381 мин;

среднее время пребывания в системе W_s = 2,381 мин;

среднее число машин в системе L_s = 0,95;

вероятность того, что вновь прибывшей машине придется ждать, Р_n>0 = 0,57.

Часовые издержки по обслуживанию каналов и простою клиентов в очере­ди в первом случае составляют 106,5 долл., во втором — 45,5 долл., в третьем — 56,81 долл. Можно сделать вывод, что вариант B для фирмы требует меньших затрат.

Ответ: Вариант В.

Задача 7. Решение.

При использовании одноканальной модели каждый механик находится в системе 4 мин. Определим темп обслуживания клиентов m, если 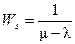= 4 мин и l = 4 клиента в минуту. Темп обслуживания для одноканальной системы равен m = 4,25 клиента в минуту:

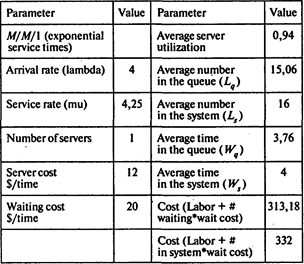
Среднее число клиентов в системе L_s = 16;

среднее время обслуживания одного клиента в системе равно W_s – W_q = 0,23 мин;

среднее число клиентов в очереди L_q = 15,06.

Построим двухканальную систему:

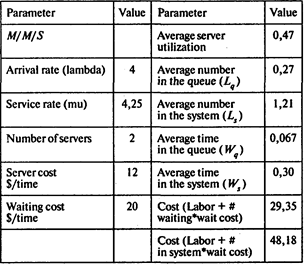
Среднее число клиентов в системе L_s = 1,2;

среднее время обслуживания одного клиента в системе равно W_s – W_q = 0,23 мин;

среднее числоклиентов в очереди L_q = 0,27.

В одноканальной модели издержки по ожиданию и обслуживанию выше из­держек двухканальной модели на 283,83 руб. в минуту (313,18 — 29,35 = 283,83).

Ответ: Двухканальная система.

Задача 8. Решение.

Используем модель M/D/1:

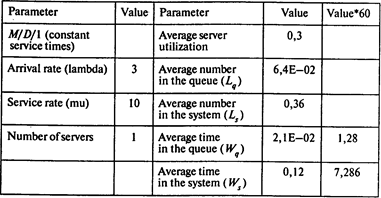
Среднее число автомобилей в очереди L_q = 0,064;

среднее время ожидания W_q = 1,28 мин;

в течение 30% рабочего времени система занята.

Ответы: 1. 0,064 автомобиля. 2. 1,28 мин. 3. 30% рабочего времени.

Задача 9. Решение.

Заполним модель M/M/S для случая работы одного механика:

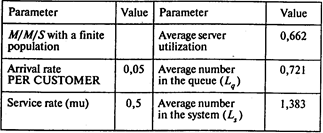
Окончание таблицы

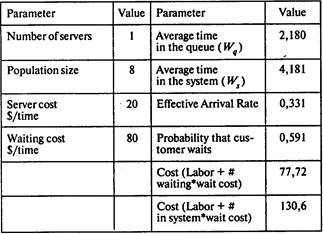
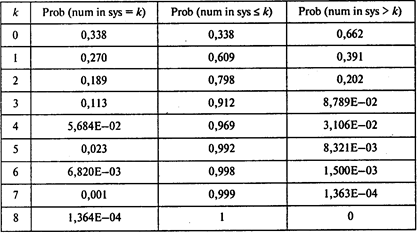
Вероятность того, что все машины работают и механик простаивает, Р₀ = 0,338;

среднее число ожидающих ремонта машин L_q = 0,721;

среднее число машин в системе L_s = 1,383;

среднее время ожидания начала ремонта W_q = 2,18 ч;

среднее время нахождения в системе (ожидание и ремонт) W_s = 4,181 ч.

Если нанять второго механика, получим

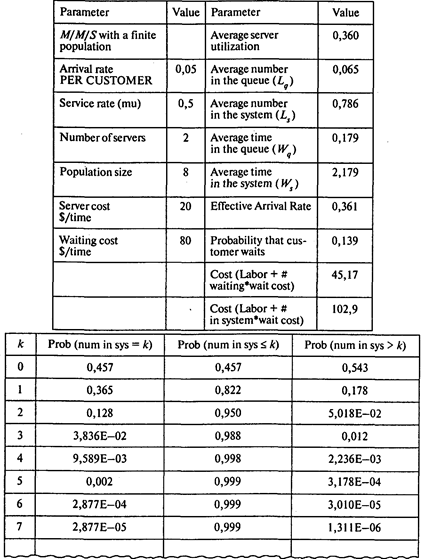
Вероятность того, что все машины работают и механик простаивает, Р₀ = 0,457;

среднее число ожидающих ремонта машин L_q = 0,065;

среднее число машин в системе L_q = 0,786;

среднее время ожидания начала ремонта W_q = 0,179 ч;

среднее время нахождения в системе (ожидание и ремонт) W_s = 2,179 ч.

С экономической точки зрения выгоднее нанять двух механиков.

Ответ: Двух механиков.

Задача 10. Решение.

Используем модель с ограниченной популяцией:

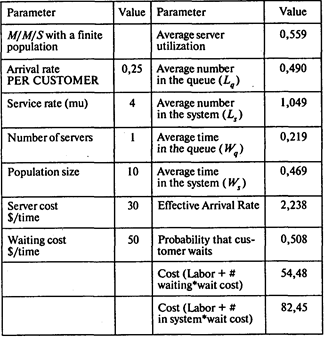
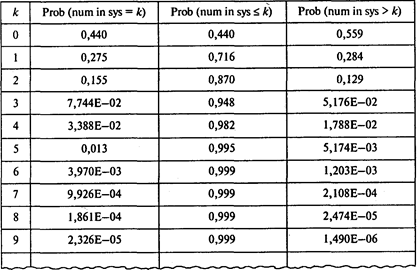
Вероятность того, что ни один грузовик не ожидает погрузки-разгрузки, Р₀= 0,44;

среднее число грузовиков в очереди L_q = 0,490;

среднее число грузовиков у магазина L_s = 1,049;

среднее время ожидания W_q = 0,219 ч = 13 мин;

Издержки по функционированию системы равны 54,48 долл. в час.

Ответ: 54,48 долл.

Глава 14. Имитационное моделирование

Цели

Имитация — это попытка дублировать особенности, внешний вид и характеристики реальной системы. Идея имитации реали­зуется следующим образом:

1) математическое описание реальной ситуации;

2) изучение ее свойств и особенностей;

3) формирование выводов и принятие решений, связанных с воздействием на эту ситуацию и основанных на результатах имитации.

Важно, что реальная система не подвергается воздействию до тех пор, пока преимущества или недостатки тех или иных управ­ленческих решений не будут оценены с помощью модели этой системы.

После того как вы выполните задания, предлагаемые в этой главе, вы. будете уметь использовать для экономического ана­лиза:

• имитацию;

• интервал случайных чисел;

• метод Монте-Карло;

• таблицу случайных чисел.

Модели

Метод Монте-Карло (метод статистических испытаний) состо­ит из четырех этапов:

1. Построение математической модели системы, описывающей зависимость моделируемых характеристик от значений стохасти­ческих переменных.

2. Установление распределения вероятностей для стохастичес­ких переменных.

3. Установление интервала случайных чисел для каждой сто­хастической переменной и генерация случайных чисел.

4. Имитация поведения системы путем проведения многих ис­пытаний и получение оценки моделируемой характеристики си­стемы при фиксированных значениях параметров управления. Оценка точности результата.

Описание этапов:

Первый этап. Стохастическая имитационная модель (ИМ) не­которой реальной системы может быть представлена как динами­ческая система, которая под воздействием внешних случайных входных сигналов (входных переменных) изменяет свое состояние (случайные переменные состояния), что в свою очередь приводит к изменению выходных сигналов (выходных переменных):

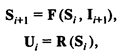
гдеF, R — вектор-функции;

I_i, U_i, S_i — векторы соответственно входных, выходных пере­менных и переменных состояния системы в так­товый момент моделирования i.

Имитационная модель — это экспериментальная модель систе­мы, в которой искусственно воспроизводятся случайности, име­ющие место в реальной системе. Она представляет собой совокуп­ность математических соотношений между входными, выходными переменными и переменными состояния в сочетании с алгорит­мической реализацией некоторых зависимостей.

Существует два подхода в имитационном моделировании ди­намических процессов.

Первый заключается в том, что весь период моделирования разбивается на равные промежутки времени (такты моделирова­ния) и анализ состояния системы, а также значений выходных переменных производится через одинаковые промежутки време­ни. При таком подходе возникает проблема выбора «правильной» продолжительности такта. Кроме того, не исключается появление тактов, в которых состояние системы по сравнению с предыдущим не изменилось.

При втором подходе величина такта моделирования не фик­сируется, моделирование в этом случае происходит в момент на­ступления одного из «существенных» событий. Например, при моделировании производственного процесса на предприятии та­кими событиями могут быть освобождение или начало загрузки станка, поступление на обработку детали, невыход на работу ста­ночника, исчерпание запаса необходимых комплектующих дета­лей на складе и др. Именно второй подход чаще всего использу­ется на практике и поддерживается современными языками мо­делирования.

Второй этап. Случайные величины, используемые в ИМ, мо­гут быть дискретными или непрерывными. В первом случае не­обходимо знать их распределения, во втором — плотности распре­делений. Эти зависимости могут быть известны из теории, опре­делены в результате специальных исследований либо заданы в качестве гипотезы. Точность модели (при прочих равных услови­ях) зависит от того, насколько точно заданы указанные распреде­ления (плотности распределений).

Третий этап. Моделирование случайных величин при компью­терных имитационных экспериментах производится с помощью датчика псевдослучайных чисел, предусмотренного в любом со­временном языке программирования. Обычно это датчик случай­ных чисел с равномерным распределением на интервале [0, 1]. Если известны вероятности наступления событий, то, используя такой датчик, можно отвечать на вопросы: «Какое из N возмож­ных событий произошло?» или «Какое значение приняла случай­ная величина?»

Предположим, что в ИМ используется случайная величина X, принимающая дискретные значения х₁, х₂,..., х_N с вероятностями соответственно p₁, p₂,..., p_N ( 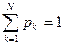). Получение некоторой реализации этой переменной в модели производится следующим образом.

Строится функция распределения случайной величины X. Ука­занная функция определяется посредством равенства F(X) = åp_k, в котором суммирование распространяется на все индексы, для которых х_k < X. С помощью датчика случайных чисел получают случайное число и из отрезка [0, 1].

Из равномерности распределения получаемых случайных чи­сел следует, что вероятность получения случайного числа из про­извольного интервала, включенного в [0, 1], равна длине этого интервала. Поэтому вероятность реализации Х = х_k равна веро­ятности попадания полученного от датчика случайного числа и в произвольный интервал длиной p_k на отрезке [0, 1]. Можно, та­ким образом, утверждать, что если очередное число и датчика удовлетворяет неравенствам 0 < и £ р₁, то имеет место реализа­ция Х = х₁, в случае p₁ < и £ p₁ + р₂ — реализация Х = х₂ и т.д. 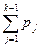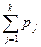В общем случае для k = 2, ..., N: если < и £ , то Х = х_k.

Заметим, что границы указанных неравенств совпадают со зна­чениями построенной выше функции распределения F(X).

Удобнее, однако, иметь дело не с дробными значениями гра­ниц интервалов, в которые попадает случайное число и, а с их целочисленными значениями, тем более, что с помощью датчи­ков случайных чисел можно генерировать числа из любого диа­пазона. Чтобы получить целые значения границ интервалов, до­статочно умножить все p_k на 10^d, где d — целое, минимальное зна­чение которого равно максимальной точности (максимальному числу знаков после десятичной точки) чисел p_k, k = 1,..., N. На­пример, если {р_k} = {0,3; 0,153; 0,5; 0,047}, то минимальное зна­чение d равно 3 (все р_k нужно умножить на 1000). Таким образом, 10^d определяет длину интервала значений рассматриваемой слу­чайной величины в ИМ.

Четвертый этап. Точность статистических оценок параметров реальной системы зависит от числа наблюдений (объема выбор­ки). Погрешности в оценках обусловлены как статистическим характером самой модели, так и влиянием начальных данных (на­чального состояния имитационной системы), а также возможной автокорреляцией последовательных значений некоторого парамет­ра в процессе моделирования. Очевидно, что с увеличением чис­ла испытаний точность моделирования должна возрастать. Ввиду того что увеличение объема выборки связано с ростом затрат на моделирование, важно уметь определять минимальное число ис­пытаний, необходимое для достижения заданной точности оцен­ки с заданной вероятностью.

Широкое распространение получили два метода статистичес­ких испытаний. Один из них предполагает проведение достаточ­но большого числа Т последовательных наблюдений в течение одного прогона модели (одного сеанса имитирования).

Другой метод заключается в реализации т независимых про­гонов модели, т.е. в m-кратном повторении одного и того же цикла имитирования. При этом, если мы хотим получить в сумме Т наблюдений, в течение каждого прогона можно делать по Т/т (допустим, что это число целое) наблюдений. Оба метода дают примерно одинаковый результат.

Пусть значения у_t (t = 1,..., Т) представляют собой результа­ты Т последовательных измерений значений случайной величи­ны y во время одного и того же сеанса имитации. Среднее по вре­мени значение у определяется выражением

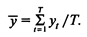
Обозначим через m математическое ожидание случайной вели­чины у. Тогда для достаточно большого T получаем