Открытая транспортная задача. 2 страница

Фирма «Мечта автомобилиста» использует прогнозы спроса для планирования объемов производства. При составлении плана про­изводства фирма должна учесть издержки найма или увольнения рабочих, оплату сверхурочных, субподряда, издержки хранения готовой продукции.

Издержки хранения составляют 0,12 руб. за 1 кг в неделю. Со­гласно смете производственные издержки в настоящее время рав­ны 20 руб. за 1 кг в неделю. Сумма затрат на каждого нанимаемо­го рабочего, приходящаяся на 1 кг продукции, составляет 5,63 руб. (данные издержки рассчитываются на основе затрат на обучение и средней производительности труда одного рабочего). Сумма за­трат на каждого увольняемого, приходящаяся на 1 кг продукции, составляет 15,73 руб. (рассчитывается исходя из размера компен­сационных выплат при увольнении и с учетом уменьшения пре­стижа фирмы). При нормальном режиме работы (без сверхуроч­ных) фирма может производить до 1900 кг стекла в неделю. Кро­ме того, может быть произведено до 100 кг при использовании субподряда, и еще 250 кг стекла в неделю «Мечта автомобилиста» может произвести на своих мощностях сверхурочно. Издержки для стекла, производимого сверхурочно, на 8 руб. за 1 кг больше, чем для производимого в обычное время. Издержки производства по субподряду на 2 руб. за 1 кг больше, чем при производстве сверх­урочно (т.е. на 10 руб. за 1 кг выше, чем при производстве в обыч­ном режиме).

В настоящее время запасы стекла на складе составляют 73 кг. Производство работает на полную мощность, выпуская 1900 кг продукции в неделю.

Задание

Составьте агрегированный план производства для фирмы «Мечта автомобилиста» в целях минимизации совокупных из­держек. Примите во внимание различные предположения и ва­рианты реализации производственной политики и покажите, как эти различия отразятся на вариантах планов.

Ответы и решения

Ответы на вопросы: 1—1, 2 — 2, 3—2, 4 — 1, 5—4.

Задача 1. Решение.

С учетом исходной информации транспортная таблица имеет вид

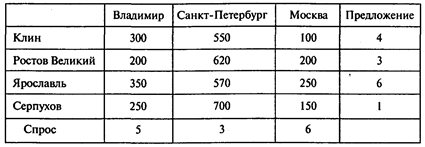
Результаты расчетов (оптимальный план доставки автомобилей):

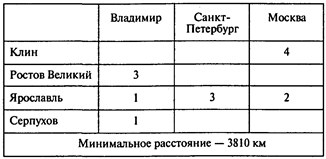
С учетом дополнительной информации транспортная таблица имеет вид

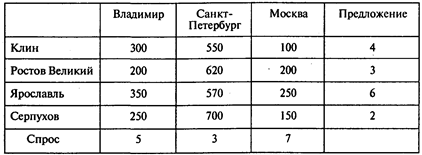
Оптимальный план доставки автомобилей:

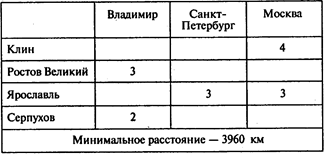
Ответы: 1. 3810 км. 2. Два автомобиля. 3. На 150 км.

Задача 2. Решение.

Транспортная таблица имеет вид

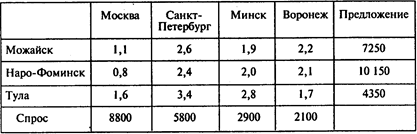
Результаты расчетов (оптимальный план транспортировки стульев):

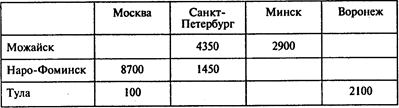
С учетом запретов на перевозки имеем следующую транспортную таблицу, где М — большое число:

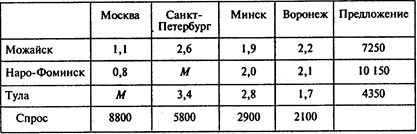
С учетом дополнительных ограничений на перевозки модель имеет вид

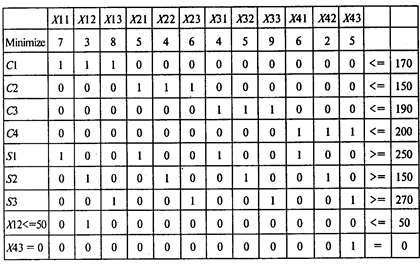
Результаты расчетов:

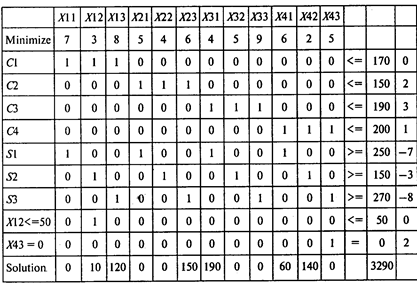
Ответы: 1. 130 тыс. т. 2. 180 тыс. т. 3. 2930 тыс. руб. 4. На 360 тыс. руб. 5. 140 тыс. т.

Задача 4. Решение.

Транспортная таблица имеет вид (издержки производства в основное время принимаются равными нулю; буква M означает запрет соответствующих «пере­возок»)

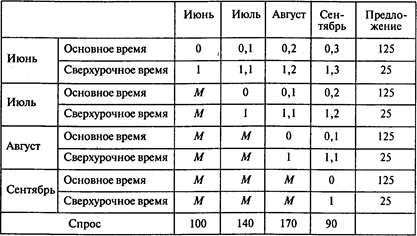
Результаты расчетов:

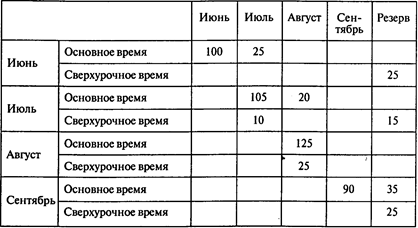
Ответы: 1. 125 ящиков. 2. 0 часов.

Задача 5. Решение.

Транспортная таблица имеет вид

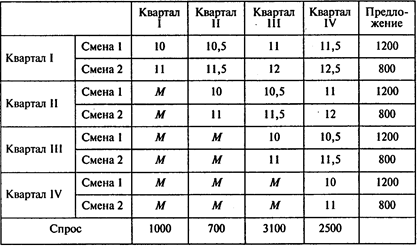
План производства:

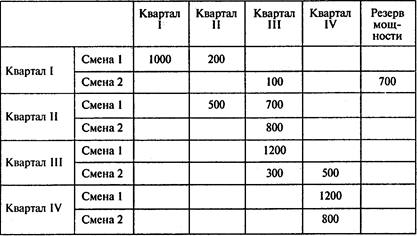
Ответы: 1. 1300 компьютеров. 2. На 12,5%. 3. 2000 компьютеров. 4. 800 компьютеров. 5. 76700 тыс. руб.

Глава 6. Задача о назначениях

Цели

В процессе управления производством зачастую возникают за­дачи назначения исполнителей на различные виды работ, напри­мер: подбор кадров и назначение кандидатов на вакантные долж­ности, распределение источников капитальных вложении между различными проектами научно-технического развития, распреде­ление экипажей самолетов между авиалиниями.

Задачу о назначениях можно сформулировать следующим об­разом. Необходимо выполнить N различных работ. Для их выпол­нения можно привлечь N рабочих. Каждый рабочий за определен­ную плату готов выполнить любую работу. Выполнение любой работы следует поручить одному рабочему. Требуется так распре­делить работы между рабочими, чтобы общие затраты на выпол­нение всех работ были минимальными.

После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь определять и использовать для экономи­ческого анализа:

• задачу о назначениях в стандартной форме;

• открытую задачу о назначениях;

• таблицу задачи о назначениях;

• матрицу назначений;

• эффективность назначений.

Модели

Пусть т — количество работ.

Задача о назначениях в стандартной форме. При рассмотрении задачи о назначениях в стандартной форме предполагается, что количество рабочих равно количеству работ.

Обозначения:

с_ij — показатель эффективности назначения i-го рабочего на j-й работе, например издержки выполнения i-м рабочим j-й работы;

x_ij — переменная модели (х_ij = 1, если i-й рабочий использует­ся на j-й работе, и x_ij = 0 в противном случае).

Модель задачи о назначениях:

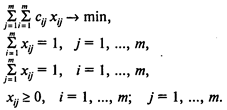
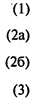
Здесь (1) — целевая функция (минимум издержек на выполнение всех работ);

(2) — система ограничений, отражающая следующие усло­вия:

а) каждая работа должна быть выполнена одним рабо­чим;

б) каждый рабочий может быть привлечен к одной работе;

(3) — условия неотрицательности переменных.

При решении задачи о назначениях исходной информацией является таблица задачи о назначениях с={с_ij}, элементами ко­торой служат показатели эффективности назначений. Для задачи о назначениях, записанной в стандартной форме, количество строк этой таблицы совпадает с количеством столбцов:

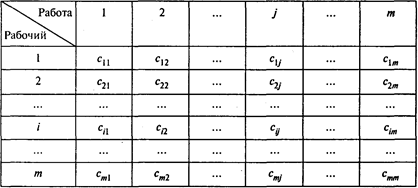
Результатом решения задачи о назначениях (1)—(3) является вектор х* = { 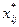}, компоненты которого — целые числа.

Оптимальный план задачи о назначениях (1)—(3) можно пред­ставить в виде квадратной матрицы назначений, в каждой строке и в каждом столбце которой находится ровно одна единица. Та­кую матрицу иногда называют матрицей перестановок. Значение целевой функции (1), соответствующее оптимальному плану, на­зывают эффективностью назначений.

Задача о назначениях в открытой форме. Задача о назначени­ях в открытой форме возникает тогда, когда количество рабочих не равно количеству работ. В этих случаях задача может быть пре­образована в задачу, сформулированную в стандартной форме.

Пусть, например, количество рабочих п превышает количество работ т.

Введем дополнительные фиктивные работы с индексами j = w + 1,..., п. Коэффициенты таблицы назначений с_ij , i = 1,..., п; j = т + 1,..., п, положим равными нулю. В этом случае получаем задачу, сформулированную в стандартной форме. Если в опти­мальном плане этой задачи 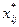= 1 при j = т + 1,..., п, то испол­нитель i назначается на выполнение фиктивной работы, т.е. ос­тается без работы. Заметим, что оптимальное значение целевой функ­ции исходной задачи совпадает с оптимальным значением задачи, приведенной к стандартной форме. Поэтому эффективность на­значений в результате такого преобразования не меняется.

Следует особо отметить, что задача о назначениях является частным случаем транспортной задачи, в которой количество пунк­тов производства совпадает с количеством пунктов потребления, а все величины спроса и величины предложения равны.

Примеры

Пример 1. Распределение работ.

Фирма получила заказы на разработку пяти программных про­дуктов. Для выполнения этих заказов решено привлечь пятерых наиболее опытных программистов. Каждый из них должен напи­сать одну программу. В следующей таблице приведены оценки времени (в днях), необходимого программистам для выполнения каждой из этих работ:

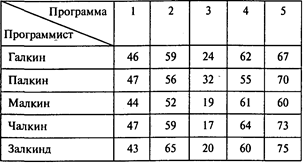
Оценки даны самими программистами, и у фирмы нет осно­вания им не доверять.

Распределите работы между программистами, чтобы общее ко­личество человекодней, затраченное на выполнение всех пяти за­казов, было минимальным.

Вопросы:

1. Какое минимальное количество человекодней необходимо для выполнения всех пяти заказов?

2. Какую программу следует поручить Малкину?

3. Какую программу следует поручить Залкинду?

Решение. Таблица задачи о назначениях представлена в усло­вии. Проведя расчеты, получаем следующую матрицу назначений:

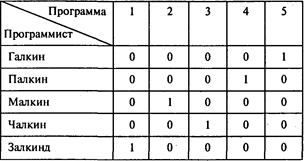
Учитывая исходную информацию, получаем следующий ре­зультат:

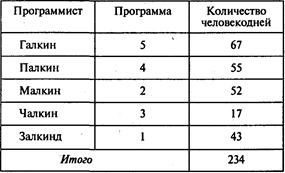
Ответы: 1. 234 человекодня. 2. Программу 2. 3. Программу 1.

Вопросы

Вопрос 1. Задача о назначениях относится к классу задач:

1) линейного программирования;

2) эконометрических;

3) статистических;

4) имитационных;

5) не относится ни к одному из указанных классов.

Вопрос 2. Имеются две работы r₁, r₂, и два рабочих L₁ , L₂, каж­дый из которых может выполнить любую работу. Элемент a_ij мат­рицы А показывает время, необходимое рабочему i для выполне­ния работы j:

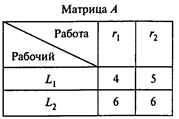
Решите задачу о назначениях. Чему равно минимальное время выполнения двух работ?

Варианты ответов:

1) 9; 2) 10; 3) 11; 4) 12; 5)13.

Вопрос 3. Как известно, задача о назначениях является част­ным случаем транспортной задачи. Какая из приведенных ниже характеристик транспортной таблицы, построенной для задачи о назначениях, наиболее правильная?

Варианты ответов:

1) объемы потребления равны единице, объемы поставок от­личны от единицы;

2) объемы поставок равны единице, объемы потребления от­личны от единицы;

3) матрица транспортных затрат квадратная, объемы поставок отличны от единицы;

4) матрица транспортных затрат квадратная, объемы потребле­ния отличны от единицы;

5) матрица транспортных затрат прямоугольная, объемы поста­вок равны единице.

Вопрос 4.Оптимальный план задачи о назначениях можно представить в виде:

1) квадратной матрицы, в каждой строке которой находится одна единица;

2) квадратной матрицы, в каждом столбце которой находится одна единица;

3) квадратной матрицы, в каждой строке и в каждом столбце которой находится одна единица;

4) квадратной матрицы, в каждой строке которой находится хотя бы одна единица;

5) квадратной матрицы, в каждом столбце которой находится хотя бы одна единица.

Вопрос 5. Имеются две работы r₁, r₂ и трое рабочих L₁, L₂ и L₃, каждый из которых может выполнить любую работу. Элемент а_ij матрицы А показывает время, необходимое рабочему i для выпол­нения работы j:

Решите задачу о назначениях. Чему равно минимальное время выполнения двух работ?

Варианты ответов:

1) 5; 2) 6; 3) 7; 4) 8; 5) 9.

Задачи

Задача 1. Цех металлообработки получил срочный заказ на выпуск партии деталей. Для производства детали необходимо выполнить операции на четырех станках. В цехе работают четыре слесаря высокой квалификации, каждый из которых может рабо­тать на любом станке, но с различным процентом брака (процент брака известен из документации ОТК):

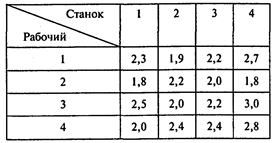
Распределите станки между рабочими таким образом, чтобы процент брака был минимальным. (Предполагается, что ОТК про­веряет готовую деталь, т.е. общий процент брака определяется как сумма процентов брака, допущенного всеми рабочими.)

Вопросы:

1. На каком станке должен работать рабочий 2?

2. Чему равен минимальный общий процент брака?

Задача 2. Воронежская фирма по производству мужских голов­ных уборов планирует освоение новых рынков сбыта в пяти го­родах. Возможности сбыта невелики, так что в каждый город до­статочно направить одного торгового представителя фирмы для заключения с магазинами договоров о поставках.

В следующей таблице указан объем спроса (в млн руб.):

Фирма располагает данными о профессиональных возможно­стях шести своих сотрудников. В следующей таблице содержатся оценки степени освоения рынка, которую может обеспечить со­ответствующий торговый представитель фирмы:

Так, представитель П₁ может освоить 70% от объема спроса в любом городе. Например, если направить его в Москву, то доход фирмы на этом рынке составит 6,3 млн руб.

Распределите торговых агентов по городам таким образом, что­бы фирма получила максимальный доход.

Вопросы:

1. Чему равен максимальный доход фирмы?

2. В какой город следует направить торгового представи­теля П₁?

3. Кто из торговых представителей не будет использован?

Задача 3. Фирма получила заказы на разработку пяти про­граммных продуктов. На фирме работают шесть квалифицирован­ных программистов, которым можно поручить выполнение этих заказов. Каждый из них дал оценку времени (в днях), требуемого для разработки программ. Эти оценки приведены в следующей таблице:

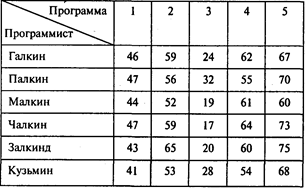
Выполнение каждого из пяти заказов фирма решила поручить одному программисту. Ясно, что один из программистов не по­лучит заказа.

Каждому программисту, которому будет поручено выполнять заказ, фирма предложила оплату 1 тыс. руб. в день. Распределите работу между программистами, чтобы общие издержки на разра­ботку программ были минимальными.

Вопросы:

1. Чему равны минимальные издержки фирмы на выполнение всех пяти заказов?

2. Какую программу следует поручить Малкину?

3. Какую программу следует поручить Залкинду?

4. Кто из программистов не получит заказа?

5. Стало известным, что не все программисты согласились с условиями оплаты, обосновывая это тем, что имеют разную квалификацию. В результате была достигнута договорен­ность о следующих размерах оплаты в день (в тыс. руб.):

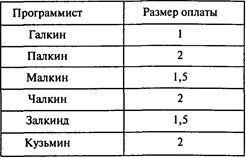
Изменится ли распределение работ между программистами при новых условиях оплаты труда? Каковы будут в этом слу­чае общие минимальные издержки? б. Кто из программистов при новых условиях не получит заказа?

Задача 4. Пять учебных групп экономического факультета МГУ собираются посетить во время практики 10 предприятии и НИИ. Каждая учебная группа может посетить две организации. Путем опроса студентов выявлены предпочтения каждой группы для 10 ор­ганизаций (1 означает «наиболее предпочтительна», а 10 — «наи­менее предпочтительна»). Предпочтения каждой из пяти учебных групп показаны в таблице (П-1 ¸ П-5 — промышленные предприя­тия; НИИ-1 ¸ НИИ-5 — научно-исследовательские институты):

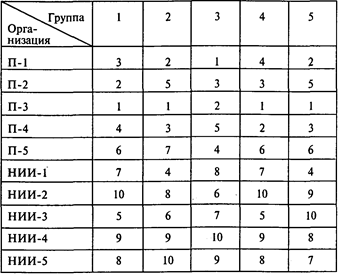
Определите, какие две организации должна посетить каждая группа, чтобы в максимальной степени были учтены предпочте­ния всех студентов.

Вопросы:

1. Чему равна сумма баллов, соответствующая наилучшему рас­пределению групп по организациям?

2. Какая группа должна посетить НИИ-2?

3. Какую еще организацию должна посетить эта группа?

4. Деканат внес предложение, чтобы каждая группа посетила одно предприятие и один НИИ. Укажите теперь такой ва­риант распределения, чтобы каждой группе досталось по одному промышленному предприятию и одному НИИ. Че­му равна сумма оценочных баллов в этом случае?

5. Какая группа должна посетить НИИ-5 при новых условиях?

6. Какую еще организацию должна посетить эта группа?

Задача 5. Самолеты компании «Аэрофлот» летают между Моск­вой и Сочи. Полеты беспосадочные. График движения показан в следующей таблице:

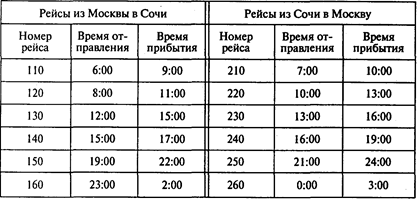
Рейсы могут обслуживаться московскими или сочинскими эки­пажами. Любой экипаж выполняет пару рейсов — «туда и обрат­но». Время, необходимое для подготовки самолета к очередному рейсу, — один час. Требуется определить, какую пару рейсов сле­дует выполнять каждому экипажу и из какого отряда, московско­го или сочинского, должен быть соответствующий экипаж. Рас­пределение рейсов необходимо осуществить таким образом, что­бы суммарное время ожидания вылета в «чужом» городе было минимальным. Время ожидания не включает тот час, который уходит на подготовку самолета к очередному рейсу.

Вопросы:

1. Верно ли, что рейс 210 должен выполняться московским экипажем?

2. Верно ли, что рейсы 240 и 160 должны выполняться одним экипажем?

3. Верно ли, что рейс 160 должен обслуживаться сочинским экипажем?

4. Каково минимальное общее время пребывания экипажей в «чужих» городах?

5. Какое количество рейсов должны выполнять московские экипажи?

Ответы и решения

Ответы на вопросы: 1—1, 2 — 2, 3—5, 4 — 3, 5 —3.

Задача 1. Решение.

Таблица задачи о назначениях представлена в условии. Проводя оптимизационные расчеты, получаем следующую матрицу назначений:

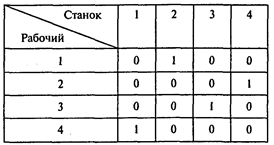
Решение можно представить в следующем виде:

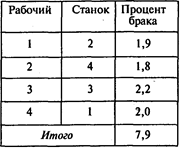
Ответы: 1. На станке 4. 2. 7,9%.

Задача 2. Решение.

Способ 1 (без проведения оптимизационных расчетов). Известно, что при любых неотрицательных а₁, b₁, а₂, b₂ соотношение а₁b₁ + а₂b₂ ³ а₂b₁ + а₁b₂ вы­полняется в случае, когда a₁ ³ а₂, и b₁ ³ b₂. Используя это утверждение, можно по­казать, что максимальный доход будет в том случае, когда торговый представи­тель, обеспечивающий максимальную долю освоения рынка, будет направлен в город с максимальным объемом спроса, и т.д.

Способ 2. В таблице задачи о назначениях указан размер дохода (в млн руб.), который можно получить при направлении представителя фирмы в соответству­ющий город:

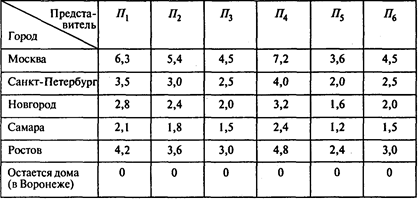
Проводя оптимизационные расчеты, получаем следующий результат:

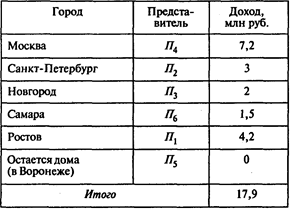
Ответы: 1. 17,9 млн руб. 2. В Ростов. 3. Представитель П₅.

Задача 3. Решение.

В таблице задачи о назначениях указан размер оплаты (в тыс. руб.) в случае, если программисту будет поручена соответствующая программа:

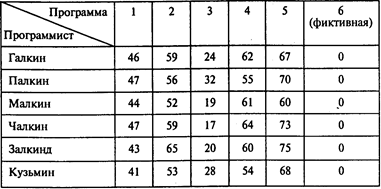
Проводя расчеты, получаем следующую матрицу назначений:

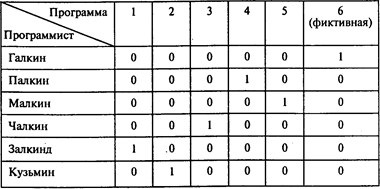
Учитывая исходную информацию, получаем следующий результат:

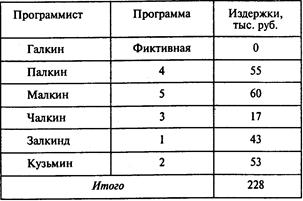
Из последней таблицы следует, что минимальные издержки составляют 228 тыс. руб., Малкину следует поручить программу 5, а Залкинду — программу 1. Заказа не получит Галкин.

При новых условиях оплаты труда таблица задачи о назначениях имеет сле­дующий вид:

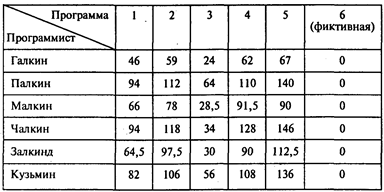
Проводя расчеты, получаем следующую матрицу назначений:

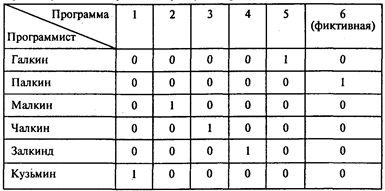
В следующей таблице приведен итоговый результат:

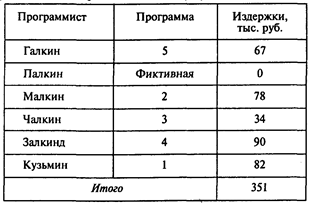
Ответы: 1. 228 тыс. руб. 2. Программу 5. 3. Программу 1. 4. Программист Галкин. 5. 351 тыс. руб.

6. Программист Палкин.

Задача 4. Решение.

В таблице задачи о назначениях указаны предпочтения каждой группы, при этом каждая группа представлена дважды, так как может посетить две организации:

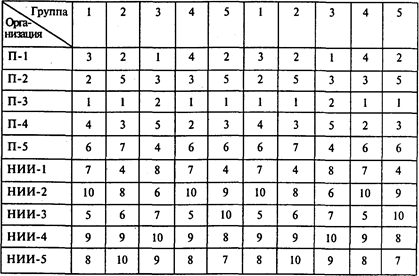
Проводя оптимизационные расчеты, получаем следующий результат:

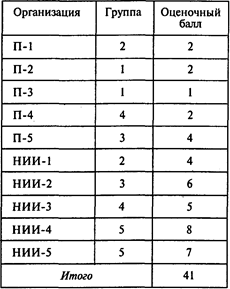
Если учесть предложение деканата, то надо решить две задачи о назначени­ях: сначала распределить группы по предприятиям, затем — по НИИ. Эти две за­дачи можно представить в виде одной оптимизационной задачи, имеющей сле­дующую таблицу (М— большое число):

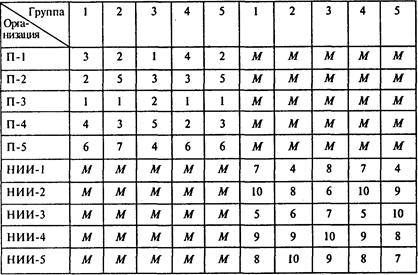
Минимизируя общую сумму баллов, получаем следующую матрицу назначений:

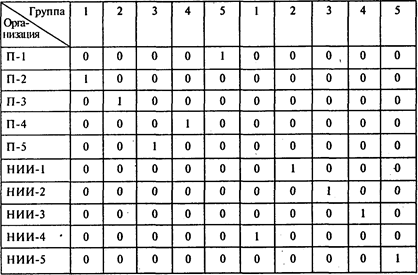
Ответ можно представить в виде следующей таблицы:

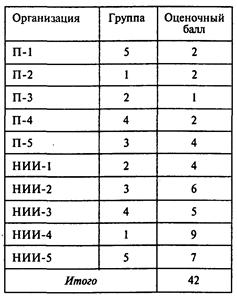
Ответы: 1. 41. 2. Группа 3. 3. Предприятие П-5. 4. 42. 5. Группа 5. 6. Предприятие П-1.

Задача 5. Решение.

Составляем таблицу задачи о назначениях, предполагая, что все рейсы выпол­няются московскими экипажами. Наименование столбца таблицы — номер рей­са «Москва — Сочи» (М — С). Наименование строки — номер обратного рейса «Сочи — Москва» (С — М). В таблице для каждой возможной пары рейсов, вы­полняемых одним экипажем, указано время ожидания вылета в Сочи (в часах):

Московский экипаж

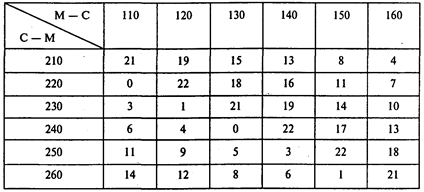
Составляем таблицу задачи о назначениях, предполагая, что все рейсы выпол­няются сочинскими экипажами. Наименование строки — номер рейса «Сочи — Москва». Наименование столбца — номер обратного рейса «Москва — Сочи». В таблице для каждой возможной пары рейсов, выполняемых одним экипажем, указано время ожидания вылета в Москве (в часах):

Сочинский экипаж

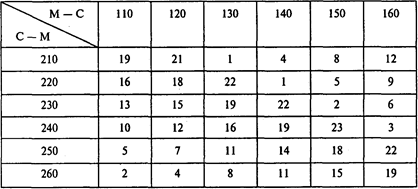
Составляем итоговую таблицу задачи о назначениях. Учитываем, что каждая пара рейсов может выполняться либо московским, либо сочинским экипажем. Поэтому в итоговую таблицу включаем минимальные значения времени ожида­ния (в часах) из двух приведенных выше таблиц:

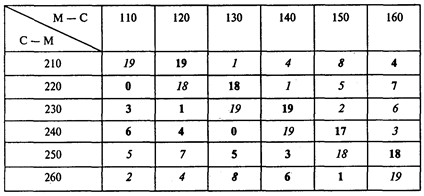
Элементы, выделенные полужирным шрифтом, взяты из таблицы для москов­ского экипажа. Соответствующие пары рейсов должны выполняться московским экипажем. Элементы, выделенные курсивом, взяты из таблицы для сочинского экипажа. Соответствующие пары рейсов должны выполняться сочинским экипа­жем. Элементы, выделенные полужирным курсивом, показывают, что соответ­ствующая пара рейсов может выполняться экипажем, приписанным к любому из двух городов.

Решая задачу, получаем следующую матрицу назначений:

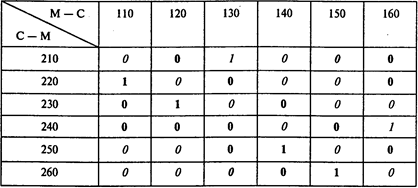
В матрице назначений единица, выделенная полужирным шрифтом, означа­ет, что соответствующая пара рейсов должна выполняться московским экипажем. Единица, выделенная курсивом, означает, что соответствующая пара рейсов долж­на выполняться сочинским экипажем.

В итоге получаем следующее решение задачи:

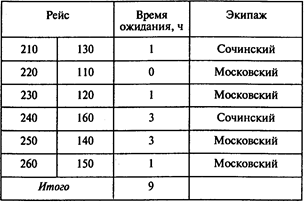
Ответы: 1. Нет, рейс 210 должен выполняться сочинским экипажем. 2. Да. 3. Да. 4. 9 часов. 5. Восемь рейсов.

Глава 7. Сетевой анализ проектов. Метод СРМ

Цели

В данной главе показаны возможности использования метода СРМ (Critical Path Method — метод критического пути) для конт­роля сроков выполнения проекта. Таким проектом может быть разработка нового продукта или производственного процесса, строительство предприятия, здания или сооружения, ремонт слож­ного оборудования и т.д.

При реализации проекта составляется график выполнения ра­бот. Для того чтобы проект был завершен вовремя, необходимо контролировать сроки выполнения этих работ. Усложняющим фактором является то, что работы взаимосвязаны. Одни работы зависят от выполнения других и не могут начаться, пока предшест­вующие работы не будут завершены.

Важной предпосылкой применения метода СРМ является пред­положение о том, что время выполнения каждой работы точно известно.

В результате использования метода СРМ удается получить от­веты на следующие вопросы:

1. За какое минимальное время можно выполнить проект?

2. В какое время должны начаться и закончиться отдельные работы?

3. Какие работы являются «критическими» и должны быть вы­полнены точно в установленное время, чтобы не был сорван срок выполнения проекта?

4. На какое время можно отложить срок выполнения «некри­тической» работы, чтобы она не повлияла на срок выполне­ния проекта в целом?

После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь определять и использовать для экономи­ческого анализа:

• наиболее раннее и наиболее позднее время начала работы;

• наиболее раннее и наиболее позднее время окончания работы;

• критический путь;

• длину критического пути;

• запас времени на выполнение работы.

Модели

Исходным шагом для применения метода СРМ является опи­сание проекта в виде перечня выполняемых работ с указанием их взаимосвязи. Для описания проекта используются два основных способа: табличный и графический.

Рассмотрим следующую таблицу, описывающую проект:

В первом столбце указаны наименования всех работ проекта. Их четыре: А, В, С, D. Во втором столбце указаны работы, непо­средственно предшествующие данной. У работ А и В нет предшест­вующих. Работе С непосредственно предшествует работа В. Это означает, что работа С может быть начата только после того, как завершится работа В. Работе D непосредственно предшествуют две работы: А и С. Это означает, что работа D может быть начата толь­ко после того, как завершатся работы А и С. В третьем столбце таблицы для каждой работы указано время ее выполнения. На основе этой таблицы может быть построено графическое описа­ние проекта (рис. 1).

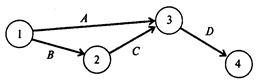
Рис. 1

На рис. 1 проект представлен в виде графа с вершинами 1,2, 3, 4 и дугами А, В, С, D. Каждая вершина графа отображает собы­тие. Событие 1 означает начало выполнения проекта. Иногда та­кое событие обозначают буквой s (start). Событие 4 означает за­вершение проекта. Для обозначения такого события иногда ис­пользуют букву f( finish). Любая работа проекта — это упорядочен­ная пара двух событии. Например, работа А есть упорядоченная пара событий (1, 3)(см. рис. 1). Работа D — упорядоченная пара событий (3,4). Событие проекта состоит в том, что завершены все работы, «входящие» в соответствующую вершину. Например, со­бытие 3 состоит в том, что завершены работы А и С.