Определение интенсивности использования рациональных способов раскроя.
Обозначения:
j —индекс материала, j = 1,..., п;
k —индекс вида заготовки, k = 1, ..., q;
i — индекс способа раскроя единицы материала, i = 1,..., р;
аijk — количество (целое число) заготовок вида k, полученных при раскрое единицы j-го материала i-м способом;
bk — число заготовок вида k в комплекте, поставляемом заказчику;
dj — количество материала j-го вида;
xji — количество единицу j-го материала, раскраиваемых по i-му способу (интенсивность использования способа раскроя);
cji — величина отхода, полученного при раскрое единицы j-го материала по i-му способу;
у — число комплектов заготовок различного вида, поставляемых заказчику.
Модель А раскроя с минимальным расходом материалов:
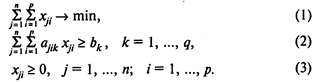
Здесь (1) — целевая функция (минимум количества используемых материалов);
(2) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;
(3) — условия неотрицательности переменных.
Специфическими для данной области приложения модели линейного программирования являются ограничения (2).
Модель В раскроя с минимальными отходами:
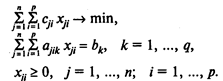
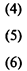
Здесь (4) — целевая функция (минимум отходов при раскрое материалов);
(5) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;
(6) — условия неотрицательности переменных.
Модель С раскроя с учетом комплектации:
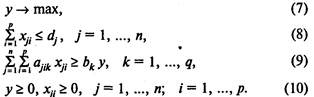
Здесь (7) — целевая функция (максимум комплектов, включающих заготовки различных видов);
(8) — ограничения по количеству материалов;
(9) — система ограничений, определяющих количество заготовок, необходимое для формирования комплектов;
(10) — условия неотрицательности переменных.
Специфическими для данной области приложения модели линейного программирования являются ограничения (9).
Примеры
Пример 1. Способы раскроя металлического стержня.
Определите все рациональные способы раскроя металлического стержня длиной 100 см на заготовки трех типов: длиной 20, 30 и 50 см. Укажите величину отходов для каждого способа.
Решение. Для данного материала и указанных заготовок существует семь различных рациональных способов раскроя. Все они приведены в следующей таблице:
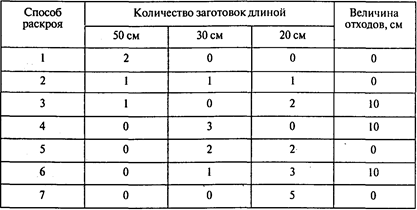
Пример 2. Способы раскроя куска кожи.
Определите все рациональные способы раскроя прямоугольного куска кожи размером 100 х 60 см на квадратные заготовки со сторонами 50,40 и 20 см и укажите величину отходов для каждого способа.
Решение. Для данного материала и указанных заготовок существует шесть различных рациональных способов раскроя:
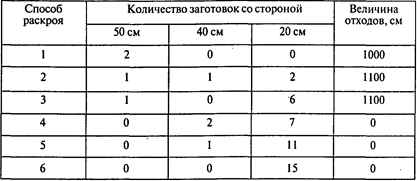
Пример 3. Изготовление парников из металлических стержней.
При изготовлении парников используется материал в виде металлических стержней длиной 220 см. Этот материал разрезается на стержни длиной 120, 100 и 70 см. Для выполнения заказа требуется изготовить 80 стержней длиной 120 см, 120 стержней длиной 100 см и 102 стержня длиной 70 см.
Вопросы:
1. Сколько существует рациональных способов раскроя?
2. Какое минимальное количество материала следует разрезать, чтобы выполнить заказ?
3. Сколько способов раскроя следует использовать при выполнении заказа?
Решение. Определяем все рациональные способы раскроя материала на заготовки. Таких способов оказывается пять:
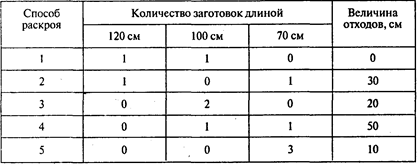
Используем модель А для одного вида материала. Тогда хi — количество единиц материала, раскраиваемых по i-му способу.
Для ответа на второй и третий вопросы задачи получаем следующую модель линейного программирования с критерием «минимум общего количества используемого материала»:
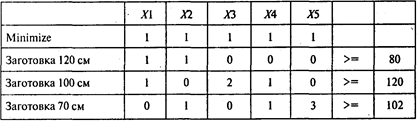
Решая задачу, получаем следующий результат:
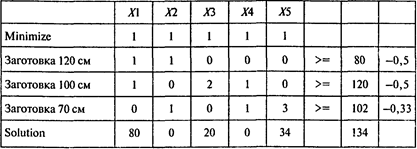
Ответы: 1. Пять способов. 2. 134 единицы материала. 3. Три из пяти рациональных способов раскроя.
Вопросы
Вопрос 1. Способ раскроя называется рациональным, если:
1) он является безотходным;
2) он обеспечивает минимум отходов;
3) отходы меньше любой из заготовок;
4) он позволяет получить наибольшее число заготовок;
5) нет другого способа, дающего не меньше заготовок каждого типа.
Вопрос 2. Рассматривается задача оптимального раскроя деревянных брусьев на заготовки для строительства дома. Длина брусьев измеряется в сантиметрах. В соответствующей модели линейного программирования неизвестными являются интенсивности рациональных способов раскроя материала, значения которых измеряется в штуках. В качестве критерия рассматривается минимум отходов. В каких единицах измеряется коэффициент целевой функции?
Варианты ответов:
1) шт.; 2) см; 3) шт./см; 4) см/шт.;
5) безразмерная величина.
Вопрос 3. Рассматривается задача оптимального раскроя кожи для пошива перчаток. В соответствующей модели линейного программирования учитывается ограничение на количество материала. Правая часть ограничения измеряется в штуках кожи. Максимизируется количество пар пошитых перчаток. В каких единицах измеряется двойственная оценка ресурсного ограничения?
Варианты ответов:
1) шт.; 2) пара; 3) пара/шт.; 4) шт./пара; 5) безразмерная величина.
Вопрос 4. Сколько существует рациональных способов раскроя металлического стержня длиной 100 см на стержни длиной 50, 20 и 10 см?
Варианты ответов:
1) более десяти; 2) десять; 3) девять;
4) восемь; 5) менее восьми.
Вопрос 5. Какое из следующих утверждений является верным?
Варианты ответов:
1) безотходный способ раскроя является рациональным;
2) безотходный способ раскроя может быть рациональным;
3) безотходный способ раскроя не является рациональным;
4) рациональный способ раскроя является безотходным;
5) рациональный способ раскроя не является безотходным.
Задачи
Задача 1. Из прямоугольного листа железа размером 100 х 60 см необходимо изготовить квадратные заготовки со сторонами 50,40 и 20 см. Эти заготовки нужны в качестве перегородок при изготовлении пластмассовых коробок для хранения инструментов. Чтобы сделать одну коробку, нужно иметь четыре заготовки со стороной 50 см, шесть заготовок со стороной 40 см и двенадцать — со стороной 20 см. На складе находится 100 листов материала.
Вопросы:
1. Сколько существует рациональных способов раскроя?
2. Какое максимальное количество коробок можно изготовить при условии, что оставшиеся заготовки можно использовать для следующей партии коробок?
3. Сколько рациональных способов раскроя следует использовать?
4. Сколько листов материала нужно, чтобы изготовить одну коробку?
Задача 2. Существует три рациональных способа раскроя единицы материала А на заготовки трех типов. Эти же заготовки могут быть получены двумя рациональными способами при раскрое единицы материала В. Количество заготовок, получаемых каждым из этих способов, показано в следующей таблице:

Заготовки используются для производства бытовой техники. В комплект поставки входят четыре заготовки первого типа, три заготовки второго типа и семь — третьего типа. На складе имеется 100 единиц материала А и 300 единиц материала В.
Вопросы:
1. Сколько рациональных способов раскроя следует использовать?
2. Какое максимальное число комплектов заготовок можно изготовить из имеющегося материала в предположении, что оставшиеся заготовки можно использовать при выполнении следующего заказа?
3. Сколько единиц материала А следует раскраивать третьим способом?
4. Какое максимальное число комплектов заготовок можно изготовить из имеющегося материала, если число заготовок второго типа в комплекте увеличится до семи?
Задача 3. При раскрое деталей для производства единственного изделия на швейной фабрике используются два артикула ткани. Ширина ткани 1 м. Изделие собирается из двух деталей, причем каждая из них может быть получена путем раскроя ткани любого типа. Ткани можно раскраивать тремя способами, количество деталей каждого вида, полученных из одного погонного метра ткани, указано в следующей таблице:

Ткани 1 поступает на фабрику в 2 раза больше (по длине), чем ткани 2. Количество готовых изделий должно быть максимальным.
Вопросы:
1. Сколько способов раскроя ткани 1 следует использовать?
2. Какая часть (в %) ткани 1 должна быть раскроена способом 1?
3. На сколько (в %) изменится выход готовых изделий по сравнению с первоначальным, если на фабрику будет поступать равное количество обеих тканей?
Задача 4. На производство поступила партия стержней длиной 250 и 190 см. Необходимо получить 470 заготовок длиной 120 см и 450 заготовок длиной 80 см. Отходы должны быть минимальны.
Вопросы:
1. Какое количество стержней длиной 250 см надо разрезать?
2. Какое количество стержней длиной 190 см надо разрезать?
3. Какова величина отходов (в см)?
4. Оказалось, что количество стержней длиной 250 см ограничено и равно 200 шт. Какое количество стержней длиной 190 см надо разрезать в этом случае?
5. На сколько при этом увеличатся отходы (в см)?
Задача 5. Завод заключил договор на поставку комплектов стержней длиной 18, 23 и 32 см. Причем количество стержней разной длины в комплекте должно быть в соотношении 1:5:3. На сегодняшний день имеется 80 стержней длиной по 89 см. Как их следует разрезать, чтобы количество комплектов было максимальным?
Вопросы:
1. Сколько существует рациональных способов раскроя?
2. Сколько комплектов стержней будет выпущено?
3. Какова при этом величина отходов (в см)?
Ответы и решения
Ответы на вопросы:1—5, 2 — 4, 3—3, 4—2, 5 — 1.
Задача 1. Решение.
Определим все рациональные способы раскроя прямоугольного листа железа размером 100 х 60 см на квадратные заготовки со сторонами 50, 40 и 20 см.
Получаем шесть рациональных способов раскроя:
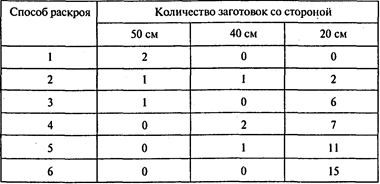
Пусть х1, ..., х6 — количество единиц материала, раскроенных соответствующим способом, х7 — количество изготовленных коробок. Тогда ответ на второй вопрос можно получить, используя следующую модель:
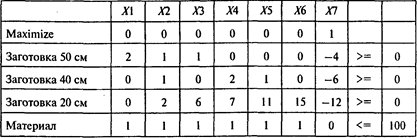
Проводя расчеты, получаем следующий результат:
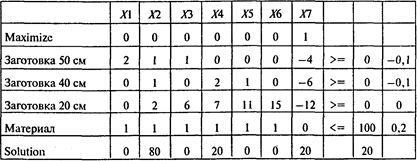
Отсюда следует, что из 100 листов железа можно изготовить 20 ящиков. При этом следует использовать два способа раскроя.
Значение двойственной оценки показывает, что при увеличении количества материала на один лист можно дополнительно изготовить 0,2 коробки.
В следующей таблице приведены границы устойчивости:
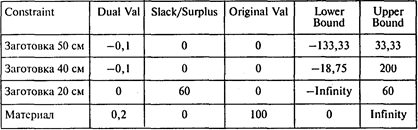
Учитывая границы устойчивости по ограничению «материал», можно сделать вывод, что для изготовления одной коробки требуется пять листов железа.
Ответы: I. Шесть способов. 2. 20 коробок. 3. Два способа. 4. Пять листов.
Задача 2. Решение.
Заметим, что всего существует пять рациональных способов раскроя.
Пусть х1, ..., х5 — количество единиц материала, раскроенных соответствующим способом, х6 — количество комплектов. Тогда используем следующую модель:
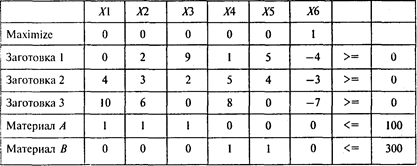
Решая эту задачу, получаем следующий результат:
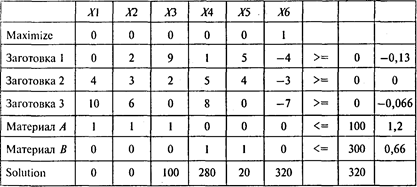
Используется три рациональных способа раскроя из пяти. Из имеющегося материала можно изготовить 320 комплектов заготовок. Третьим способом следует раскраивать все 100 единиц материала А. Для ответа на последний вопрос задачи увеличим количество заготовок в комплекте с 3 до 7. Получим следующий результат:
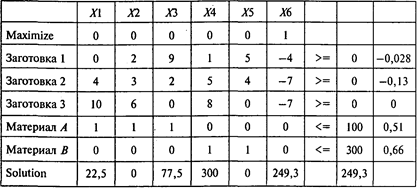
Ответы: 1. Три способа. 2. 320 комплектов. 3. 100 единиц. 4. 249 комплектов.
Задача 3. Решение.
Предположим, что на фабрику поступает 100 м ткани 2. Тогда ткани 1 поступает 200 м. Модель оптимального раскроя будет иметь следующий вид:
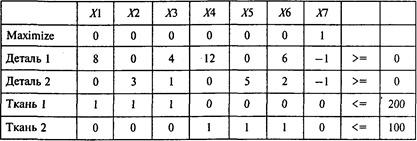
Проводя расчеты, получаем следующий результат:
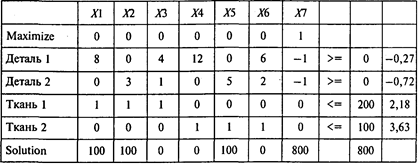
Предположим, что оба вила ткани поступают в равных количествах. Тогда при условии, что общее количество ткани остается неизменным, получаем следующую модель оптимального раскроя:
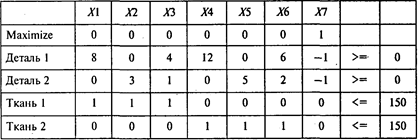
Проводя расчеты, получаем следующий результат:
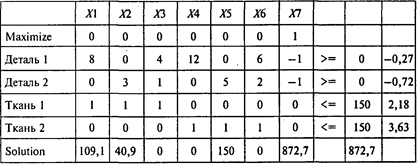
Ответы: 1. Два способа. 2.50%. 3. На 9%.
Задача 4. Решение.
Определяем рациональные способы раскроя материала каждого вида на заготовки. Получаем пять способов, показанных в следующей таблице:
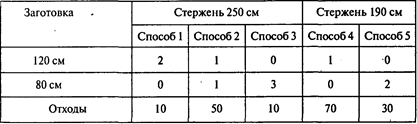
Задача минимизации отходов при условии выполнения задания по изготовлению заготовок описывается следующей моделью:

Проводя расчеты, получаем следующий результат:
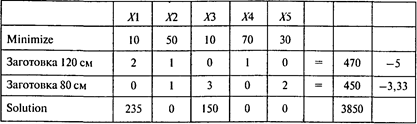
При условии, что количество материала длиной 250 см ограничено, получаем модифицированную модель:
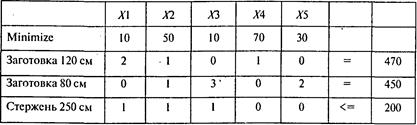
Проводя расчеты, получаем следующий результат:
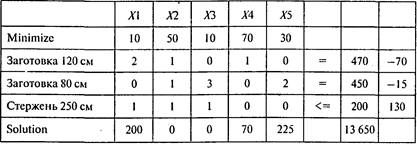
Ответы: 1. 385 стержней. 2. 0. 3. 3850см. 4. 295 стержней. 5. На 9800 см.
Задача 5. Решение.
Определяем рациональные способы раскроя материала каждого вида на заготовки. Получаем девять способов, показанных в следующей таблице:
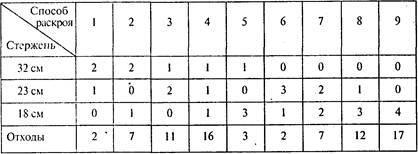
Задача максимизации количества комплектов при ограничении на количество используемого материала описывается следующей моделью:
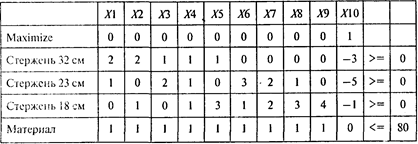
Проводя расчеты, получаем следующий результат:
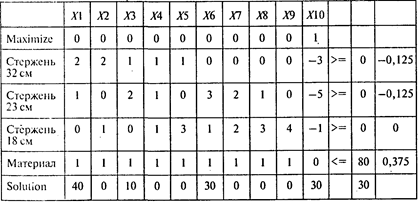
Ответы: 1. Девять способов. 2. 30 комплектов. 3. 250см.
Глава 4. Планирование финансов
Цели
В данной главе показаны возможности использования модели линейного программирования для решения некоторых задач планирования финансов. При определенных предположениях становится возможным выбрать такие способы вложения денег под проценты, совокупность которых позволяет минимизировать первоначальный вклад, необходимый для выплаты займа, или максимизировать доход. При решении задач финансового планирования можно учитывать риск и другие факторы, влияющие на выбор способов вложения денег.
После выполнения заданий, предлагаемых в этой главе, вы будете уметь формулировать и использовать для экономического анализа следующие понятия:
• вклад;
• целевой фонд;
• балансовое ограничение;
• индекс риска по вкладу.
Модели
Модель А минимизации целевого фонда. Предположим, что в определенные моменты времени необходимо выплачивать известные суммы денег по взятому ранее займу. Чтобы накопить эти суммы, можно заранее создать целевой фонд, а средства из этого фонда использовать для срочных вкладов. Каждый срочный вклад характеризуется моментом времени вложения, сроком погашения и доходностью. Задача состоит в том, чтобы определить минимальный размер целевого фонда и выбрать те виды срочных вкладов, которые следует использовать, чтобы сделать выплату по займу. Обозначения:
у — размер целевого фонда, создаваемого в нулевой момент времени;
t — текущий момент времени, t = 0, 1,.... Т;
dt — размер выплаты по займу, которую надо произвести в момент времени t (t = 1, ..., Т);
j —индекс срочного вклада, j = 1,..., п;
vj — момент времени вложения по срочному вкладу j;
wj — срок выплаты по срочному вкладу j;
rj — доходность срочного вклада j (процент по вкладу);
хj — объем вложений по срочному вкладу j.
Предполагается, что для любого срочного вклада j момент vj времени вложения фиксирован. Если по срочному вкладу/сделаны вложения в размере хj, то через wj единиц времени вкладчику выплачивается сумма (1 + rj)хj. Без ограничения общности можно считать, что для любого момента времени существует такой вклад, выплата по которому производится в следующий момент времени. При этом доходность такого вклада может быть нулевая. Использование вклада с нулевой доходностью означает, что деньги остаются на руках у владельца.
Пусть Gt — множество индексов j, таких, что t= vj, т.е. по вкладу j сделано вложение в момент времени t, Qt — множество индексов j, таких, что t = vj + wj, т.е. по вкладу j получена выплата в момент времени t.
Заметим, что для любого t множества Gt и Qt известны.
Тогда модель имеет следующий вид:
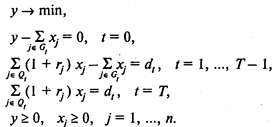
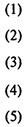
Здесь (1) — целевая функция (минимальный размер целевого фонда);
(2) —условие, характеризующее распределение целевого фонда по вкладам в нулевой момент времени;
(3) — соотношения, устанавливающие баланс между выплатами и вложениями;
(4) — условие, обеспечивающее выплату по займу;
(5) — условия неотрицательности переменных.
Модель В максимизации дохода. Предположим теперь, что вкладчик собирается делать вклады для того, чтобы через определенный период времени получить максимальный доход. Задача состоит в том, чтобы определить величину максимального дохода при фиксированном размере целевого фонда и выбрать те виды срочных вкладов, которые следует использовать.
Сохраним принятые ранее обозначения и введем новые:
z — размер дохода, который может получить вкладчик в момент времени Т;
иt— размер вклада в момент времени t (t = 0, 1,..., Т— 1).
Тогда модель имеет следующий вид:
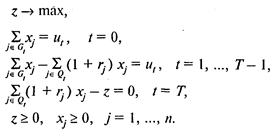
Здесь (6) — целевая функция (максимальная величина дохода);
(7) — условие, характеризующее распределение вклада в нулевой момент времени;
(8) — соотношения, устанавливающие баланс между выплатами и вложениями;
(9) — условие, определяющее величину дохода;
(10)—условия неотрицательности переменных.
Примеры
Пример 1. Вложение денег под проценты.
Петр Перфилов — управляющий компанией, которая только что заключила контракт на покупку нового оборудования для консервирования овощей. В соответствии с договором компания должна выплатить поставщику в общей сложности 750 тыс. руб. Причем 150 тыс. руб. необходимо уплатить через два месяца, а остальные 600 тыс. руб. — через шесть месяцев после того, как оборудование будет поставлено и испытано. Петр считает, что сразу после подписания договора следует образовать целевой фонд и использовать эти средства для вложения денег под проценты. Поскольку такие инвестиции породят дополнительную наличность к тому времени, когда придется вносить деньги за оборудование, Петр понимает, что целевой фонд должен быть меньше чем 750 тыс. руб. А вот сколько именно — зависит от имеющихся возможностей инвестирования.
Проанализировав варианты, Петр решил сосредоточиться на 12 возможных способах вложения денег под проценты. Виды вкладов, их продолжительность, возможные сроки вложения и проценты по вкладу приведены в следующей таблице:

Данные о возможностях вложений и возврата денег (в руб.) представлены в следующей таблице:

С учетом этих возможностей необходимо минимизировать размер целевого фонда, обеспечивающего оплату оборудования.
Вопросы:
1. Каков минимальный размер целевого фонда, позволяющий сделать необходимые выплаты?
2. Какова стоимость в начальный момент времени одного рубля, который надо выплатить в начале седьмого месяца (через шесть месяцев)?
3. Какова стоимость в начальный момент времени одного рубля, который надо выплатить в начале пятого месяца (через четыре месяца)?
Решение. Введем следующие обозначения:
у — размер целевого фонда;
Аi — размер вклада вида А в месяце i;
Bi — размер вклада вида В в месяце i;
Сi — размер вклада вида С в месяце i;
Di — размер вклада вида D в месяце i.
Так как в любой момент времени можно сделать вклад на один месяц, хранить деньги на руках невыгодно. С учетом этого условия задача минимизации целевого фонда может быть описана следующей моделью:
Целевая функция
у ® min
при условиях
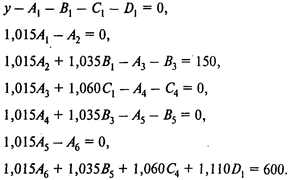
Эту модель можно представить в следующей, более наглядной форме:
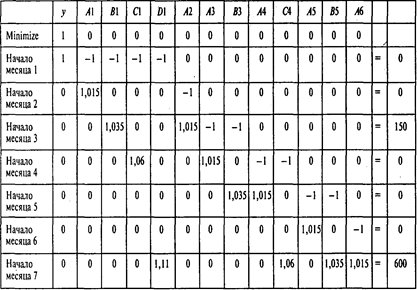
Проводя вычисления, получаем следующие результаты:
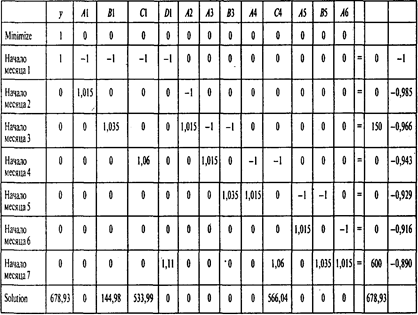
Следующая таблица содержит границы устойчивости по коэффициентам целевой функции:
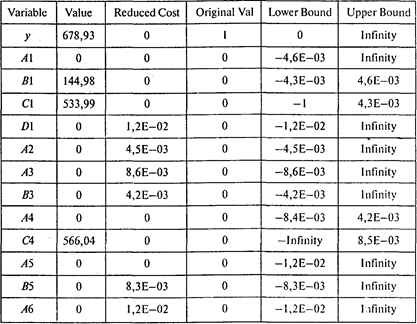
Далее приводятся границы устойчивости по правым частям ограничений:
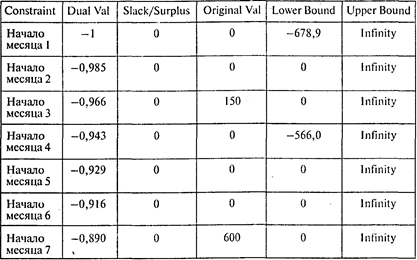
В этой модели особый интерес представляет интерпретация двойственных оценок. Например, двойственная оценка последнего ограничения равна —0,89. Это означает, что для выплаты через полгода одного дополнительного рубля необходимо увеличить размер целевого фонда на 0,89 руб. Таким образом, величина двойственной оценки есть стоимость одного рубля, выплачиваемого через полгода, приведенная к начальному моменту времени.
Ответы: 1.678,93 тыс. руб. 2.0,89руб. 3.0,929руб.
Вопросы
Вопрос 1. Срочный вклад характеризуется:
1) суммой вклада и процентом по вкладу;
2) моментом вложения, сроком погашения, прибылью и процентом по вкладу;
3) размером вклада, моментом вложения, сроком погашения и процентом по вкладу;
4) размером вклада, моментом вложения, сроком погашения, прибылью и процентом по вкладу.
Вопрос 2. Целью модели минимизации целевого фонда является:
1) минимизация целевого фонда, необходимого для накопления определенной суммы;
2) максимизация целевого фонда, необходимого для накопления определенной суммы;
3) минимизация размера срочного вклада, необходимого для накопления определенной суммы;
4) максимизация размера срочного вклада, необходимого для накопления определенной суммы;
5) минимизация целевого фонда, необходимого для получения максимального дохода.
Вопрос 3. Целью модели максимизации дохода является:
1) максимизация целевого фонда, необходимого для получения максимального дохода;
2) минимизация целевого фонда, необходимого для получения максимального дохода;
3) выбор срочного вклада с максимальной доходностью;
4) минимизация дохода при фиксированной величине целевого фонда;
5) максимизация дохода при фиксированной величине целевого фонда.
Задачи
Задача 1. Константин Иванов — управляющий компанией «Золотой колос», специализирующейся на выпуске пива. Компания закупила оборудование для выпуска популярного сорта пива «Двойное золотое». Стоимость оборудования 900 тыс. руб. В соответствии с условиями контракта 200 тыс. руб. необходимо выплатить через два месяца, когда оборудование будет поставлено, а оставшиеся 700 тыс. руб. — через шесть месяцев, когда оборудование будет смонтировано.
Чтобы расплатиться полностью, Константин предполагает тотчас же образовать целевой фонд, который можно использовать для инвестиций. Поскольку такие инвестиции породят дополнительную наличность к тому времени, когда придется вносить деньги за оборудование, Константин знает, что ему следует отложить меньше чем 900 тыс. руб. А вот сколько именно — зависит от имеющихся возможностей инвестирования.
Константин решил сосредоточиться на 12 возможностях инвестирования.
Данные для задачи финансового планирования представлены в следующей таблице:

Для каждого вида вкладов известна экспертная оценка риска задержки выплаты по вкладу.
Составьте модель линейного программирования для определения минимального размера целевого фонда, позволяющего сделать необходимые выплаты.
Вопросы:
1. Каков минимальный размер целевого фонда, позволяющий сделать необходимые выплаты без учета риска?
2. Какова стоимость в начальный момент времени одного рубля, который надо выплатить в начале седьмого месяца (через шесть месяцев)?
3. Каков минимальный размер целевого фонда, позволяющий сделать необходимые выплаты, если средний риск в каждый момент времени не должен превышать 6?
4. Какова «плата» за снижение риска (в руб.)?
Задача 2. У Василия Иванова есть 50 тыс. руб., которые можно инвестировать. Необходимо максимизировать денежную наличность к концу шестимесячного периода. Возможные виды инвестиций представлены в следующей таблице:

Для каждого вида вкладов известна экспертная оценка риска задержки выплаты по вкладу.
Составьте модель линейного программирования для определения максимального размера дохода, который может получить Василий Иванов через полгода, использовав имеющиеся у него возможности для вложения 50 тыс. руб.
Вопросы:
1. Каков максимальный размер дохода через полгода?
2. Какой максимальный доход можно получить через полгода от вложения одного рубля в начальный момент времени?
3. Какой максимальный размер дохода можно получить через полгода, если средний риск в каждый момент времени не должен превышать б?
4. Какова «плата» за снижение риска (в руб.)?
5. В начале четвертого месяца Василий предполагает вложить еще 20 тыс. руб. На сколько возрастет его доход через полгода с учетом риска?
Задача 3. Пять проектов конкурируют за получение инвестиционных фондов компании.
Проект 1 предполагает вложение денег в 2003 г., получение 30% по вкладу в 2004 г. и возврат вложенных средств (без процентов)
в 2005 г.
Проект 2 предполагает вложение денег в 2004 г., получение 30% по вкладу в 2005 г. и возврат вложенных средств (без процентов) в 2006 г.
Проект 3 предполагает вложение денег в 2003 г. и получение 1,75 руб. на один вложенный рубль в 2006 г.
Проект 4 предполагает вложение денег в 2005 г. и получение 1,4 руб. на один вложенный рубль в 2006 г.
Проект 5 предполагает вложение денег в 2003 г. и получение 1,2 руб. на один вложенный рубль в 2005 г.
Максимальная сумма, которая может быть вложена в любой проект, не должна превышать 10 млн руб.
Деньги, полученные в результате инвестиций в один проект, можно реинвестировать в другие проекты.
Компания также может получать 6% годовых по краткосрочному (на один год) банковскому вкладу.
К началу 2003 г. инвестиционный фонд компании составит 20 млн руб. Целью компании является максимизация дохода от инвестиций к 2006 г.
Вопросы:
1. Какова максимальная сумма денег, которую можно получить в 2006 г.?
2. Какую сумму следует вложить во второй проект?
3. В каком году следует вложить деньги в банк под 6% годовых?
4. Какой максимальный доход можно получить в 2006 г., вложив 1 руб. в 2003 г.?
Ответы и решения
Ответы на вопросы: 1—4, 2 — 1, 3—5.
Задача 1. Решение.
Пусть у — размер целевого фонда. Аi, Bi, Сi, Di — размеры вкладов вида А, В, С, D в i-м месяце. Так как в любой момент времени можно сделать вклад на один месяц, хранить деньги на руках невыгодно. С учетом этого условия задача может быть описана следующей моделью:
Целевая функция
у ® min
при условиях
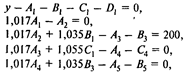
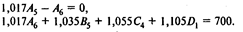
Представим модель в более наглядной форме:
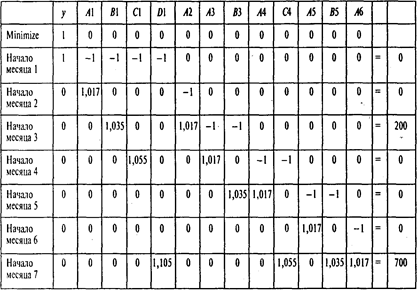
Решая эту задачу, получаем следующие результаты:
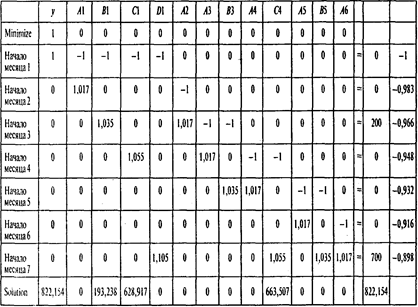
Следующая таблица содержит границы устойчивости по коэффициентам целевой функции:
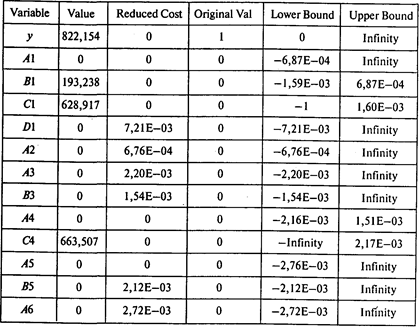
Далее приводятся границы устойчивости по правым частям ограничении:
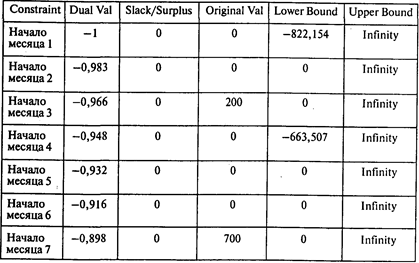
Ограничение, учитывающее риск по вкладам, сделанным в месяце 1, может быть записано следующим образом:
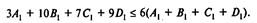
После преобразования система ограничений, учитывающих риск, имеет следующий вид:
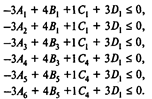
С учетом риска получаем модель с 13 переменными и 13 ограничениями:
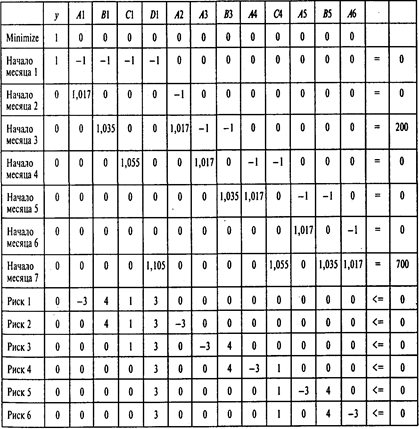
Решая эту задачу, получаем следующие результаты:
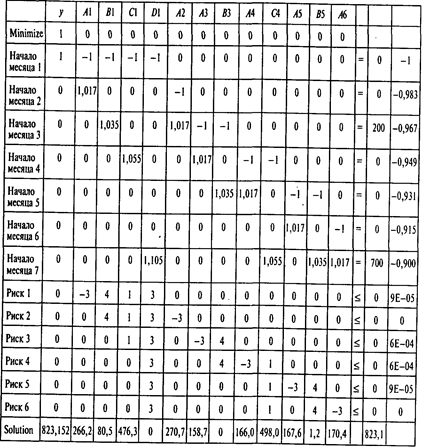
Границы устойчивости по коэффициентам целевой функции:
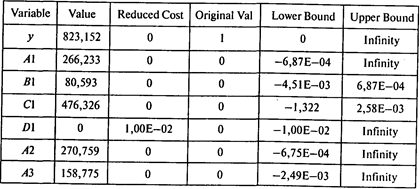
Окончание таблицы
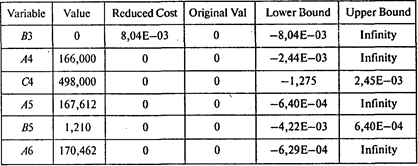
Границы устойчивости по правым частям ограничений:
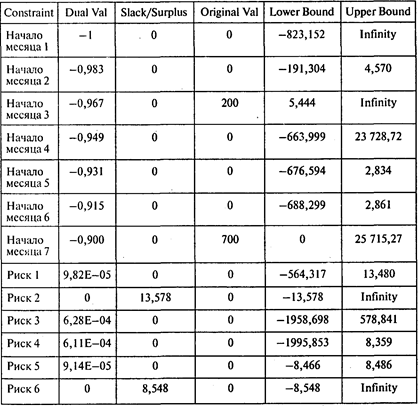
Ответы: 1. 822154 руб. 2. 0,9 руб. 3. 823152 руб. 4. 998 руб.
Задача 2.
Решение.
Пусть z — размер дохода, Аi, Вi, Сi, Di — размеры вкладов соответствующего вида в i-м месяце. Так как в любой момент времени можно сделать вклад на один месяц, хранить деньги на руках невыгодно. Без учета риска задача может быть описана следующей моделью:
Целевая функция
z ® max
при условиях
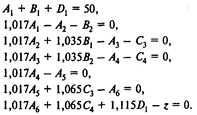
Представим модель в более наглядной форме:
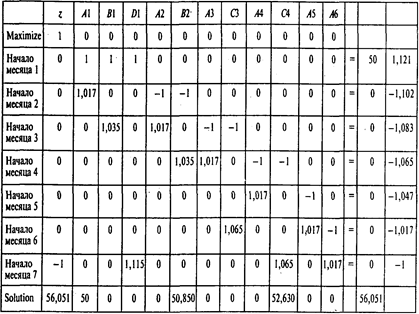
Границы устойчивости по коэффициентам целевой функции:
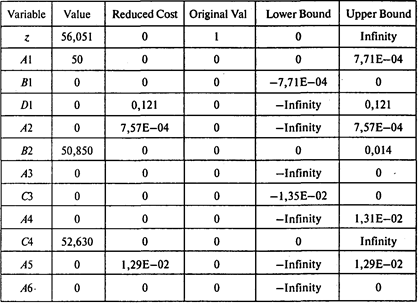
Границы устойчивости по правым частям ограничений:
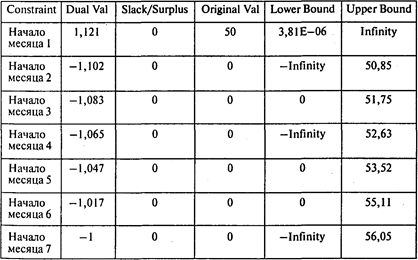
Система ограничений, учитывающих риск, имеет следующий вид:
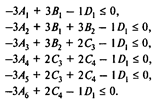
С учетом риска получаем задачу с 12 переменными и 13 ограничениями. Проводя расчеты, получаем следующие результаты:
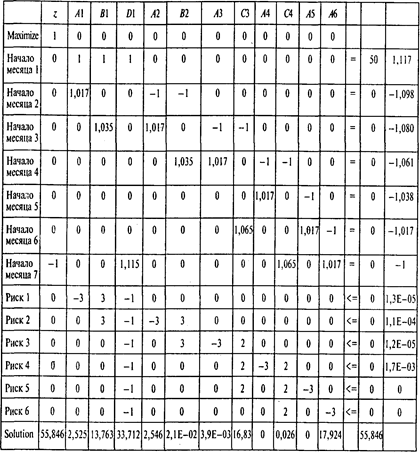
С учетом возможности вложения дополнительных 20 тыс. руб. четвертое ограничение будет иметь вид
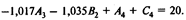
Решая модифицированную задачу, получаем следующий результат:
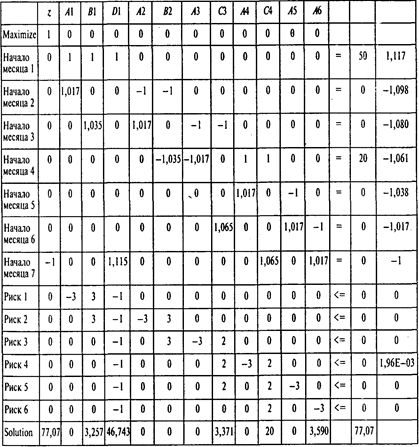
Ответы: 1. 56051 руб. 2. 1,12 руб. 3. 55846 руб. 4. 205руб. 5. 21019 руб.
Задача 3.
Решение.
Пусть х1, ...,x5— размер вклада в соответствующий проект, x6, х7, x8 — размер вклада в банк, а x9 — размер дохода.
Задача описывается с помощью модели линейного программирования:
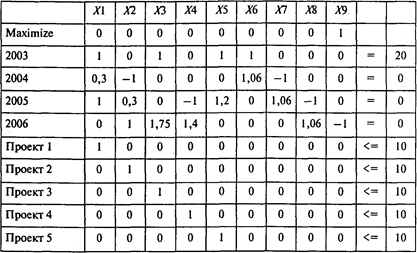
Проводя расчеты, получаем следующий результат:
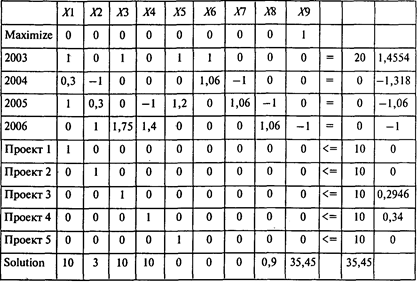
Ответы: 1. 35,45 млн руб. 2. 3 млн руб. 3. В 2005 г. 4. 1,45 руб.
Глава 5. Транспортная задача
Цели
В данной главе рассматривается задача транспортировки продукта, который в определенных количествах предлагается различными производителями. Известны потребности нескольких потребителей в этом продукте. Требуется определить, от каких производителей и в каких объемах должны получать продукт потребители. Поставки должны осуществляться таким образом, чтобы совокупные издержки на транспортировку продукта были минимальными.
После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь составлять и использовать для экономического анализа:
• замкнутую и открытую транспортные задачи;
• транспортную задачу с запретами;
• транспортную задачу с фиксированными перевозками;
• транспортную задачу с ограничениями на пропускную способность;
• транспортную задачу с фиксированными доплатами;
• транспортную таблицу.
Модели
Обозначения:
аi — величина предложения продукта в пункте i (i = 1, ..., n);
bj — величина спроса на продукт в пункте j (j = 1,..., т);
cij — затраты на транспортировку единицы продукта из пункта i в пункт j;
xij — количество продукта, перевозимого из пункта i в пункт j.
Модель транспортной задачи:
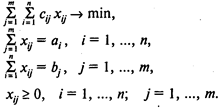
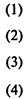
Здесь (1) — целевая функция (минимум затрат на транспортировку продукта);
(2) — ограничения по величине предложения в каждом пункте производства;
(3) — ограничения по величине спроса в каждом пункте потребления;
(4) — условия неотрицательности объемов перевозок.
1. Замкнутая транспортная задача. Общее предложение равно общему спросу:
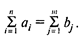
Это необходимое и достаточное условие существования допустимого плана задачи (1)—(4).
Дата добавления: 2016-07-09; просмотров: 5601;
