Минимизация затрат, необходимых для сокращения времени реализации проекта.

Обозначения:

(i, j) — работа проекта в соответствии с опре­делениями, данными в главе 7;

t_ij — нормальная продолжительность рабо­ты (i,j) (продолжительность работы при детерминированном подходе — ме­тод СРМ или ожидаемое время выпол­нения работы при стохастическом под­ходе — метод PERT);

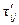— продолжительность работы (i,j) при максимально возможном ее сокраще­нии;

М_ij = t_ij – 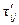— величина максимально возможного со­кращения продолжительности работы (i,j) за счет дополнительных ресурсов;

С_ij — расчетные затраты на выполнение рабо­ты (i,j) при нормальной ее продолжи­тельности;

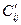— расчетные затраты на выполнение рабо­ты (i,j) в условиях максимального со­кращения ее продолжительности за счет дополнительных ресурсов;

К_ij = ( 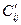– С_ij)/М_ij — удельные затраты на сокращение про­должительности работы (i,j) (на едини­цу времени).

Предположим, что любая дополнительная доля сокращаемого времени на выполнение работы потребует постоянной (неизмен­ной во времени) доли дополнительных затрат. При таком пред­положении для минимизации затрат на сокращение времени реа­лизации проекта можно использовать модель линейного программи­рования.

Для формулировки модели дополнительно введем следующие обозначения:

Р — множество работ проекта;

х_i — время наступления события i (событие-узел отражает факт завершения всех работ, входящих в данный узел);

у_ij — величина сокращения времени работы (i, j);

i = 1 —номер начального события для сети, описывающей проект;

i = п —номер конечного события для сети, описывающей проект;

T₀ — желательное время выполнения проекта.

При данных обозначениях модель линейного программирова­ния имеет вид

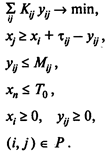
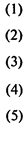
Если т — число работ, п — число событий, то описанная мо­дель имеет п + т переменных, т ограничений (2), т ограниче­ний (3), п + т ограничений (5) и одно ограничение (4). Итого п + т переменных и 3т + n + 1 ограничение.

Если {x_j*, у_ij*} — оптимальный план, полученный для модели (1)—(5), то у_ij* — время, на которое следует сократить продолжи­тельность выполнения работы (i,j); 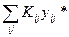— минимальная сум­ма издержек, необходимая для сокращения времени выполнения проекта до T₀.

2. Метод анализа затрат PERT/COST. Метод основан на по­строении области допустимых затрат, при которых проект может быть реализован за определенное время. В результате применения метода СРМ или метода PERT может быть получено наиболее раннее и наиболее позднее время начала каждой работы. Далее строятся два графика: график совокупных затрат при наиболее раннем времени начала работ и график совокупных затрат при наиболее позднем времени начала работ.

Если фактические затраты на выполнение проекта будут нахо­диться внутри области, очерченной этими графиками, то проект может быть выполнен за время, соответствующее длине критичес­кого пути. Если фактические затраты окажутся за пределами очерченной области, то продолжительность выполнения проекта увеличится.

Примеры

Пример 1. Минимизация затрат на сокращение времени реали­зации проекта.

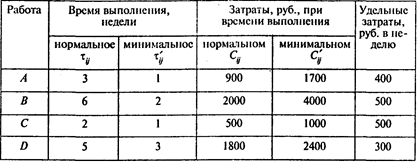
Проект пусконаладки компьютерной системы состоит из вось­ми работ. В следующей таблице указаны взаимосвязь работ, нор­мальное время их выполнения и данные, характеризующие воз­можность сокращения продолжительности работ:

Определите минимальную продолжительность проекта при нормальном времени выполнения работ. Можно ли уменьшить продолжительность проекта при дополнительных затратах?

Вопросы:

1. Какова продолжительность проекта при нормальном време­ни выполнения работ?

2. Сколько работ в этом случае являются критическими?

3. Каковы затраты на выполнение проекта при нормальном времени выполнения работ?

4. С какими минимальными дополнительными затратами мож­но выполнить этот проект за 16 недель?

Решение. Найдем критический путь при нормальном време­ни выполнения работ. Используем для этого метод СРМ. Вводим в программу POMWIN исходную информацию, описывающую проект в виде последовательности работ:

Выполнив расчеты, получаем следующие результаты:

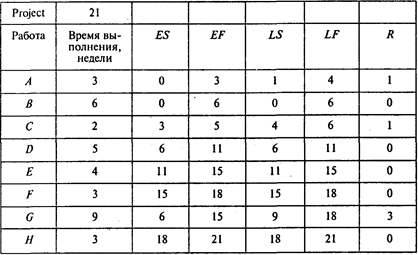
Отсюда видно, что при нормальной продолжительности работ длина критического пути составляет 21 неделю. На критическом пути находятся работы В, D, Е, F, Н. Для того чтобы определить затраты на выполнение проекта при нормальной продолжитель­ности работ, достаточно просуммировать затраты, указанные в пятом столбце таблицы исходных данных. В результате получаем затраты 18 700 руб.

Для определения минимальных дополнительных издержек, необходимых для того, чтобы снизить продолжительность проек­та до 16 недель, построим модель линейного программирования. Для этого на основании данных о непосредственно предшеству­ющих работах построим графическое представление проекта (рис. 1).

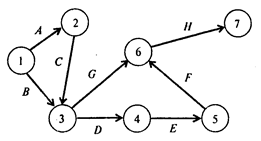
Рис. 1

Используя исходные данные, определяем удельные (в едини­цу времени) затраты К_ij на сокращение продолжительности работ. Получаем следующие результаты:

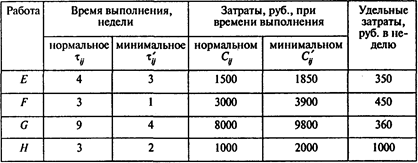
Окончание таблицы

Используя обозначения х_i — время наступления события i, у_ij — величина сокращения времени работы (i,j), получаем сле­дующую модель линейного программирования для определения минимальных издержек, необходимых для сокращения продолжи­тельности проекта с 21 до 16 недель:

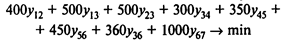
при условиях

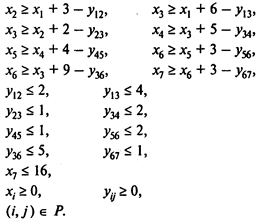
Для решения этой задачи линейного программирования ис­пользуем программу POMWIN.

В следующей таблице приведенная выше модель представлена в формате программы POMWIN:

Выполнив расчеты, получаем следующие результаты:

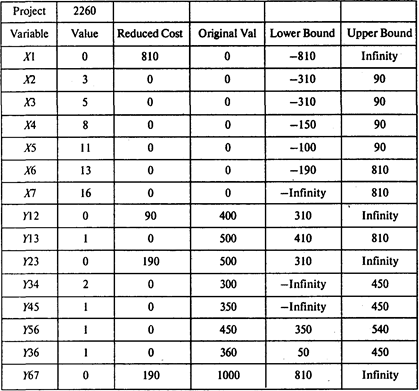
Итак, минимальные затраты, необходимые для того, чтобы со­кратить продолжительность проекта с 21 до 16 недель, составля­ют 2260 руб.

Продолжительность каждой из работ (1, 3), (4, 5), (5, 6) и (3, 6) сокращается на одну неделю. Продолжительность работы (3, 4) сокращается на две недели.

Ответы: 1. 21 неделя. 2. Пять работ. 3. 18 700 руб. 4. 2260 руб.

Пример 2. Контроль затрат на выполнение проекта.

Перечень работ проекта, время их выполнения и оценки за­трат на выполнение работ отражены в следующей таблице:

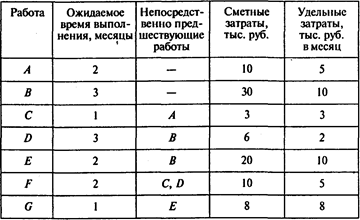
Удельные затраты определены в предположении о том, что за­траты производятся равномерно в течение срока выполнения работы.

Определите, в каком диапазоне могут меняться фактические затраты на выполнение проекта при условии, что проект будет выполнен за минимальное время.

Вопросы:

1. За какое минимальное время может быть выполнен проект?

2. При каком максимальном значении совокупных затрат, сде­ланных за первые 3 месяца реализации проекта, проект мо­жет быть выполнен за минимальное время?

3. При каком минимальном значении совокупных затрат, сде­ланных за первые 3 месяца реализации проекта, проект мо­жет быть выполнен за минимальное время?

4. При каком максимальном значении совокупных затрат, сде­ланных за 6 месяцев реализации проекта, проект может быть выполнен за минимальное время?

5. При каком минимальном значении совокупных затрат, сде­ланных за 6 месяцев реализации проекта, проект может быть выполнен за минимальное время?

Решение. Определим минимальное время выполнения проек­та. Найдем критический путь, воспользовавшись методом СРМ. Введем в программу POMWIN информацию о предшествующих работах и времени их выполнения:

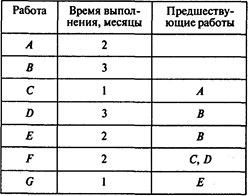
Результаты расчетов представлены в следующей таблице:

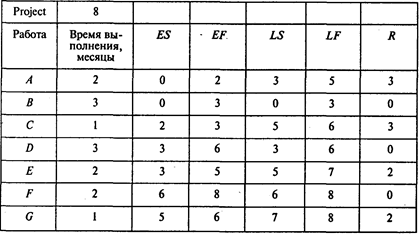
Ожидаемое время выполнения проекта равно 8 месяцам.

Определим динамику совокупных затрат для графика выпол­нения проекта с наиболее ранним началом всех работ:

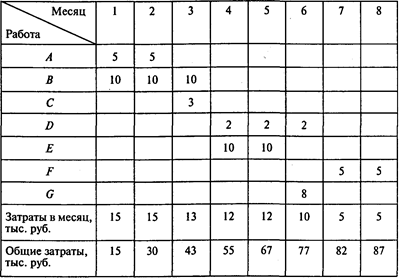
Определим динамику совокупных затрат для графика выпол­нения проекта с наиболее поздним началом всех работ:

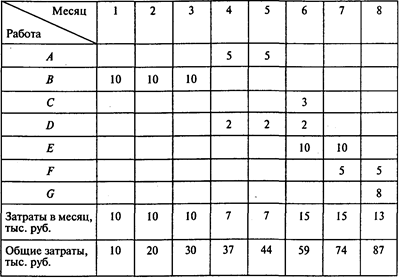
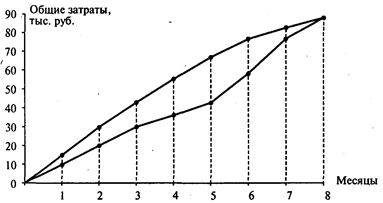
Рис. 2

На рис. 2 показаны два графика. Выше проходит график совокуп­ных затрат при наиболее раннем времени начала работ, ниже — при наиболее позднем времени начала работ. Если фактические за­траты на выполнение проекта будут находиться внутри очерчен­ной области, то проект может быть выполнен за 8 месяцев. Если фактические затраты окажутся за пределами очерченной области, то продолжительность проекта увеличится.

Таким образом, менеджер может контролировать фактические затраты по проекту. Если сметные затраты не выполнены или до­пущен перерасход, необходимо осуществлять корректирующие воздействия, сдвигая время начала отдельных работ и (или) сокра­щая их продолжительность путем привлечения дополнительных ресурсов.

Ответы: 1. Восемь месяцев. 2. 43 тыс. руб. 3. 30 тыс. руб. 4. 77 тыс. руб. 5. 59 тыс. руб.

Вопросы

Вопрос 1. Для определения минимальных затрат, необходимых для выполнения проекта за фиксированное время, следует исполь­зовать:

1) метод СРМ;

2) метод PERT;

3) модель линейного программирования;

4) модель транспортного типа;

5) все вышеперечисленное.

Вопрос 2. Пусть в графе, описывающем проект, т работ и п событий (вершин сети). Число переменных в модели линейно­го программирования для определения минимальных затрат, не­обходимых для выполнения проекта за фиксированное время, равно:

1) т;

2) п;

3) т+ п;

4) т– п;

5) т • п.

Вопрос 3. Какую формулу следует использовать для определе­ния величины удельных затрат К_ij на сокращение продолжитель­ности работы (i, j)?

Варианты ответов:

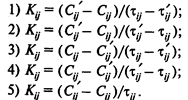
Вопрос 4. Какое из указанных далее соотношений является верным?

Варианты ответов:

1) совокупные затраты при наиболее позднем времени начала работ превышают совокупные затраты при наиболее раннем вре­мени начала работ;

2) совокупные затраты при наиболее раннем времени начала работ превышают совокупные затраты при наиболее позднем вре­мени начала работ;

3) совокупные затраты при наиболее раннем времени начала работ равны совокупным затратам при наиболее позднем време­ни начала работ;

4) совокупные затраты при наиболее раннем времени начала работ превышают совокупные затраты при наиболее позднем вре­мени начала работ на величину сметной стоимости проекта;

5) совокупные затраты при наиболее раннем времени начала работ и совокупные затраты при наиболее позднем времени на­чала работ постоянны.

Вопрос 5. Для осуществления контроля за расходованием средств на выполнение проекта используется:

1) метод СРМ;

2) метод PERT;

3) модель линейного программирования;

4) все вышеперечисленное;

5) метод PERT/COST.

Задачи

Задача 1. Рассмотрите следующую сеть проекта с показателя­ми продолжительности работ (в неделях) и информацией о затра­тах на сокращение продолжительности работ (в тыс. руб.) за счет привлечения дополнительных финансовых средств:

Найдите критический путь и затраты на реализацию проекта при нормальном времени выполнения всех работ.

Предположим, что руководство хотело бы завершить проект в 10-недельный срок. Постройте модель линейного программи­рования, которую можно было бы использовать для того, чтобы определить минимальные затраты на сокращение времени выпол­нения проекта.

Вопросы:

1. Какова продолжительность проекта при нормальном време­ни выполнения работ?

2. Каковы затраты на выполнение проекта при нормальной продолжительности работ?

3. Чему равны минимальные затраты на выполнение проекта в 10-недельный срок?

4. Для какого количества работ необходимо сократить время выполнения, чтобы завершить проект за 10 недель?

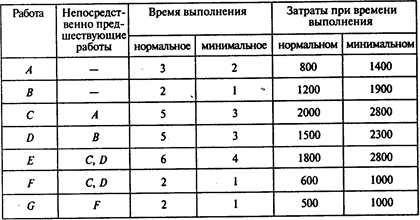
Задача 2.В следующей таблице представлена информация о продолжительности работ проекта (в месяцах) и затратах на их выполнение (в тыс. руб.):

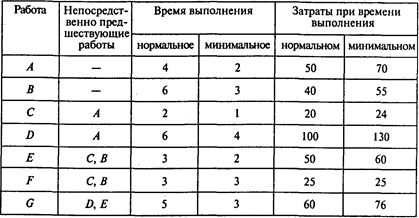
Найдите критический путь и продолжительность проекта при нормальном времени выполнения работ.

Вопросы:

1. Какова продолжительность проекта при нормальном време­ни выполнения работ?

2. Каковы затраты на выполнение проекта при нормальной продолжительности работ?

3. Чему равны минимальные затраты на выполнение проекта за один год?

4. За какое минимальное время может быть выполнен проект?

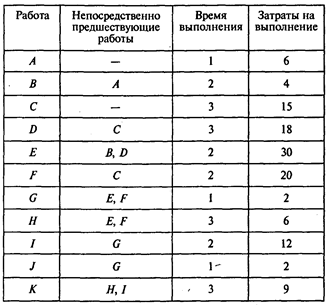
Задача 3. Отдел ЭВМ экономического факультета МГУ разра­ботал предложения по внедрению новой компьютерной системы для нужд администрации факультета. В предложения включен перечень работ, которые необходимо выполнить, чтобы ввести систему в действие. Соответствующая информация представлена в следующей таблице (время — в неделях, затраты — в тыс. руб.):

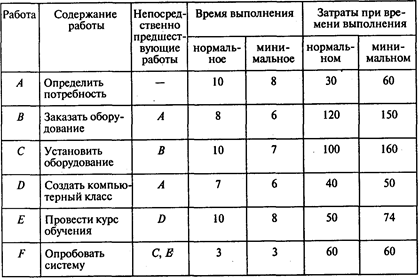
Вопросы:

1. Какова продолжительность проекта при нормальном време­ни выполнения работ?

2. Каковы затраты на выполнение проекта при нормальной продолжительности работ?

3. Чему равны минимальные затраты на выполнение проекта за 26 недель?

4. За какое минимальное время может быть выполнен проект?

Задача 4. Конструкторское бюро Московского часового завода (МЧЗ) разработало новый настольный радиобудильник. По мне­нию проектировщиков, запуск в серию нового продукта позволит расширить рынок сбыта и получить дополнительную прибыль.

Руководство МЧЗ решило изучить возможности реализации нового продукта. Результатом исследования должны стать реко­мендации относительно действий, которые следует предпринять для организации производства и сбыта нового продукта.

Перечень работ, время, необходимое для их выполнения (в не­делях), и затраты (в тыс. руб.) указаны в следующей таблице:

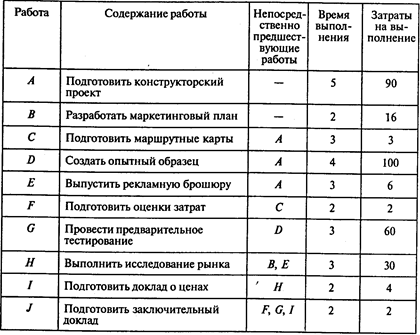
Определите критический путь для данного проекта, наиболее раннее и наиболее позднее время начала каждой работы. Опреде­лите динамику роста общих затрат на проект, основанную на дан­ных о наиболее раннем и наиболее позднем времени начала работ.

Используйте полученные оценки сметных расходов для конт­роля за фактическим расходованием средств. Предполагается, что все работы финансируются пропорционально времени их выпол­нения.

Вопросы:

1. За какое минимальное время может быть выполнен проект?

2. Чему равно максимальное значение совокупных затрат на ко­нец пятой недели, при котором проект может быть выполнен за время, соответствующее длине критического пути?

3. Чему равно минимальное значение совокупных затрат на ко­нец пятой недели, при котором проект может быть выпол­нен за время, соответствующее длине критического пути?

4. Какова величина недостатка или перерасхода средств в кон­це пятой недели, если фактические затраты в этот момент составили 100 тыс. руб.?

5. Какова величина недостатка средств в конце десятой не­дели, если фактические затраты в этот момент составили 230 тыс. руб.?

Задача 5. Ниже представлена сеть проекта, а также данные о времени выполнения работ (в неделях) и затратах (в тыс. руб.):

Определите критический путь для данного проекта, наиболее раннее и наиболее позднее время начала каждой работы. Опреде­лите динамику роста общих затрат на проект, основанную на дан­ных о наиболее раннем и наиболее позднем времени начала работ.

Используйте полученные оценки сметных расходов для конт­роля за фактическим расходованием средств. Предполагается, что все работы финансируются пропорционально времени их выпол­нения.

Вопросы:

1. За какое минимальное время может быть выполнен проект?

2. Чему равно максимальное значение совокупных затрат на ко­нец четвертой недели, при котором проект может быть вы­полнен за время, соответствующее длине критического пути?

3. Чему равно минимальное значение совокупных затрат на ко­нец четвертой недели, при котором проект может быть вы­полнен за время, соответствующее длине критического пути?

4. Какова величина недостатка или перерасхода средств в кон­це четвертой недели, если фактические затраты в этот мо­мент составили 35 тыс. руб.?

5. Какова величина недостатка средств в конце восьмой недели, если фактические затраты в этот момент составили 90 тыс. руб.?

Ситуации

Ситуация 1. Компания «Космо».

В рамках подготовки старта космического корабля по програм­ме совместных исследований с Национальным бюро аэронавти­ки (НБА) США российская компания «Космо» готовит к подпи­санию проект модернизации ракетного стартового комплекса на космодроме Байконур. Этот контракт предусматривает строитель­ство центрального здания телеуправления (ЦЗТ). Финансирует проект американская сторона.

Первоначальный граф проекта строительства ЦЗТ приведен на рис. 3 (на схеме работы, лежащие на критическом пути, отмече­ны полужирной стрелкой).

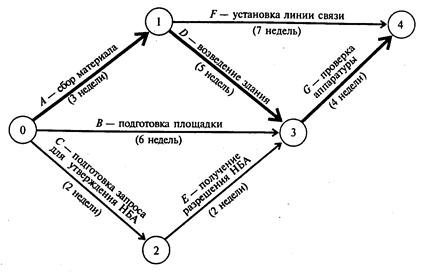
Рис.3

Руководитель проекта менеджер компании «Космо» Владимир Алексеев определил время выполнения и сметные затраты для каждой работы проекта:

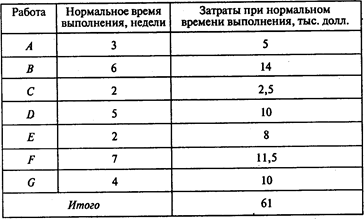
Оказалось, что критический путь для данного проекта состав­ляют работы A, D и G. При нормальном времени выполнения всех работ проект может быть реализован за 12 недель. Сметная сто­имость проекта в этом случае составляет 61 тыс. долл.

Заказчика работ предлагаемый компанией «Космо» срок не устраивает. Все работы необходимо завершить за 9 недель. При этом бюджет проекта не должен превысить 80 тыс. долл. Проведя дополнительные расчеты, Владимир Алексеев оценил минимальное время на выполнение каждой работы (в неделях) и затраты при минимальном времени выполнения (в тыс. долл.):

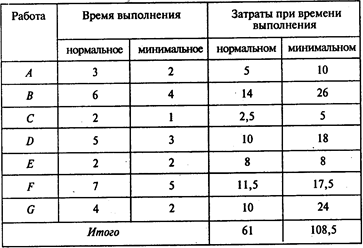
Используйте метод PERT/COST для анализа продолжительно­сти проекта и затрат на его реализацию.

Задания

1. Определите, можно ли выполнить проект за 9 недель. Если да, то с какими минимальными затратами? Сколько крити­ческих путей будет в этом случае и какие работы будут кри­тическими?

2. Определите, можно ли выполнить проект за 7 недель. Если да, то с какими минимальными затратами?

Ситуация 2. Строительная компания Хоупа.

Строительная компания Хоупа активно занимается подготов­кой нового проекта строительства фабрики для корпорации SBPA. Пару лет назад президенту корпорации SBPA Эрику Кляйну по­нравился предварительный план проектирования и строительства фабрики, подготовленный Хоупом, и он решил отдать предпоч­тение его строительной компании.

Хоуп поручил начальнику проектного отдела Деврону Вильямсу провести сетевой анализ работ в рамках проекта с учетом пред­полагаемых издержек. Вильяме дал указание своим сотрудникам разделить проект строительства фабрики на отдельные работы и установить их взаимосвязь. Для каждой работы следовало опре­делить нормальное время ее выполнения и соответствующие за­траты. Требовалось также оценить минимальное время выполне­ния работы и соответствующие этому времени затраты.

Результаты, представленные сотрудниками отдела, приведены в таблице (время выполнения работ указано в неделях, затраты — в тыс. долл.):

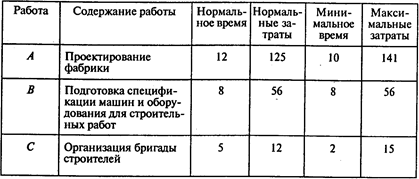
Окончание таблицы

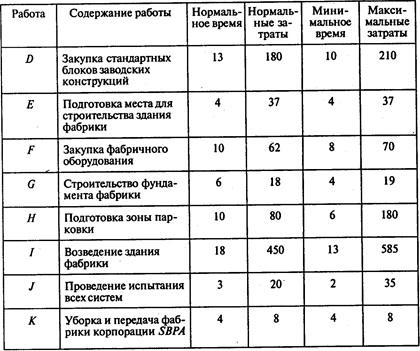
Результаты анализа взаимосвязи работ представлены Вильямсу в следующем докладе:

1. Начальная работа А — спроектировать фабрику.

2. После выполнения проектных изысканий следуют работы В — ­подготовить спецификацию машин и оборудования для строитель­ных работ, С — организовать бригаду строителей и D — закупить стандартные блоки заводских конструкций.

3. После завершения работ В и С строительной бригаде необ­ходимо выполнить работу Е — подготовить место для строитель­ства здания фабрики. В то же время, пока ведется подготовка ме­ста для строительства, можно приступить к работам F— закупке фабричного оборудования и G — строительству фундамента фаб­рики.

4. После подготовки места для строительства необходимо вы­полнить работу H — подготовить зону парковки.

5. Работу I — возведение здания фабрики — можно выполнить после того, как будут закуплены стандартные блоки заводских конструкций, подготовлено место для строительства, закуплено фабричное оборудование и построен фундамент фабрики.

6. После завершения строительства здания фабрики и подго­товки зоны парковки компания Хоупа может приступить к рабо­те J — проведению испытания всех систем. Затем проводится убор­ка (работа К) и фабрика передается корпорации SBPA.

Корпорация SBPA крайне заинтересована в том, чтобы строи­тельство фабрики было завершено как можно быстрее. По пред­ложению Эрика Кляйна в контракт включен пункт, предусматри­вающий премию в 25 тыс. долл. за каждую неделю сокращения срока выполнения проекта по сравнению с годом. В то же время контрактом предусмотрен штраф в 25 тыс. долл. за каждую неде­лю превышения срока выполнения проекта по сравнению с годом.

После подписания контракта Хоуп озабочен тем, чтобы завер­шить проект как можно раньше. По его указанию расчетный от­дел провел калькуляцию накладных расходов. Первый тип наклад­ных расходов — обычные накладные расходы в размере 22,5% от прямых затрат на выполнение работ. Накладные расходы второго типа зависят от продолжительности проекта в целом. Эти наклад­ные расходы увеличиваются на 1500 долл. каждую неделю. Напри­мер, сокращение продолжительности проекта на 10 недель озна­чает сокращение накладных расходов второго типа на 15 тыс. долл.

Прибыль строительной компании оценивается в размере 10% от стоимости контракта. В стоимость контракта включаются пря­мые затраты на выполнение работ, премиальные и штрафные санк­ции и накладные расходы двух типов.

Задания

1. Нарисуйте сетевой график проекта, найдите критический путь и общую стоимость контракта при нормальной продол­жительности работ.

2. Определите продолжительность выполнения проекта, при которой прибыль строительной компании оказывается мак­симальной. Сроки выполнения каких работ следует сокра­тить по сравнению с нормальными?

3. Ответьте на вопросы предыдущего пункта, если при опре­делении стоимости контракта не учитываются накладные расходы второго типа.

4. Определите, за какое минимальное время можно выполнить проект.

Ответы и решения

Ответы на вопросы:1—3, 2 — 3, 3 — 1, 4 — 2, 5 — 5.

Задача 1. Решение.

Найдем критический путь при нормальном времени выполнения работ. Ис­пользуем для этого метод СРМ.

Введем в программу POMWIN исходную информацию, описывающую проект в виде последовательности работ:

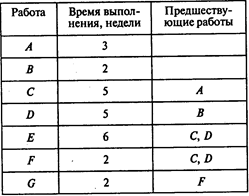
Выполнив расчеты, получаем следующие результаты:

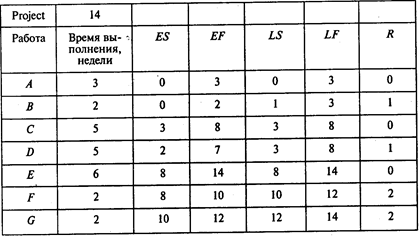
Отсюда видно, что при нормальной продолжительности работ длина крити­ческого пути составляет 14 недель. На критическом пути находятся работы А, С,Е.

Для того чтобы определить затраты на выполнение проекта при нормальной продолжительности работ, достаточно просуммировать затраты, указанные в пя­том столбце таблицы исходных данных, — в результате получаем 8400 тыс. руб.

Чтобы определить минимальные дополнительные издержки на сокращение продолжительности проекта до 10 недель, построим модель линейного програм­мирования. Для этого на основании данных о непосредственно предшествующих работах построим графическое представление проекта (рис. 4).

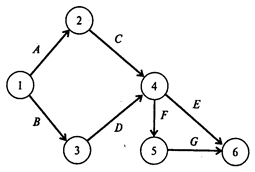
Рис. 4

Используя исходные данные, определяем удельные затраты К_ij на сокращение продолжительности работ. Получаем следующие результаты:

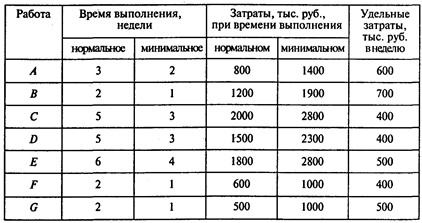
Используя обозначения x_i — время наступления события i; у_ij — величина со­кращения времени работы (i, j), получаем следующую модель линейного програм­мирования для определения минимальных издержек на сокращение продолжи­тельности проекта с 14 до 10 недель:

при условиях

Для решения этой задачи используем программу POMWIN:

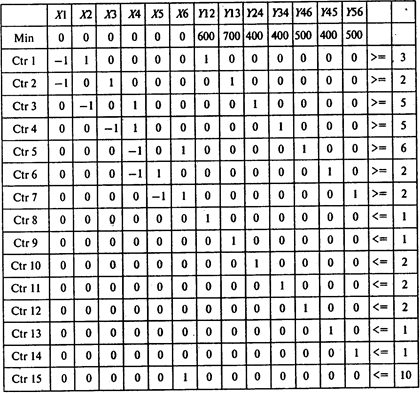
Выполнив расчеты, получаем следующие результаты:

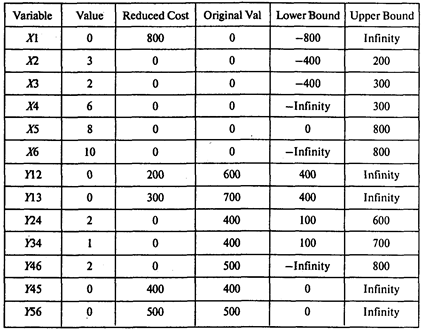
Итак, минимальные затраты на сокращение продолжительности проекта с 14 до 10 недель составляют 2200 тыс. руб. Продолжительность работ (2, 4) и (4, 6) сокращается на 2 недели. Продолжительность работы (3, 4) сокращается па не­делю.

Ответы: 1. 14 недель. 2. 8400 тыс. руб. 3. 6200 тыс. руб. 4. Для трех работ.

Задача 2. Решение.

Найдем критический путь при нормальном времени выполнения работ. Ис­пользуем для этого метод СРМ.

Введем в программу POMWIN исходную информацию, описывающую проект в виде последовательности работ:

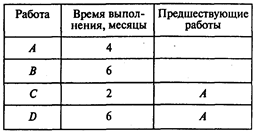
Окончание таблицы

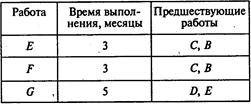
Выполнив расчеты, получаем следующие результаты:

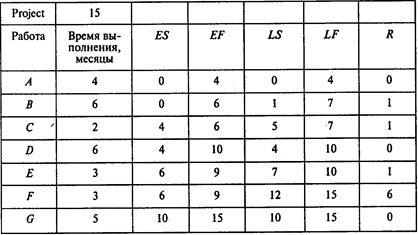
Отсюда видно, что при нормальной продолжительности работ длина крити­ческого пути составляет 15 месяцев. На критическом пути находятся работы А, D, С. Для того чтобы определить затраты на выполнение проекта при нормаль­ной продолжительности работ, достаточно просуммировать затраты, указанные в пятом столбце таблицы исходных данных, — в результате получаем 345 тыс. руб.

Чтобы определить минимальные дополнительные издержки на сокращение продолжительности проекта до 12 месяцев, построим модель линейного програм­мирования. Для этого на основании данных о непосредственно предшествующих работах построим графическое представление проекта (рис. 5).

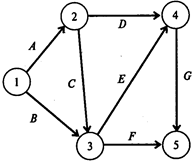
Рис.5

Используя исходные данные, определяем удельные затраты К_ij на сокращение продолжительности работ. Получаем следующие результаты:

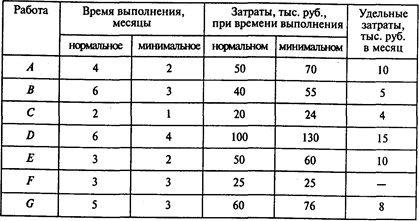
Используя обозначения хi — время наступления события i; у_ij — величина сокращения времени работы (i,j), получаем следующую модель линейного про­граммирования для определения минимальных издержек на сокращение продол­жительности проекта с 15 до 12 месяцев:

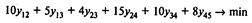
при условиях

Для решения этой задачи используем программу POMWIN:

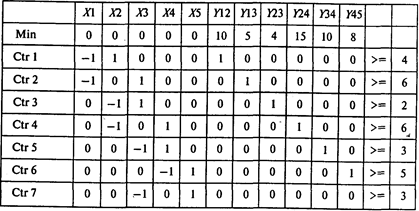
Окончание таблицы

Выполнив расчеты, получаем следующие результаты:

Итак, минимальные затраты, необходимые для того, чтобы сократить продол­жительность проекта с 15 до 12 месяцев, составляют 26 тыс. руб.

Продолжительность работы (1,2) сокращается на месяц.

Продолжительность работы (4, 5) сокращается на 2 месяца.

Определим, за какое минимальное время может быть выполнен проект

Для этого используем следующую модель линейного программирования:

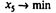
при условиях

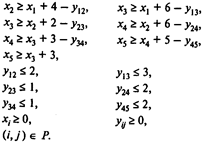
Для решения этой задачи используем программу POMWIN:

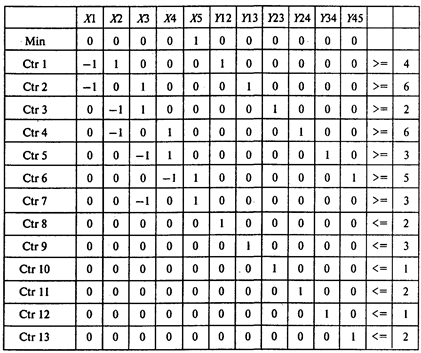
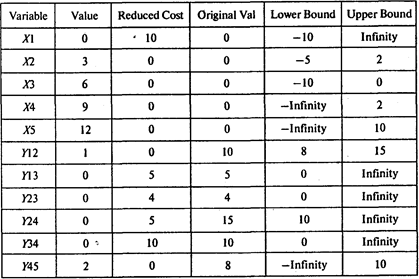
Выполнив расчеты, получаем следующие результаты:

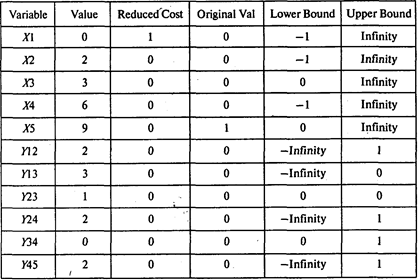
Следовательно, минимальная продолжительность проекта равна 9 месяцам. Для того чтобы сократить продолжительность проекта до 9 месяцев, продолжитель­ность работ (1, 2), (2, 4) и (4, 5) следует сократить на 2 месяца, работы (1, 3) — на 3, а работы (2, 3) — на месяц.

Ответы: 1. 15 месяцев. 2. 345 тыс. руб. 3. 319 тыс. руб. 4. За девять месяцев.

Задача 3. Решение.

Найдем критический путь при нормальном времени выполнения работ. Ис­пользуем для этого метод СРМ.

Введем в программу POMWIN исходную информацию, описывающую проект в виде последовательности работ:

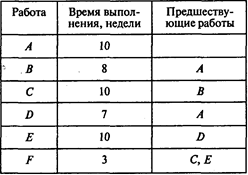
Выполнив расчеты, получаем следующие результаты:

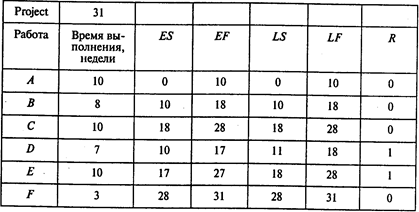
Отсюда видно, что при нормальной продолжительности работ длина крити­ческого пути составляет 31 неделю. На критическом пути находятся работы А, В, С, F.

Для того чтобы определить затраты на выполнение проекта при нормальной продолжительности работ, достаточно просуммировать затраты, указанные в шес­том столбце таблицы исходных данных, — в результате получаем 400 тыс. руб.

Чтобы определить минимальные дополнительные издержки на сокращение продолжительности проекта до 26 недель, построим модель линейного програм­мирования. Для этого на основании данных о непосредственно предшествующих работах построим графическое представление проекта (рис. 6).

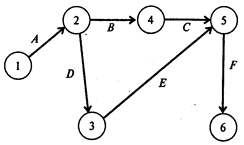
Рис. 6

Используя исходные данные, определяем удельные затраты К_ij на сокращение продолжительности работ. Получаем следующие результаты:

Используя обозначения х_i — время наступления события i; y_ij — величина сокращения времени работы (i,j), получаем следующую модель линейного про­граммирования для определения минимальных издержек на сокращение продол­жительности проекта с 31 до 26 недель:

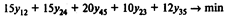
при условиях

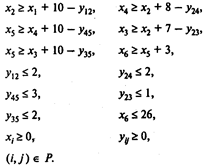
Для решения этой задачи используем программу POMWIN:

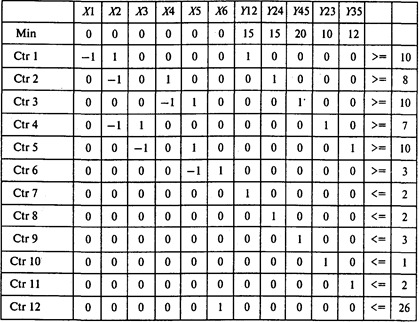
Выполнив расчеты, получаем следующие результаты:

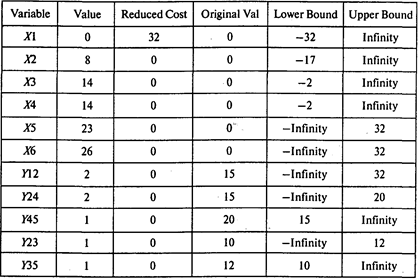
Итак, минимальные затраты на сокращение продолжительности проекта с 31 до 26 недель составляют 102 тыс. руб. Продолжительность работ (1, 2) и (2, 4) сокращается на 2 недели, работ (4, 5), (2, 3) и (3, 5) — на неделю.

Определим, за какое минимальное время может быть выполнен проект. Для этого используем следующую модель линейного программирования:

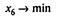
при условиях

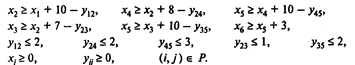
Для решения этой задачи используем программу POMWIN:

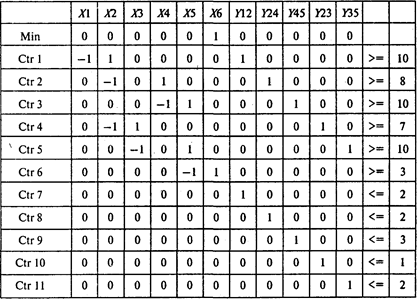
Выполнив расчеты, получаем следующие результаты:

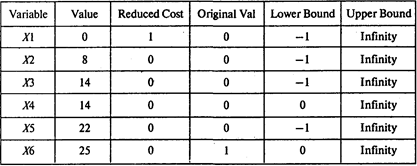
Окончание таблицы

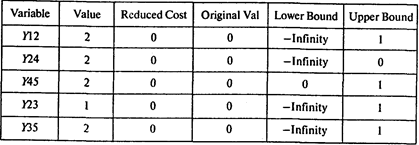
Следовательно, минимальная продолжительность проекта равна 25 неделям. Для того чтобы сократить продолжительность проекта с 31 до 25 недель, продол­жительность работ (1, 2), (2, 4), (4, 5) и (3, 5) следует сократить на 2 недели, ра­боты (2, 3) — на неделю.

Ответы: 1.31 неделя. 2. 400 тыс. руб. 3. 502 тыс. руб. 4. За 25 недель.

Задача 4. Решение.

Определим минимальное время выполнения проекта. Найдем критический путь, воспользовавшись методом СРМ.

Введем в программу POMWIN информацию о предшествующих работах и времени их выполнения:

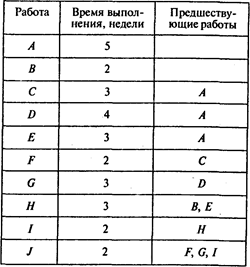
Результаты расчетов представлены в следующей таблице:

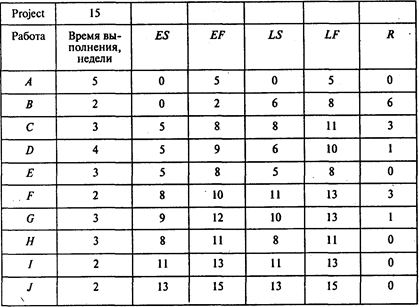
Ожидаемое время выполнения проекта — 15 недель.

Суммируя затраты на выполнение всех работ проекта, указанные в пятом столб­це таблицы исходных данных, получаем 313 тыс. руб.:

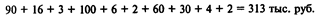
Определим удельные затраты на выполнение работ:

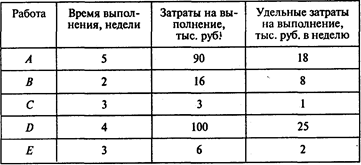
Окончание таблицы

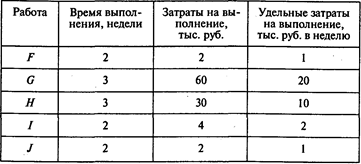
Определим динамику роста совокупных затрат для наиболее раннего време­ни начала всех работ:

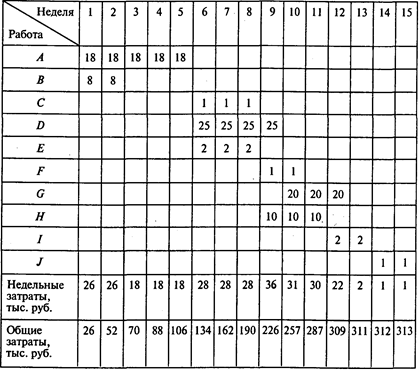
Определим динамику роста совокупных затрат для наиболее позднего време­ни начала всех работ:

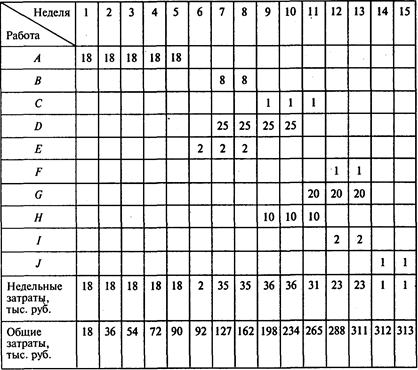
Проведеманализ фактических затрат.

Если в конце пятой недели фактические затраты будут находиться в интер­вале от 90 тыс. до 106 тыс. руб., то проект может быть выполнен за 15 недель. Фактические затраты на конец пятой недели составляют 100 тыс. руб. и удов­летворяют этому условию. Недостатка или перерасхода средств на этот момент времени нет.

Если в конце десятой недели фактические затраты будут находиться в интер­вале от 234 тыс. до 257 тыс. руб., то проект может быть выполнен за 15 недель. Фактические затраты на конец десятой недели составляют 230 тыс. руб. Это означает, что недостаток средств на конец десятой недели составляет 4 тыс. руб. и время выполнения проекта может возрасти.

Ответы: 1. 15 недель. 2. 106 тыс. руб. 3. 90 тыс. руб. 4. Недостатка или перерасхода средств в конце пятой недели нет. 5. 4 тыс. руб.

Задача 5. Решение.

Определим минимальное время выполнения проекта. Найдем критический путь, воспользовавшись методом СРМ.

Введем в программу POMWIN информацию о проекте, содержащуюся в пер­вом, втором и третьем столбцах таблицы исходных данных.

Результаты расчетов представлены в следующей таблице:

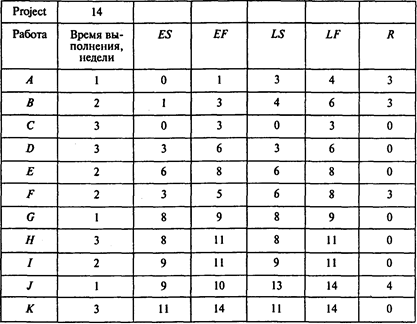
Ожидаемое время выполнения проекта — 14 недель. Суммируя затраты на выполнение всех работ проекта, получаем 124 тыс. руб.

Определим удельные затраты на выполнение работ:

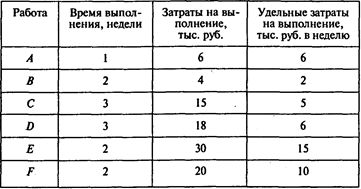
Окончание таблицы

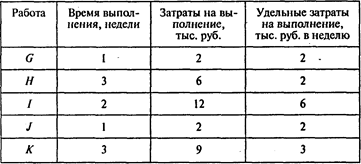
Определим динамику роста совокупных затрат для наиболее раннего време­ни начала всех работ:

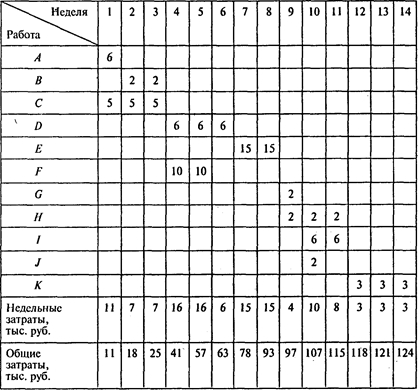
Определим динамику роста совокупных затрат для наиболее позднего време­ни начала всех работ:

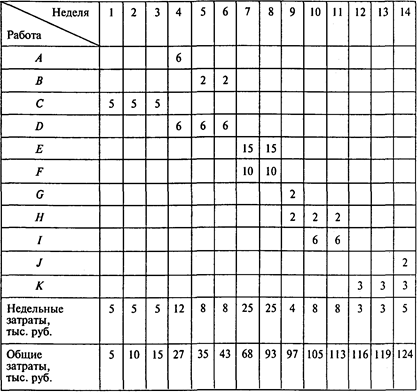
Проведем анализ фактических затрат.

Если в конце четвертой недели фактические затраты будут находиться в ин­тервале от 27 тыс. до 41 тыс. руб., то проект может быть выполнен за 14 недель. Фактические затраты на конец четвертой недели составляют 35 тыс. руб. и удов­летворяют этому условию. Недостатка или перерасхода средств на этот момент времени нет.

Для того чтобы проект был выполнен за 14 недель, фактические затраты в конце восьмой недели должны равняться 93 тыс. руб. Так как они равны 90 тыс. руб., то на конец восьмой недели имеет место недостаток средств 3 тыс. руб. и время вы­полнения проекта может возрасти.

Ответы: 1.14 недель. 2. 41 тыс. руб. 3. 27 тыс. руб. 4. Недостатка или перерасхода средств в конце четвертой недели нет. 5. 3 тыс. руб.

Глава 10. Стратегические игры

Цели

В данной главе показаны возможности использования одного из классов игровых моделей — так называемых стратегических игр — для принятия решений преимущественно экономического ха­рактера в условиях неопределенности. Дается общее описание страте­гической игры и ее место в классификации игр. Подробно рас­сматривается класс стратегических игр двух лиц с нулевой, а также с постоянной ненулевой суммой. Определяется понятие равнове­сия в ифе в чистых и смешанных стратегиях. Представлен общий подход к играм указанного типа — сведение к соответствующей задаче линейного программирования.

После того как вы выполните предлагаемые в этой главе зада­ния, вы будете уметь строить для различных ситуаций принятия экономических решений (там, где это возможно и целесообраз­но) соответствующую игровую модель, определяя:

• игроков и их стратегии;

• матрицу выигрышей;

• наличие или отсутствие седловых точек в чистых стратегиях;

• доминируемые стратегии;

• эквивалентную модель линейного программирования;

• оптимальные стратегии;

• цену игры.

Модели

Методы, основанные на теории игр, используются для приня­тия решений в условиях неопределенности. Игра — это матема­тическая модель конфликтной ситуации, которая предполагает на­личие следующих компонентов:

а) заинтересованных сторон;

б) возможных действий каждой из сторон;

в) интересов сторон.

В игре заинтересованные стороны называются игроками, каж­дый из которых может предпринимать не менее двух действий (если ифок имеет в своем распоряжении только одно действие, то он фактически не участвует в игре, поскольку заранее извест­но, что он предпримет).

Слово «игра» обозначает некоторый набор правил и соглаше­ний, составляющих данный вид игры, например: футбол, шахма­ты и др.

В экономике модель поведения лиц в виде игры возникает, например, при попытке нескольких фирм завоевать наиболее вы­годное место на конкурентном рынке или при желании несколь­ких лиц (компаний) разделить некоторое количество продукта (ресурса, финансовых средств) между собой так, чтобы каждому досталось как можно больше. Игроками в конфликтных эконо­мических ситуациях, моделируемых в виде игры, являются про­изводственные и непроизводственные фирмы, банки, отдельные предприниматели и другие экономические агенты. В военной области модель игры используется, например, для наилучшего выбора средств (из имеющихся или потенциально возможных) поражения военных целей противника или защиты от его напа­дения.

Для игр характерна неопределенность результата (исхода). При­чины неопределенности относятся к трем группам:

1) комбинаторные источники (шахматы);

2) влияние случайных факторов (игра в орлянку, кости, кар­точные игры, где случаен расклад);

3) стратегическое происхождение: игрок не знает, какого об­раза действий придерживается его противник. Здесь неопределен­ность исходит от другого лица.

Игры, в которых неопределенность имеет стратегическое проис­хождение, называются стратегическими.

Таким образом, в стратегической игре действия предпринима­ют две стороны или более, в отличие от нестратегической игры, в которой действия предпринимает одна сторона, а остальные яв­ляются заинтересованными сторонами.

Стратегические игры классифицируют по следующим при­знакам:

1) число игроков (игра двух лиц, игра п (п > 2) лиц);

2) количество стратегий (конечные, бесконечные);

3) количество информации, имеющейся у игроков относитель­но прошлых ходов (игры с полной, игры с неполной информаци­ей). Шахматы — пример игры с полной информацией;

4) принцип деления выигрыша (коалиционные, бескоалици­онные).

Далее рассматривается модель конечной стратегической игры с полной информацией, в которой участвуют две стороны, име­ющие противоположные интересы. Такую игру принято называть конечной игрой двух лиц с нулевой суммой.