Простейшая модель оптимального размера заказа.

Предположим, что:

1) темп спроса на товар известен и постоянен;

2) получение заказа мгновенно;

3) закупочная цена не зависит от размера заказа;

4) дефицит не допускается.

Исходные данные: темп спроса, издержки заказа, издержки хра­нения.

Результат: оптимальный размер заказа, время между заказа­ми, количество заказов за фиксированный период времени, сово­купные издержки.

Размер заказа является постоянным. Заказ выполняется мгно­венно. Уровень запасов убывает с постоянной интенсивностью, пока не достигает нулевого значения. В этот момент времени де­лается и мгновенно выполняется заказ и уровень запаса восста­навливается до максимального значения. При этом оптимальным решением задачи будет такой размер заказа, при котором миними­зируются общие издержки за период, равные сумме издержек хра­нения и издержек заказа.

Динамика изменения количества продукта s на складе показа­на на рис. 1.

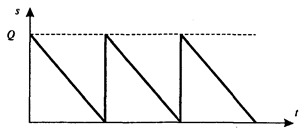
Рис. 1

Пусть Q — размер заказа;

Т — продолжительность периода планирования;

D, d — величина спроса за период планирования и в еди­ницу времени соответственно;

К — издержки одного заказа;

Н, h — удельные издержки хранения за период и в еди­ницу времени соответственно.

Тогда:

Кривые издержек заказа С₁ издержек хранения С₂ и совокуп­ных издержек С показаны на рис. 2.

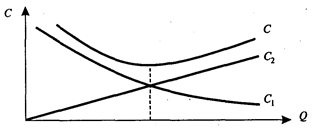
Рис.2

Определив минимум функции совокупных издержек, получаем:

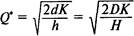— оптимальный размер заказа;

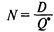— оптимальное число заказов за период;

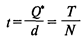— время цикла (оптимальное время между заказами).

Следует обратить внимание на то, что оптимальный размер заказа не зависит от цены продукта.