Індивідуальне завдання №1 3 страница
Зауваження. Коефіцієнт детермінації 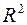 є сенс розглядати тільки у випадку наявності вільного члена в моделі (2.2), тобто
є сенс розглядати тільки у випадку наявності вільного члена в моделі (2.2), тобто 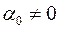 , оскільки тільки у цьому випадку, як це вище відзначалося, виконується рівність (2.42), а, отже, і співвідношення (2.46*).
, оскільки тільки у цьому випадку, як це вище відзначалося, виконується рівність (2.42), а, отже, і співвідношення (2.46*).
Зміст 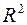 нагадує зміст вибіркового коефіцієнта кореляції
нагадує зміст вибіркового коефіцієнта кореляції 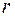 . Це обумовлено рівністю
. Це обумовлено рівністю
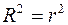 , (2.47)
, (2.47)
яка отримується із використанням (2.46), (1.20), (2.13):
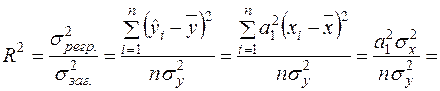
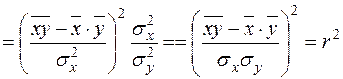 .
.
Числові характеристики 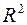 та
та 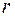 є точковими статистичними оцінками відповідних невідомих чисел. У зв’язку із цим навіть у випадку
є точковими статистичними оцінками відповідних невідомих чисел. У зв’язку із цим навіть у випадку 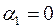
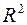 та
та 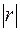 можуть бути відмінними від нуля. А тому виникає необхідність перевірити значущість
можуть бути відмінними від нуля. А тому виникає необхідність перевірити значущість 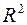 та
та 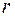 , отриманих для конкретної вибірки.
, отриманих для конкретної вибірки.
Якщо 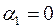 , тобто відсутня лінійна залежність між залежною і пояснюючою змінними, тоді випадкові величини
, тобто відсутня лінійна залежність між залежною і пояснюючою змінними, тоді випадкові величини
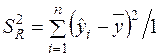 та
та 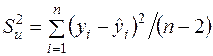
мають 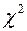 -розподіли відповідно із 1 та
-розподіли відповідно із 1 та 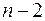 ступенями вільності, а їх відношення (згідно із (1.15)) — розподіл Фішера з тими ж ступенями вільності. Тому рівняння регресії значуще на рівні значущості
ступенями вільності, а їх відношення (згідно із (1.15)) — розподіл Фішера з тими ж ступенями вільності. Тому рівняння регресії значуще на рівні значущості 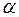 , якщо виконується нерівність
, якщо виконується нерівність
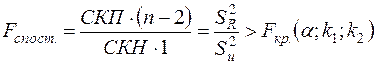 , (2.48)
, (2.48)
де 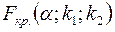 — табличне значення
— табличне значення 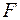 -критерія Фішера-Снедокора, визначене на рівні значущості
-критерія Фішера-Снедокора, визначене на рівні значущості 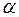 при
при 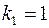 і
і 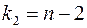 ступенях вільності.
ступенях вільності.
Проте виявляється [8, с.97], що 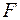 -тест (2.48) рівносильний
-тест (2.48) рівносильний 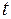 -тесту Ст’юдента при перевірці значущості параметра
-тесту Ст’юдента при перевірці значущості параметра 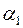 (у випадку парної лінійної моделі).
(у випадку парної лінійної моделі).
В ряді задач потрібно оцінити значущість коефіцієнта кореляції 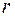 . На рівні значущості
. На рівні значущості 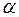 він вважається значущим (тобто відкидається гіпотеза
він вважається значущим (тобто відкидається гіпотеза 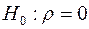 ), якщо виконується нерівність (1.21). Однак неважко показати, що отримувані значення
), якщо виконується нерівність (1.21). Однак неважко показати, що отримувані значення 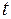 -критерію при перевірці гіпотез
-критерію при перевірці гіпотез 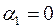 по (2.33) і
по (2.33) і 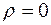 по (1.21) однакові.
по (1.21) однакові.
Отже, якщо на рівні 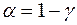 зроблено висновок про значущість
зроблено висновок про значущість 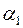 , то на тому ж рівні вважається значущим і генеральний (теоретичний) коефіцієнт кореляції
, то на тому ж рівні вважається значущим і генеральний (теоретичний) коефіцієнт кореляції 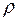 і навпаки.
і навпаки.
Наведемо інші прості показники якості лінійної регресії, які використовуються як додаткова інформація при виборі найкращої моделі з можливих.
Абсолютна середня відсоткова помилка МАРЕ (mean absolute percentage error):
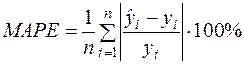 . (2.49)
. (2.49)
Цей показник використовується при порівнянні точності прогнозів різнорідних об’єктів, бо характеризує відносну точність прогнозу. При цьому вважається, що значення МАРЕ, менше 10%, дає високу точність прогнозу, а, отже, і якість моделі; від 10% до 20% — добру точність; від 20% до 50% — задовільну точність; понад 50% — незадовільну точність.
Середня відсоткова помилка МРЕ (mean percentage error):
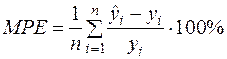 . (2.50)
. (2.50)
Це показник незміщеності прогнозу. З точки зору практики для якісних моделей цей показник повинен бути «малим», тобто не перевищувати 5%.
Зауваження. Показники (2.49) та (2.50) — невизначені, якщо серед 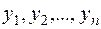 є нульове значення.
є нульове значення.
10. Якщо встановлено, що побудована модель є адекватною, тоді можна знаходити прогнозні значення залежної змінної. При цьому можна отримати два типи прогнозів: точковий та інтервальний. Нехай задається значення 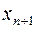 незалежної змінної. Тоді точковий прогноз для значення залежної змінної за моделлю (2.11) має такий вигляд:
незалежної змінної. Тоді точковий прогноз для значення залежної змінної за моделлю (2.11) має такий вигляд:
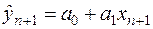 . (2.51)
. (2.51)
Разом з тим дійсне значення залежної змінної для прогнозного періоду згідно із (2.3) дорівнює:
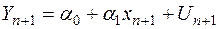 , (2.52)
, (2.52)
де стосовно випадкової величини 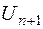 природно вимагати виконання передумов 1-4, тобто
природно вимагати виконання передумов 1-4, тобто
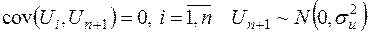 . (2.53)
. (2.53)
Отже, 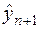 є точковою оцінкою невідомого числа
є точковою оцінкою невідомого числа 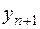 , яке є реалізацією (можливим значенням) випадкової величини (2.52).
, яке є реалізацією (можливим значенням) випадкової величини (2.52).
Згідно із (2.51), (2.52) помилка прогнозу:
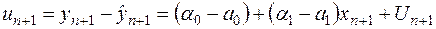 . (2.54)
. (2.54)
Потрібно знайти числові характеристики 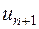 та закон розподілу. Незміщеність оцінок
та закон розподілу. Незміщеність оцінок 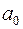 ,
, 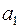 і (2.53) призводять до рівності
і (2.53) призводять до рівності 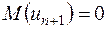 . Оскільки
. Оскільки 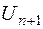 не корелює із
не корелює із 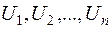 , то згідно із (2.3)
, то згідно із (2.3) 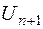 не корелює і з
не корелює і з 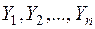 . Тому із врахуванням детермінованості
. Тому із врахуванням детермінованості 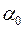 ,
, 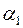 ,
, 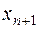 , (2.14), (2.18), (2.19) отримаємо:
, (2.14), (2.18), (2.19) отримаємо:
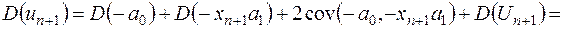
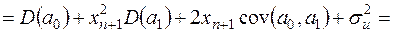
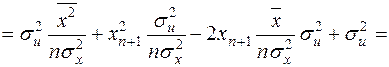
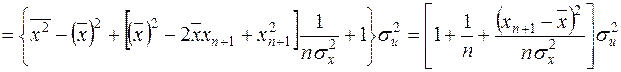 .
.
Неважко переконатися також у лінійній залежності 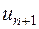 від збурень
від збурень 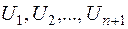 . А тому остаточно отримуємо:
. А тому остаточно отримуємо:
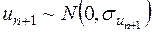 ,
,
де
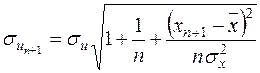 .
.
Незміщена оцінка 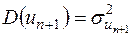 знаходиться за формулою
знаходиться за формулою
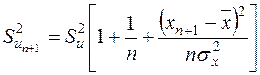 , (2.55)
, (2.55)
де 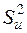 визначена формулою (2.22).
визначена формулою (2.22).
За аналогією із побудовою інтервальної зони функції регресії (п.7) остаточно можна отримати довірчий інтервал для прогнозного значення залежної змінної:
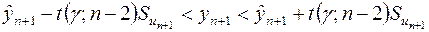 . (2.56)
. (2.56)
11. Задача 2.1. Торгівельне підприємство має велику кількість філій і його керівництво вивчає питання про залежність 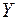 (річний товарообіг однієї філії, млн. грн.) від
(річний товарообіг однієї філії, млн. грн.) від 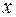 (торгівельної площі, тис. м2). Для десяти філій за певний рік зафіксовані такі значення показників
(торгівельної площі, тис. м2). Для десяти філій за певний рік зафіксовані такі значення показників 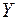 і
і 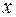 :
:
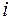
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
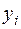
| 1,5 | 2,9 | 3,1 | 3,2 | 4,3 | 5,7 | 5,8 | 7,2 | 7,5 | |
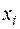
| 0,2 | 0,3 | 0,5 | 0,6 | 0,8 | 1,1 | 1,2 | 1,3 | 1,4 |
На обсяг товарообігу впливають такі чинники: середньоденна інтенсивність потоку покупців, об’єм основних фондів, їх структура, середньоспискова чисельність працівників, площа підсобних приміщень тощо. Припускається, що в досліджуваній групі філій значення цих чинників приблизно однакові, тому вплив відмінностей їх значень на зміну обсягу товарообігу є незначним.
Вважаючи, що виконуються передумови 1-4, потрібно:
1) знайти статистичні оцінки параметрів лінійного рівняння регресії;
2) точкову оцінку та довірчий інтервал дисперсії збурень із надійністю 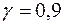 ;
;
3) для рівня значущості 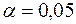 перевірити значущість коефіцієнтів регресії
перевірити значущість коефіцієнтів регресії 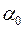 та
та 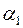 ;
;
4) знайти довірчі інтервали коефіцієнтів регресії з надійністю 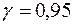 ;
;
5) знайти вибіркові коефіцієнт детермінації, коефіцієнт кореляції, а також інші показники якості лінійної регресії (МАРЕ, МРЕ);
6) знайти та побудувати довірчу зону функції регресії з надійністю 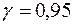 ;
;
7) знайти прогнозне значення річного товарообігу для нової філії, торгівельна площа якої складає 1,8 тис. м2, а також із надійністю 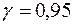 побудувати довірчий інтервал для цього прогнозного значення.
побудувати довірчий інтервал для цього прогнозного значення.
¡ 1) Статистичні оцінки 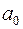 ,
, 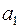 параметрів
параметрів 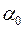 та
та 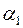 лінійного рівняння регресії задовольняють системі нормальних рівнянь (2.12):
лінійного рівняння регресії задовольняють системі нормальних рівнянь (2.12):
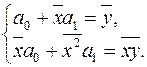
Для знаходження коефіцієнтів цієї системи складемо розрахункову табл. 2.1, останній стовпець якої потрібний для обчислення 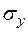 .
.
Таблиця 2.1
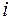
| 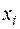
| 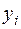
| 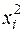
| 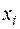 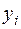
| 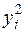
|
| 1 | 0,2 | 1,5 | 0,04 | 0,3 | 2,25 |
| 2 | 0,3 | 2,9 | 0,09 | 0,87 | 8,41 |
| 3 | 0,5 | 3,1 | 0,25 | 1,55 | 9,61 |
| 4 | 0,6 | 3,2 | 0,36 | 1,92 | 10,24 |
| 5 | 0,8 | 4,3 | 0,64 | 3,44 | 18,49 |
| 6 | 5,7 | 5,7 | 32,49 | ||
| 7 | 1,1 | 5,8 | 1,21 | 6,38 | 33,64 |
| 8 | 1,2 | 1,44 | 8,4 | ||
| 9 | 1,3 | 7,2 | 1,69 | 9,36 | 51,84 |
| 10 | 1,4 | 7,5 | 1,96 | 10,5 | 56,25 |
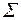
| 8,4 | 48,2 | 8,68 | 48,42 | 272,22 |
Використовуючи нижній рядок табл. 2.1, отримаємо (обсяг вибірки 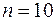 ):
):
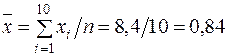 ;
; 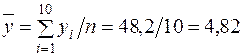 ;
;
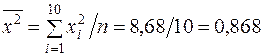 ;
; 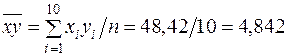 ;
;
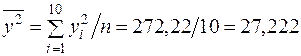 ;
;
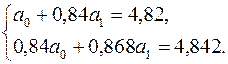
Єдиний розв’язок цієї системи рівнянь згідно із формулами (2.13):
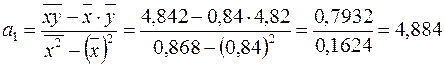 ,
,
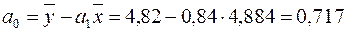 .
.
Отже, емпіричне рівняння регресії має такий вигляд:
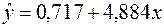 . (2.57)
. (2.57)
2) Незміщену точкову оцінку 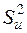 невідомої дисперсії збурень
невідомої дисперсії збурень 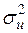 знайдемо за формулою (2.22):
знайдемо за формулою (2.22):
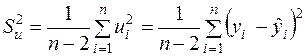 ,
,
попередньо обчисливши 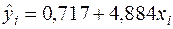 та
та 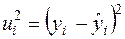 ,
,  , (табл. 2.2).
, (табл. 2.2).
Таблиця 2.2
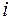
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 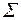
|
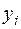
| 1,5 | 2,9 | 3,1 | 3,2 | 4,3 | 5,7 | 5,8 | 7,2 | 7,5 | – | |
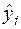
| 1,6938 | 2,1822 | 3,159 | 3,6474 | 4,6242 | 5,601 | 6,0894 | 6,5778 | 7,0662 | 7,5546 | – |
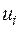
| -0,1938 | 0,7178 | -0,059 | -0,4474 | -0,3242 | 0,099 | -0,2894 | 0,4222 | 0,1338 | -0,0546 | 0,0044 |
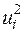
| 0,0376 | 0,5152 | 0,0035 | 0,2002 | 0,1051 | 0,0098 | 0,0838 | 0,1783 | 0,0179 | 0,003 | 1,1544 |
Зауваження. Згідно із (2.21): 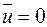 , в той час як у нашому випадку
, в той час як у нашому випадку 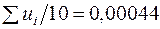 . Цим значенням можна ігнорувати (вважати практично рівним нулю). Разом з тим з’ясуємо причину такого відхилення від нуля. Значення
. Цим значенням можна ігнорувати (вважати практично рівним нулю). Разом з тим з’ясуємо причину такого відхилення від нуля. Значення 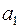 та
та 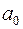 з точністю до шести знаків після коми відповідно складають 4,884236 та 0,717242, тобто обидва ці значення (хай і несуттєво) більші тих, які взяті у моделі (2.57). Накопичення додатних похибок у різницях
з точністю до шести знаків після коми відповідно складають 4,884236 та 0,717242, тобто обидва ці значення (хай і несуттєво) більші тих, які взяті у моделі (2.57). Накопичення додатних похибок у різницях 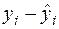 і привело до того, що
і привело до того, що 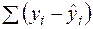 незначно перевищує нуль. Відмітимо також, що значення
незначно перевищує нуль. Відмітимо також, що значення 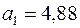 ,
, 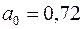 приводять до рівності
приводять до рівності 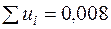 .
.
Використавши підсумок останнього рядка, отримаємо:
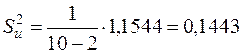 .
.
Ліва і права межі довірчого інтервалу для 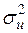 визначаються згідно (2.29) за формулами відповідно
визначаються згідно (2.29) за формулами відповідно 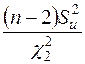 і
і 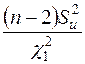 , де у відповідності із (2.26) та (2.27)
, де у відповідності із (2.26) та (2.27) 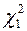 та
та 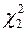 є коренями рівнянь
є коренями рівнянь
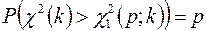 ,
, 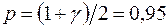 ,
,
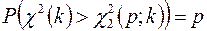 ,
, 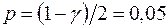 .
.
За табл. 4 додатків для 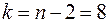 знайдемо:
знайдемо: 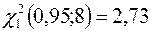 і
і 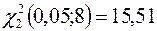 . Тоді ліва межа довірчого інтервалу дорівнює
. Тоді ліва межа довірчого інтервалу дорівнює 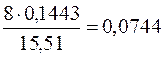 , а права —
, а права — 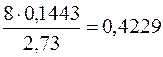 . Тобто остаточно з надійністю 0,9
. Тобто остаточно з надійністю 0,9
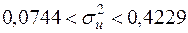 .
.
3) Згідно з п.8, якщо виконується нерівність (2.33): 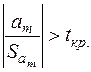
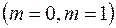 , тоді на рівні значущості
, тоді на рівні значущості 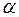 приймається гіпотеза
приймається гіпотеза 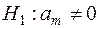 . Значення
. Значення 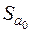 та
та 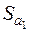 знайдемо із виразів (2.30):
знайдемо із виразів (2.30):
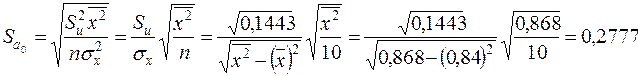 ;
;
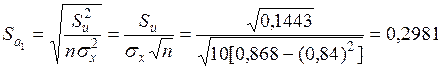 .
.
Тоді спостережені значення критерію:
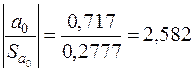 ,
, 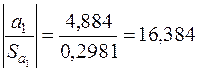 .
.
Критична точка для двосторонньої критичної області 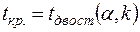 при значеннях
при значеннях 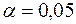 ,
, 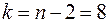 знаходиться за верхньою частиною табл. 3 додатків:
знаходиться за верхньою частиною табл. 3 додатків: 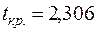 .
.
Оскільки 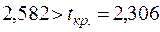 і
і 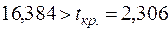 , то на рівні значущості
, то на рівні значущості 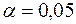 робимо висновки, що
робимо висновки, що 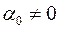 і
і 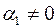 .
.
4) Згідно з (2.39) та (2.40) довірчі інтервали з надійністю 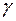 для невідомих параметрів регресії
для невідомих параметрів регресії 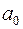 та
та 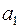 мають такий вигляд:
мають такий вигляд:
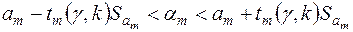 ,
,
де 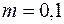 ,
, 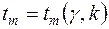 — корінь рівняння
— корінь рівняння 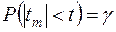 ,
, 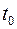 та
та 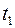 — випадкові величини, розподілені за законом Ст’юдента.
— випадкові величини, розподілені за законом Ст’юдента.
У нашому випадку 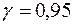 , число ступенів вільності
, число ступенів вільності 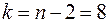 . За табл. 2 додатків знаходимо
. За табл. 2 додатків знаходимо 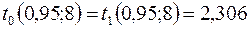 . Тоді з врахуванням знайдених значень
. Тоді з врахуванням знайдених значень 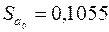 ,
, 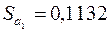 отримаємо:
отримаємо:
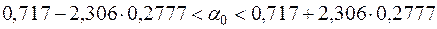 ,
,
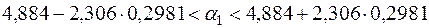
або остаточно
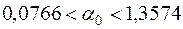 ,
,
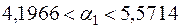 .
.
5) Коефіцієнт детермінації 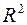 знайдемо за формулою (2.46*):
знайдемо за формулою (2.46*):
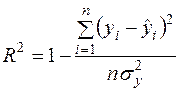 .
.
Із табл. 2.2 (останнє число нижнього рядка) 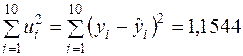 .
.
Для знаходження 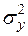 використаємо табл. 2.1:
використаємо табл. 2.1:
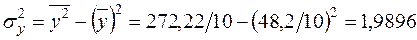 .
.
Отже,
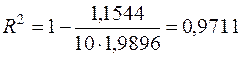 .
.
Таким чином, варіація залежної змінної 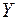 на 97,11% пояснюється варіацією пояснюючої змінної.
на 97,11% пояснюється варіацією пояснюючої змінної.
Вибірковий коефіцієнт кореляції згідно із (2.47):
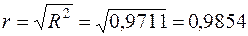 .
.
При цьому додатний знак цього числа обрано в зв’язку з тим, що 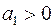 .
.
Обчислимо абсолютну середню відсоткову помилку МАРЕ за формулою (2.49):
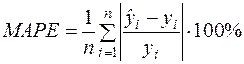 .
.
Для цього використаємо другий і четвертий рядки табл. 2.2:
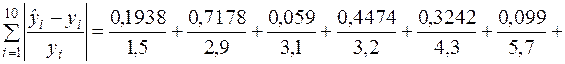
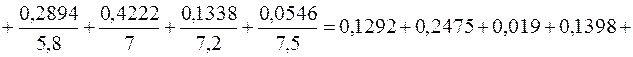
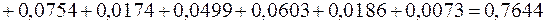 .
.
Отже, 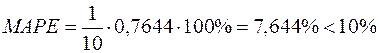 , тобто відповідає високій точності прогнозу за моделлю.
, тобто відповідає високій точності прогнозу за моделлю.
Середню відсоткову помилку МРЕ знайдемо за формулою (2.50):
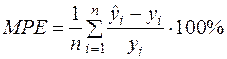 ,
,
використавши розрахунки при обчисленні МАРЕ:
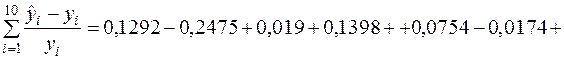
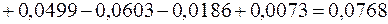 .
.
Остаточно
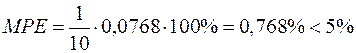 .
.
Висновок: всі знайдені показники вказують на високу якість моделі.
6) Побудова довірчої зони для функції регресії передбачає побудову точок з координатами 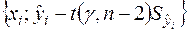 ,
,  , з наступним з’єднанням сусідніх (по індексу
, з наступним з’єднанням сусідніх (по індексу 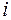 ) точок прямолінійними відрізками, а потім здійснення аналогічної процедури для послідовності точок
) точок прямолінійними відрізками, а потім здійснення аналогічної процедури для послідовності точок 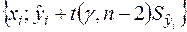 .
.
Дата добавления: 2016-06-13; просмотров: 1165;
